从 PixelCNN 到 Gated PixelCNN，再到 Conditional Gated PixelCNN

一、简介

PixelCNN 是一个生成模型，2016年出自DeepMind的Aaron van den Oord[1]。[5]指出当前的生成模型主要可分为两类：

• 基于最大似然的模型，比如：各类VAE（变分自编码器） 和 autoregressive models（自回归模型）
• 隐式生成模型，比如：Gan（生成对抗网络）

PixelCNN属于第一种模型，即最大似然模型。这种生成模型较Gan的优势是[5]：
likelihood based methods optimize negative log-likelihood (NLL) of the training data. This objective allows model-comparison and measuring generalization to unseen data. Additionally, since the probability that the model assigns to all examples in the training set is maximized, likelihood based models, in principle, cover all modes of the data, and do not suffer from the problems of mode collapse and lack of diversityseen in GANs.
简单说就是，Gan还很难进行模型的比较（即没有一个好的方法来比较各种Gan模型），它对于未见过的数据之泛化，不能覆盖真实数据的所有多样性，而且会出现模式坍塌和数据多样性的损失。而以上这些，在最大似然模型的方法中都可以解决，由此可见，Gan虽热却不是包打天下的，近期的[5]就生成了质量堪比BigGan[6]的图像。[5] 所使用的方法是一种复合方法，主要是两种方法的复合：一种是VQ-VAE（矢量量化-变分自编码），我在上一篇博客有介绍；另一种就是本篇博客介绍的PixelCNN。这两种似然方法的结合，也能创造出惊艳的作品来，而且不需要太多的资源，真是我等草根的福音，以下我就自己的理解来聊一聊PixelCNN。

二、PixelCNN

如果我们把一幅图片 $\mathbf{x}$ 看成是由各像素 $x_i$ 随机组成的随机变量 $\mathbf{x}=\{x_1,x_2,\cdots ,x_N\}$，则一幅图片就可以表示为各像素的联合分布：
$$p(\mathbf{x})=p(x_1,x_2,\cdots ,x_N)$$
PixelCNN 的基本思想是将这个联合分布因子化，用条件分布的乘积来表示，如下：
$$p(x_1,x_2,\cdots ,x_N)=\prod _{i=1}^{N}p(x_i|x_{<i})(1)$$
在生成这幅图片时，我们用前面的像素作为条件，作条件概率，估算当前的像素概率，逐点生成像素。这个思想其实也很朴素和直白，具体就是：

1. 由 $p(x_1)$ 得到 ${\hat{x}}_1$;
2. 由 $p(x_2|{\hat{x}}_1)$ 得到 ${\hat{x}}_2$;
3. 由 $p(x_3|{\hat{x}}_1{\hat{x}}_2)$ 得到 ${\hat{x}}_3$;
4. 循环往复，直到最后一个像素 $p(x_N|{\hat{x}}_1{\hat{x}}_2\cdots {\hat{x}}_{N-1})\to {\hat{x}}_N$
   如下图：
   
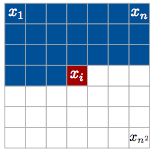
   图1 $x_i$ 条件概率示意图，它与之前的点有关（蓝色部分），与它之后的点无关（白色部分）

图像原本是二维矩阵（不同的 channel 先合起来看），将矩阵中元素排成一个序列，就可以应用上述的条件概率。序列的顺序可按扫描顺序，比如：从左到右-从上到下行扫描，或Z扫描。

那么还剩下一个问题就是，如何得到这一系列的条件概率：$p(x_i|x_{<i})$ ？
[1]想了个很好的方法，就是通过深度神经网络来进行函数拟合（或称为回归 Regresion）。要进行序列的预测，很自然就想到了 RNN 模型，[1]给出的第一个模型就是基于LSTM 的 PixelRNN 模型。该模型将像素 $x_i$ 逐一输入，即可在输出端获得 $p(x_i|x_{<i})$，其生成图像的质量要优于 PixelCNN，但它由于是串行模型，训练起来耗时极长，由于它不是本篇的重点，我们不做详细介绍。
[1] 中除了给出 PixelRNN 还给了一个并行模型 PixelCNN，该模型一次就可以将图像 $\mathbf{x}$ 的全部像素都并行输入，并在输出端得到与各像素相应的条件概率，如图：

图2 PixelCNN的并行性，并行输入$\{x_1,x_2,x_3\}$，并行产生$\{p(x_1),p(x_2|x_1),p(x_3|x_1{x}_2)\}$

PixelCNN利用了CNN的并行性，将模型学习的速度大大提升，但由于CNN的receptive field 的限制，以及CNN复杂度不如LSTM，因此其生成的效果不如PixelRNN。
PixelCNN 的实现比较简单，考虑到要用前面的像素估计后面像素的概率，因此在构建 CNN 时，需要应用一个模板，如下是一个 $5\times 5$ 的 mask：

图5 一个 $5\times 5$ 的模板
该模板与传统CNN filter 的 weight 逐元点积后，再做常规 convolution 操作，其简单实现代码可以参考[3]：

class MaskedConv2d(nn.Conv2d):
    def __init__(self, mask_type, *args, **kwargs):
        super(MaskedConv2d, self).__init__(*args, **kwargs)
        assert mask_type in {'A', 'B'}
        self.register_buffer('mask', self.weight.data.clone())
        _, _, kH, kW = self.weight.size()
        self.mask.fill_(1)
        self.mask[:, :, kH // 2, kW // 2 + (mask_type == 'B'):] = 0
        self.mask[:, :, kH // 2 + 1:] = 0

    def forward(self, x):
        self.weight.data *= self.mask
        return super(MaskedConv2d, self).forward(x)

MaskedConv2d 有两种，一种称为“A”，另一种为“B”，区别就是 filter 中间像素是否屏蔽，A型屏蔽，B型不屏蔽。在用 MaskedConv2d 构建模型时，一般是第一层用A型，其后均用B型，简单实现如下：

fm = 64
net = nn.Sequential(
    MaskedConv2d('A', 1,  fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    MaskedConv2d('B', fm, fm, 7, 1, 3, bias=False), nn.BatchNorm2d(fm), nn.ReLU(True),
    nn.Conv2d(fm, 256, 1))

由于模型输出的是概率值，因此在构建Loss时,可以采用交叉熵（cross_entropy）来衡量两个概率的差异，简单的实现如下：（完整代码见[3]）

for epoch in range(25):
    # train
    err_tr = []
    cuda.synchronize()
    time_tr = time.time()
    net.train(True)
    for input, _ in tr:
        input = Variable(input.cuda(async=True))
        target = Variable((input.data[:,0] * 255).long())
        loss = F.cross_entropy(net(input), target)
        err_tr.append(loss.data[0])
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

上一段代码中有： target = Variable((input.data[:,0] * 255).long())，是因为所选的数据集是MNIST，其图是二值图像，只有0、1，因此将其扩展至 [0，255] 上。
由于本网络实现简单，训练时间很快就可以结束，在获得了 trained model 后，我们需要逐点生成图像，在这一点上 PixelCNN 与 PixelRNN 并没有什么不同，简单的抽样代码如下：

#  sample
sample.fill_(0)
net.train(False)
for i in range(28):
   for j in range(28):
       out = net(Variable(sample, volatile=True))
       probs = F.softmax(out[:, :, i, j]).data
       sample[:, :, i, j] = torch.multinomial(probs, 1).float() / 255.
utils.save_image(sample, 'sample_{:02d}.png'.format(epoch), nrow=12, padding=0)

结果如下图：

图6 PixelCNN 的生成效果

三、Gated PixelCNN

前面讲过 PixelCNN 的生成效果不如 PixelRNN，[2] 凭直觉是因为两个原因：

• PixelRNN 在生成当前像素条件概率时，使用了所有之前所有的像素信息，而PixelCNN 受到 receptive field 的影响，只能从其中一部分相邻像素获得信息，而且还会受到 blind spot（盲点）的影响，盲点可以占到有效 receptive field 的四分之一，因而直接使用 PixelCNN 预测会受到信息不完整的影响；
• PixelRNN 的实现单元是 LSTM 其结构复杂，有多个选择的门（gate），因而其本身就可以对更复杂的关系进行建模，因而其建模能力要优于仅使用简单的 CNN 的PixelCNN 的能力。

有了这样的认识，就诞生了 Gated PixelCNN。我们先来看看盲点是如何产生的，如下图：

图7 盲点的产生，以及盲点的消除
由于在产生模型所需的 MaskCNN 时，掩住了当前像素同一行的右边像素（注意，模板中间像素为当前像素），当构建多层 MaskCNN 网络时，叠加效应使 receptive field 产生了盲点，图7中右边上部图示。为消除这个盲点，可将每一层的 receptive field 分为两个部分，这样每一部分都是规则的矩形：

• horizontal 部分，只是当前像素所在行，其模板如下：
  

• vertical 部分，是当前像素上方的掩码皆为1，其本行和下方行的掩码皆为0；
  这两个部分所处理的区域皆是规则矩形，不会产生盲点，它们分别处理后再合成，或送往下一层，如图7右边的下部。

另外，为了构造更复杂建模单元，Gated PixelCNN 用了一个与 attention 类似的机制——Gate（逐点乘），替换了原有的非线性激活单元，如： ReLU。这样就让单个 Gated PixelCNN 层具有了更强的复杂模型构建能力，其激活函数如下：
$$\mathbf{y}=\tanh (W_{k,f}\ast \mathbf{x})\odot \sigma (W_{k,g}\ast \mathbf{x})(2)$$
上式中 $\sigma (\cdot )$ 表示sigmoid函数，而 $\odot$ 表示按位乘积，我们来看看它的结构图：

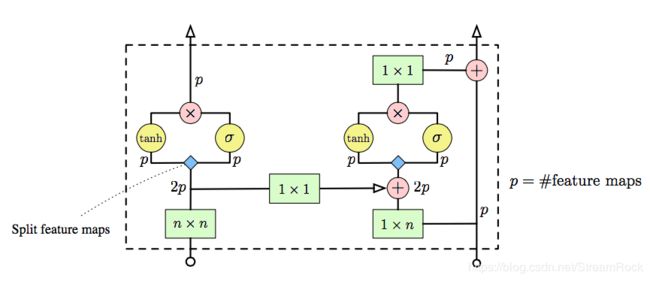
图8 Gated PixelCNN 结构示意图
图8中所示，输入分为两部分：左边是vertical部分，因此维度是 $n\times n$；右边输入是 horizontal 部分，因此是一行，即 $1\times n$；p 是feature maps的个数。在这个实现中，horizontal 部分处理加入了 Residual Connection，而在 vertical 部分没有加入，因为 [2] 在做实验时发现，加入了Residual Connection 也没有什么提升的效果，因此省了。将这样的 Gated PixelCNN 层叠起来，我们可以得到如下的模型：

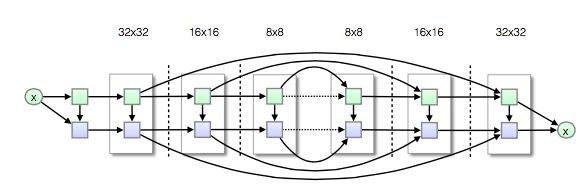
图9 堆叠的 Gated PixelCNN 模型。
在图9中，纵列的两个小矩形代表一个 Gated PixelCNN 处理单元，其中，绿色的代表 vertical 处理部分，蓝色的表示 horizontal 处理部分。
Gated PixelCNN 的代码略为复杂，具体可参考[4]。

四、Conditional Gated PixelCNN

Conditional Gated PixelCNN 是 Gated PixelCNN 的升级版，它在原来的条件模型中加入了条件 $\mathbf{h}$，使原来的条件概率变成了:
$$p(\mathbf{x}|\mathbf{h})=\prod _{i=1}^{n^2}p(x_i|x_1,\cdots ,x_{i-1},\mathbf{h})(3)$$
为什么要加入条件 $\mathbf{h}$ 呢？因为，如果随机抽样的话，我们无法控制输出的内容，若加入了条件，则可以限制生成的范围，因此，条件生成模型似乎更有其实用的价值，比如：用条件生成模型可输入条件1，生成1的图像。
为了实现这个条件生成模型，[2]在公式(2)中加入了条件，于是有：
$$\mathbf{y}=\tanh (W_{k,f}\ast \mathbf{x}+V_{k,f}^T\ast \mathbf{h})\odot \sigma (W_{k,g}\ast \mathbf{x}+V_{k,g}^T\ast \mathbf{h})(4)$$
(4)中，$k$ 是指第k层，$\mathbf{h}$ 表示条件，它可以是one-hot，也可以是其他的信息。条件模型的这个特性，正好可以应用在VQ-VAE2 中，以生成新的图片。

五、应用在VQ-VAE2 中的 PixelCNN

VQ-VAE2是近期Aaron van den Oord 的一篇文章[5]提出的生成模型，该团队向世人展示了一种媲美BigGan的基于最大似然思想的生成模型，生成的图片几可以假乱真，如图10：

图10 使用VQ-VAE2 生成的图片

VQ-VAE2 是VQ-VAE的升级版，而VQ-VAE是一种离散化的矢量量化VAE方案。我们先回顾一下 VAE 的工作原理：
VAE由三部分组成：编码器（Encoder），隐变量（Latent Variables），解码器（Decoder）。当编码器输入（$\mathbf{x}$ ），则输出隐变量（$\mathbf{v}$），编码器相当于 $p_{\theta }(\mathbf{v}|\mathbf{x})$；$\mathbf{v}$ 是一组正态分布的均值（ $\mu$）和方差（ $\sigma$）；而 $\mathbf{v}$ 本身满足一定的分布，一般取 $p(\mathbf{v})$ 也是正态分布；根据 $p(\mathbf{v})$ 对 $\mathbf{v}$ 抽样，得到 $\hat{\mathbf{v}}$；将 $\hat{\mathbf{v}}$ 作为解码器的输入，解码器完成重构任务，得到 $\hat{\mathbf{x}}$，解码器相当于 $p_{\phi }(\hat{\mathbf{x}}|\hat{\mathbf{v}})$；VAE的训练过程就是调整参数 $\theta ,\phi$ 使 $(\mathbf{x},\hat{\mathbf{x}})$ 的似然最大化的过程。

VQ-VAE 是VAE的一个矢量量化方案，它与普通VAE最大不同的地方是它的隐变量（$\hat{\mathbf{v}}$）不是连续的，而是离散的，是在一个矢量码表中选出来的。当编码器输出 $\mathbf{v}$ 后，用 $\mathbf{v}$ 去查矢量码表，得到离散的矢量量化编码 $\hat{\mathbf{v}}$，将 $\hat{\mathbf{v}}$ 作为解码器输入，重构 $\hat{\mathbf{x}}$。此方案中，我们并没有设定隐变量 $p(\mathbf{v})$ 的分布，$p(\mathbf{v})$ 可以由 PixelCNN 通过学习样本集得到：

• 将 $p(\mathbf{v})$ 条件概率因子化：$p(\mathbf{v})={\prod }_{i=1}^{N}p(v_i|v_{<i})$
• 由 PixelCNN 学习得到各条件概率： $p(v_i|v_{<i})$
• 在生成图像时，利用该条件分布 $p(v_i|v_{<i})$ 逐点生成隐变量的矢量量化编码$\hat{\mathbf{v}}$，则可由解码器重构 $\hat{\mathbf{x}}$。

整个过程的关键是 ：PixelCNN 可以拟合一个离散随机变量的分布，而VQ-VAE的隐变量是一个离散分布，它们刚好匹配。

VQ-VAE2是VQ-VAE的升级版，其结构如图：

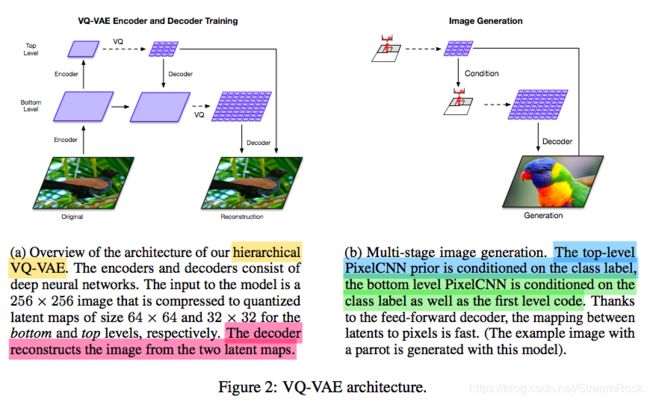
图11 VQ-VAE结构，(a)是Encoder, Decoder 训练时，采用的结构；(b)生成图像时采用的结构。

它将矢量量化分为了两级：top、bottom。Top级用于全局信息的量化（比如，形状），bottom级则是对局部信息的量化（比如：纹理）。VQ-VAE2的训练和生成分为两个阶段：第一阶段——训练Encoder和Decoder，如图11左图；第二阶段——生成图像，如图11右图。训练阶段按VQ-VAE的训练方法训练即可，在第二阶段生成图像时，则需要有另外的辅助网络——PixelCNN。先由top层的 PixelCNN 得到顶层的编码（${\hat{\mathbf{v}}}_t$）,再由该顶层编码作为bottom层 Conditional PixelCNN 的条件，生成底层编码（${\hat{\mathbf{v}}}_b$），然后，将（${\hat{\mathbf{v}}}_t$，${\hat{\mathbf{v}}}_b$）作为最终编码code，输入到解码器中重构 $\hat{\mathbf{x}}$。其完整的算法如下：

按VQ-VAE2方案，矢量量化还可以分成多层，进一步将矢量量化的抽象层次进行分离，图10就比较了1、2、3层VQ-VAE生成质量的差别。最后，我们来看看它的生成效果，已经十分接近真实图像，如下：

图12 VQ-VAE2 的生成图片效果

六、小结

最大似然类的生成模型（自回归型、VAEs）比隐概率模型类（GANs）在以下一些方面是有优点的：

• 似然类模型可以完全覆盖样本数据的各种模式，而GAN不行
• 似然类模型不会出现GAN的模式坍塌，笼统一些就是大概率能“训”出来，而GAN则不一定

似然类模型的不足在哪里呢？我觉得应该是其创造力不如GAN，它生成的东西中规中矩，质量也不弱于GAN，但多样性比不上GAN。我直觉的理解是，似然类的模型是没说对的，不做，而GAN则是没说错的，就做。若能有机地结合两者的能力，应该能创造出更好的生成模型，比如VQ-VAE就将两种似然类模型很好地结合在了一起。

---

[1] Pixel Recurrent Neural Networks, Aaron van den Oord, Nal Kalchbrenner, Koray Kavukcuoglu, Google DeepMind, 2016, https://arxiv.org/abs/1601.06759
[2] Conditional Image Generation with PixelCNN Decoders, Aaron van den Oord, Nal Kalchbrenner, Oriol Vinyals, Lasse Espeholt, Alex Graves, Koray Kavukcuoglu, Google DeepMind, 2016, https://arxiv.org/abs/1606.05328
[3] https://github.com/jzbontar/pixelcnn-pytorch/blob/master/main.py
[4] https://github.com/kkleidal/GatedPixelCNNPyTorch/blob/master/models/components/pixelcnn.py
[5] Generating Diverse High-Fidelity Images with VQ-VAE-2, Ali Razavi, Aaron van den Oord, Oriol Vinyals, Google DeepMind, 2019, https://arxiv.org/abs/1906.00446
[6] Andrew Brock, Jeff Donahue, and Karen Simonyan. Large scale GAN training for high fidelity natural image synthesis.