机器学习——神经网络
概念和组成
概念:我们在机器学习中谈论神经网络时,指的是神经网络学,或者说,是机器学习与神经网络这两个学科领域的交叉部分。我们在这里构建类似于神经模型的分类器,实则回到了分类的问题上。在训练过程中,神经网络的复杂性也体现了其分类的准确和可靠性很高的优点。
神经元模型
生物的知识用起来哦!你想一个最简单的神经要怎么兴奋,其过程大致分为,感受刺激 --> 钾离子外流,钠离子内流 --> 达到兴奋所需要的电位差立刻兴奋 --> 传导…
那么在机器学习中,我们的神经元长成啥样呢?肯定和我们自己的神经元有区别,至少不会流血。
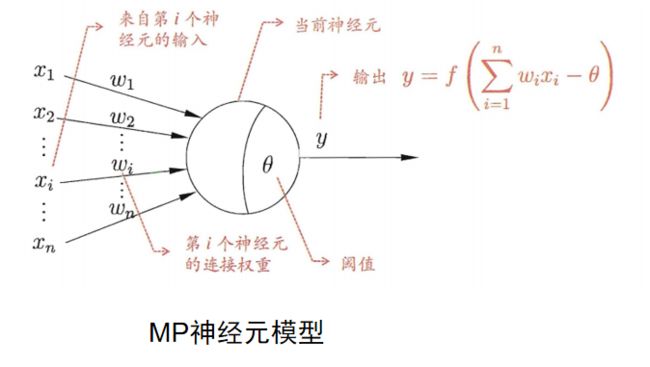 这个神经元 x 端是其他神经元传递过来的信号,w 表示权重。什么意思?就是你传过来的东西我要消化处理一下才传递给下一层级。比如吃饭时,把食物送进空腔,没牙的老奶奶也知道用牙床磨两下食物后再送进胃里。
这个神经元 x 端是其他神经元传递过来的信号,w 表示权重。什么意思?就是你传过来的东西我要消化处理一下才传递给下一层级。比如吃饭时,把食物送进空腔,没牙的老奶奶也知道用牙床磨两下食物后再送进胃里。

我们求学也要有自己的理解不是吗?这个 w 就是两个神经元“通道的带权值”。当前神经元里面有一个阈值,将这个神经元的总输入值和阈值比较,然后通过“激活函数”产生神经元的输出。
激活函数
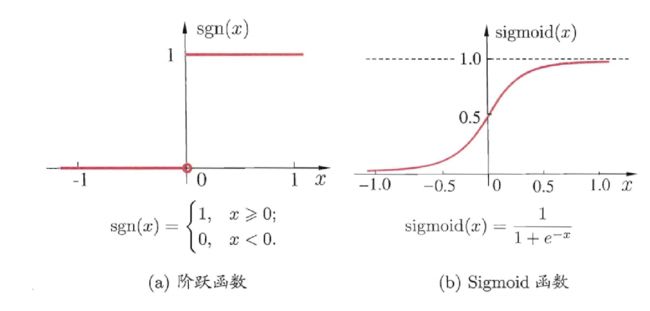
理想中的激活函数便是阶跃函数(左图),输出值只有0,1。0代表抑制,1代表兴奋,但是它不连续,不光滑,因此我们实际上用的是sigmoid函数(右图)作为激活函数。它把可能在较大范围内变化的输入值挤压到 (0 1) 输出值范围内,因此有 时也称为 “挤压函数”。
 事实上,从计算机科学的角度看,我们可以先不考虑神经网络是否真的模拟了生物神经网络,只需将一个神经网络视为包含了许多参数的数学模型,这个模型是若干个函数相互(嵌套)带入而得.有效的神经网络学习算法大多以数学证明为支撑的。知道小时候为啥需要学数学乐吧,你只要学深一点除了文科领域哪儿都逃不过数学。
事实上,从计算机科学的角度看,我们可以先不考虑神经网络是否真的模拟了生物神经网络,只需将一个神经网络视为包含了许多参数的数学模型,这个模型是若干个函数相互(嵌套)带入而得.有效的神经网络学习算法大多以数学证明为支撑的。知道小时候为啥需要学数学乐吧,你只要学深一点除了文科领域哪儿都逃不过数学。
感知机和神经网络
感知机由两层神经元组成,输入层接收外界输入信号后传递给输出层,输出层是M-P神经元,亦称"阔值逻辑单元".
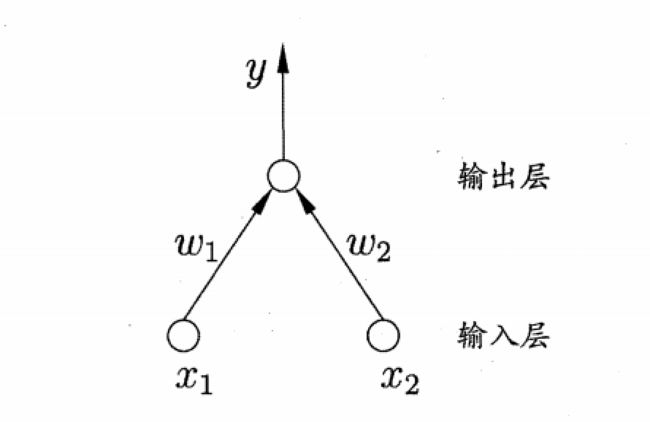 可是它太简单了,就跟膝跳反射似的不用动脑子。所以我们得增加它的层数实现更为精准理性的功能。在此之前我们还是得从这个简单的模型说起,万丈高楼平地起,好好看,好好学。
可是它太简单了,就跟膝跳反射似的不用动脑子。所以我们得增加它的层数实现更为精准理性的功能。在此之前我们还是得从这个简单的模型说起,万丈高楼平地起,好好看,好好学。
更一般的,在给定的训练集中,权重Wi(i=01,2…,n)和θ都是通过学习得到。域值θ可以看做固定输入的亚结点所对应的连接权重Wn+1。**这样权重和域值的学习可以统一为权重的学习。**感知机学习的规则,对于训练集(x,y),若对感知机的输出为y`,则感知机的权重将这样调整:
 其中η∈(0,1),称为学习效率,从第一个式子可以看出,当y`=y时,预测全部正确△Wi = 0,不调整,不相等就会根据二式调整。
其中η∈(0,1),称为学习效率,从第一个式子可以看出,当y`=y时,预测全部正确△Wi = 0,不调整,不相等就会根据二式调整。
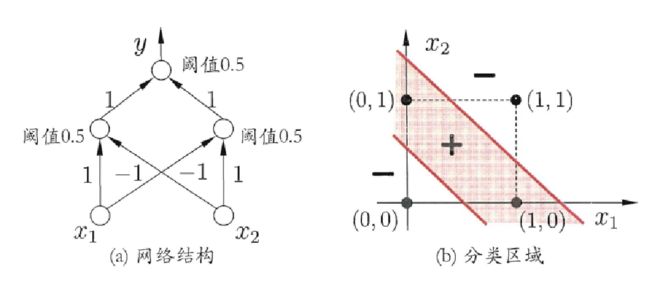
需要注意的是感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,其学习能力非常有限。与或非问题都是线性可分的,若两个模式线性可分则存在一个线性超平面把他们分开如图。则感知机学习过程一定会收敛求得权向量Wi.否则感知机学习过程将发生动荡不稳定,就不能解决d图的非线性可分问题。
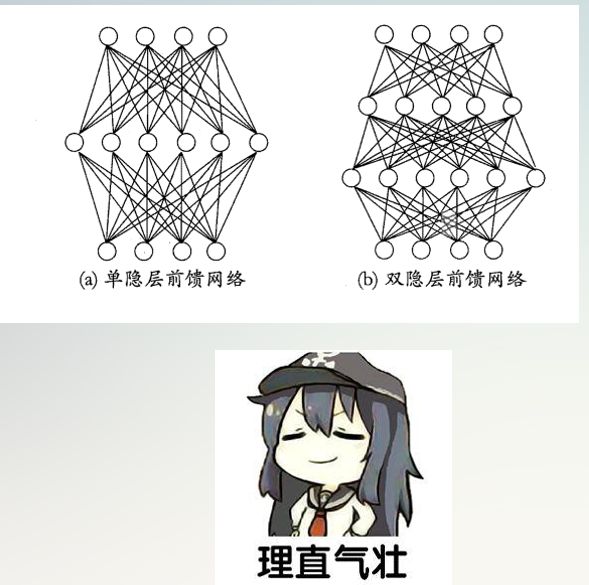
 要解决非线性可分问题,需要多层功能神经元。如下a图这个两层的感知机,输入层和输出层之间的一层,叫做隐层或隐含层。隐含层和输出层都具有激活函数的功能。
要解决非线性可分问题,需要多层功能神经元。如下a图这个两层的感知机,输入层和输出层之间的一层,叫做隐层或隐含层。隐含层和输出层都具有激活函数的功能。
 更一般地,常见的神经网络如下两图所示层级结构,每层神经元与下一层神经元全互联。神经元之间不存在同级连接也不存在跨级连接。这样的神经网络称为”多层前馈神经网络”。
更一般地,常见的神经网络如下两图所示层级结构,每层神经元与下一层神经元全互联。神经元之间不存在同级连接也不存在跨级连接。这样的神经网络称为”多层前馈神经网络”。
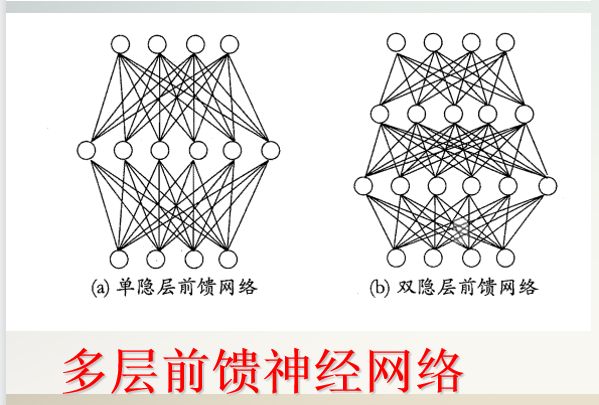 其中传入层神经元接收外界输入,隐层和输出层神经元对信号进行加工,最终结果有输出层神经元输出。强调输入层神经元只是接收输入,隐层和输出层包含功能神经元。图a叫做“两层网络”也叫作“单隐层网络”。在机器学习过程中,通过训练集来调整神经元之间的“连接权”以及每个功能神经元的域值。也就是说:神经元学的东西蕴含在连接权和域值里面。
其中传入层神经元接收外界输入,隐层和输出层神经元对信号进行加工,最终结果有输出层神经元输出。强调输入层神经元只是接收输入,隐层和输出层包含功能神经元。图a叫做“两层网络”也叫作“单隐层网络”。在机器学习过程中,通过训练集来调整神经元之间的“连接权”以及每个功能神经元的域值。也就是说:神经元学的东西蕴含在连接权和域值里面。
误差逆传播算法(标准BP)
介绍
多层网络的学习能力比单层感知机强得多,想要训练多层网络,简单的感知机学习规则显然不够。需要更强大的算法,误差逆传播算法(Error BackPropagation ,简称 BP)就是最杰出的算法代表。
功能
- 大多数现实中任务中使用的神经网络,都使用BP训练算法
- BP算法不仅可用于多层前馈神经网络,还可用于其他类型的神经网络。如:训练递归神经网络,一般我们指的BP网络都是训练的多层前馈网络。
公式推导
 给定训练集D={( x 1 x_1 x1, y 1 y_1 y1),( x 2 x_2 x2, y 2 y_2 y2)…( x m x_m xm, y m y_m ym)} x i x_i xi∈ R d R^d Rd, y i y_i yi∈ R l R^l Rl,输入事例由d个属性描述,输出l个实维向量。我们来看图:d个输入神经元,q个隐层神经元,l个输出神经元构成的多层前馈网络结构。第j个输出层神经元的域值用 θ j θ_j θj表示,隐层第h个神经元用γh表示。输入层第i个神经元和隐层第h个神经元之间的连接权记 v i h v_{ih} vih,隐层第h个神经元和输出层第j个神经元之间的连接权 ω h j ω_{hj} ωhj,记第h个神经元接收的输入为 α h α_h αh= ∑ d i = 1 v i h x i \sum_{d_i=1}v_{ih}x_i ∑di=1vihxi输出层第j个神经元接收的输入为 β j = ∑ q h = 1 ω h j b h β_j=∑_{q_h=1}ω_{hj}b_h βj=∑qh=1ωhjbh,其中bh为第h个隐层神经元的输出。
给定训练集D={( x 1 x_1 x1, y 1 y_1 y1),( x 2 x_2 x2, y 2 y_2 y2)…( x m x_m xm, y m y_m ym)} x i x_i xi∈ R d R^d Rd, y i y_i yi∈ R l R^l Rl,输入事例由d个属性描述,输出l个实维向量。我们来看图:d个输入神经元,q个隐层神经元,l个输出神经元构成的多层前馈网络结构。第j个输出层神经元的域值用 θ j θ_j θj表示,隐层第h个神经元用γh表示。输入层第i个神经元和隐层第h个神经元之间的连接权记 v i h v_{ih} vih,隐层第h个神经元和输出层第j个神经元之间的连接权 ω h j ω_{hj} ωhj,记第h个神经元接收的输入为 α h α_h αh= ∑ d i = 1 v i h x i \sum_{d_i=1}v_{ih}x_i ∑di=1vihxi输出层第j个神经元接收的输入为 β j = ∑ q h = 1 ω h j b h β_j=∑_{q_h=1}ω_{hj}b_h βj=∑qh=1ωhjbh,其中bh为第h个隐层神经元的输出。
假设隐层和输出层的神经元都使用sigmoid函数,对训练例 ( x k , y k ) (x_k,y_k) (xk,yk),假定神经网络的输出为 y ^ k = ( y 1 , y 2 . . . y ^ l k ) \hat y_k=(y_1,y_2...\hat y^{k}_l) y^k=(y1,y2...y^lk)
那么有: y ^ j k = f ( β j − θ j ) 1 \hat y^{k}_j=f(\beta_j-\theta_j)\qquad 1 y^jk=f(βj−θj)1
 根据算法名字我们知道从结果逆向更新权重值,我们用这个绿色的结点。注意强调: y j y_j yj是用sigmoid函数处理而来, β j , θ j \beta_j,\theta_j βj,θj分别表示 y j y_j yj的输入和域值。输入是所有隐层都参与了,累计求和而来。
根据算法名字我们知道从结果逆向更新权重值,我们用这个绿色的结点。注意强调: y j y_j yj是用sigmoid函数处理而来, β j , θ j \beta_j,\theta_j βj,θj分别表示 y j y_j yj的输入和域值。输入是所有隐层都参与了,累计求和而来。
输出的 y ^ \hat y y^和实际的 y y y有一个误差,我们就要借助它来更新权重和阈值,这里我们采用均方误差:
E k = 1 2 ∑ i = 1 l ( y ^ j − y j ) 2 2 E_k=\frac{1}{2}\sum_{i=1}^l(\hat y_j-y_j)^2\qquad2 Ek=21i=1∑l(y^j−yj)22
这里的 E k E_k Ek是输出层所有结点的误差处理,1/2是方便后面的求导。
我们更新估计式:
v = v + Δ v 3 v=v+\Delta v\qquad3 v=v+Δv3
Δ v = η ( y − y ^ ) x i 4 \Delta v=\eta(y-\hat y)x_i\qquad4 Δv=η(y−y^)xi4
现在我们来推导 w h j w_{hj} whj的链接权。BP算法基于梯度下降策略以目标的负梯度方向来调整,由输出层的误差E_k和给定的学习率 η \eta η:
Δ w h j = − η ∂ E k ∂ w h j 5 \Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}\qquad5 Δwhj=−η∂whj∂Ek5
注意 w h j w_{hj} whj先影响到第j个输出层神经元的输入值βj,再影响到输出 y ^ j k \hat y_{j}^k y^jk最后影响到 E k E_k Ek,那么就类似于我们的符合函数,进行链式求导。
∂ E k ∂ w h j = ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j ⋅ ∂ β j ∂ w h j 6 \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat y_{j}^k}\cdot\frac{\partial \hat y_{j}^k}{\partial \beta_{j}}\cdot\frac{\partial \beta_{j}}{\partial w_{hj}}\qquad6 ∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj6
我们有βj的定义: β j = ∑ h = 1 q w h j b h 7 \beta _j=\sum_{h=1}^qw_{hj}b_h\qquad7 βj=h=1∑qwhjbh7
有: ∂ β j ∂ w h j = b h \frac{\partial \beta_j}{\partial w_{hj}}=b_h ∂whj∂βj=bh
 sigmoid函数有一个非常好的导数性质:
sigmoid函数有一个非常好的导数性质:
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
由公式 1 和 2 我们设一个 g i g_i gi
g i = − ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j g_i=-\frac{\partial E_k}{\partial \hat y_{j}^k}\cdot\frac{\partial \hat y_{j}^k}{\partial \beta_{j}} gi=−∂y^jk∂Ek⋅∂βj∂y^jk
= − ( y ^ j k − y j k ) f ′ ( β j − θ j ) \qquad=-(\hat y_{j}^k-y_{j}^k)f'(\beta_j-\theta_j) =−(y^jk−yjk)f′(βj−θj)
= y ^ j k ( 1 − y ^ j k ) ( y j k − y ^ j k ) =\hat y_{j}^k(1-\hat y_{j}^k)(y_{j}^k-\hat y_{j}^k) =y^jk(1−y^jk)(yjk−y^jk)
 带入 5 公式:
带入 5 公式:
Δ w h j = η g j b h \Delta w_{hj}=\eta g_jb_h Δwhj=ηgjbh
类似可得: Δ θ j = − η g j \Delta \theta_j=-\eta g_j Δθj=−ηgj
我们求下一层的权重变化 ΔVih,如法炮制一遍:
Δ v i h = − η ∂ E k ∂ v i h \Delta v_{ih}=-\eta \frac{\partial E_k}{\partial v_{ih}} Δvih=−η∂vih∂Ek
链式求导找关系,在上述的关系上要新增 w h j w_{hj} whj-> b h b_h bh-> v i h v_{ih} vih :
∂ E k ∂ v i h = ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j ⋅ ∂ β j ∂ w h j ⋅ ∂ w h j ∂ b h ⋅ ∂ b h ∂ α h ⋅ ∂ α h ∂ v i h \frac{\partial E_k}{\partial v_{ih}}=\frac{\partial E_k}{\partial \hat y_{j}^k}\cdot\frac{\partial \hat y_{j}^k}{\partial \beta_{j}}\cdot\frac{\partial \beta_j}{\partial w_{hj}}\cdot\frac{\partial w_{hj}}{\partial b_h}\cdot\frac{\partial b_h}{\partial \alpha_h}\cdot\frac{\partial \alpha_{h}}{\partial v_{ih}} ∂vih∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj⋅∂bh∂whj⋅∂αh∂bh⋅∂vih∂αh
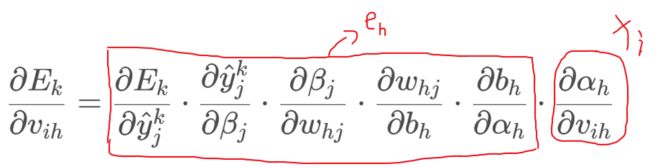
同时我们引入 e h e_h eh: e h = − ∂ E k ∂ b h ⋅ ∂ b h ∂ α h e_h=-\frac{\partial E_k}{\partial b_h}\cdot\frac{\partial b_h}{\partial \alpha_h} eh=−∂bh∂Ek⋅∂αh∂bh
= − ∑ j = 1 l ∂ E k ∂ β j ⋅ ∂ β j ∂ b h f ′ ( α h − γ h ) =-\sum_{j=1}^l\frac{\partial E_k}{\partial \beta_j}\cdot\frac{\partial \beta_j}{\partial b_h}f'(\alpha_h-\gamma _h) =−j=1∑l∂βj∂Ek⋅∂bh∂βjf′(αh−γh)
= ∑ j = 1 l g i w h j f ′ ( α h − γ h ) =\sum_{j=1}^lg_iw_{hj}f'(\alpha_h-\gamma_h) =j=1∑lgiwhjf′(αh−γh)
= b h ( 1 − b h ) ∑ j = 1 l g i w h j =b_h(1-b_h)\sum_{j=1}^lg_iw_{hj} =bh(1−bh)j=1∑lgiwhj
从而对隐层的更新:
Δ v i h = η e h x i \Delta v_{ih}=\eta e_hx_i Δvih=ηehxi
Δ γ h = − η e h \Delta\gamma _h=-\eta e_h Δγh=−ηeh
学习率η∈(0,1)控制着算法每一轮的迭代中更新步长,η太大容易振荡,太小收敛太慢了(就是 y ^ = y \hat y=y y^=y这个过程)。我们要做到精细可以是每一层的η都不一样,比如此处我们不妨设输出层η1,隐层η2。
工作流程
累计BP算法
我们需要注意BP算法的目标是要最小化训练集D上的累计误差:
E = 1 m ∑ k = 1 m E k E=\frac{1}{m}\sum_{k=1}^mE_k E=m1k=1∑mEk
我们上面说的是标准BP算法,每一次仅对一个训练样例更新连接权和阈值,其更新规则是根据单个的Ek而言。如果类似的推导基于累积误差最小化的更新规则,就得到了累积误差逆传播算法。这两个算法都很常用,标准BP算法往往需要进行更多次的迭代,而累积BP算法读取整个训练集D一遍后才对参数进行更新,其更新频率低很多。但是在很多任务中,累计误差Ek下降到一定程度后,进一步下降会非常缓慢,这是标准BP往往会更快获得较好的解。数据多更新次数越多标准BP较好
新问题拟合
现在任然未解决的问题:隐层的神经元到底需要几个?我们无法通过数据样例准确给出,只能通过试错法来确定隐层神经元的个数。
拟合问题
正是由于神经网络强大的表示能力,BP神经网络经常曹禺拟合:其训练误差逐渐降低,但是测试误差可能持续升高。
解决之道
1.早停:将数据分成训练集和验证集,训练集用来计算梯度、更新连接权和阈值,验证集用来估计误差。如果训练集误差降低,验证集的误差反而升高,立刻终止训练,同时返回最小误差的连接权和阈值。
2.正则化:在误差目标中增加一个用于描述网络复杂的部分,例如连接权和阈值的平方和. E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 E=\lambda \frac{1}{m}\sum_{k=1}^mE_k+(1-\lambda)\sum_{i}w_i^2 E=λm1k=1∑mEk+(1−λ)i∑wi2
其中λ∈(0,1)用于验证经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计。增加连接权与阈值平方和这一项后,训练过程将会偏向比较好的链接权和阈值,使网络输出更加平滑,从而对拟合有所缓解。
全局最小和局部最小
知识理解
我们神经网络的训练过程可以看做一个参数的寻优过程,即在参数空间中,寻找一组最优的链接权w,阈值参数θ使得误差E最小。
高数中我们知道参数最优在两个位置:局部极小、全局最小。直观来看,局部极小值是参数空间中的某个点,其邻域点的误差值均不小于该点的函数值;全局最小解便是参数空间中所欲点的误差值均不小于该点的误差函数值。
显然参数空间梯度为零的点,其误差函数就是局部极小值。想一想这个图,可能有多个极小值,最小值就藏在其中,我们就要把它找出来。
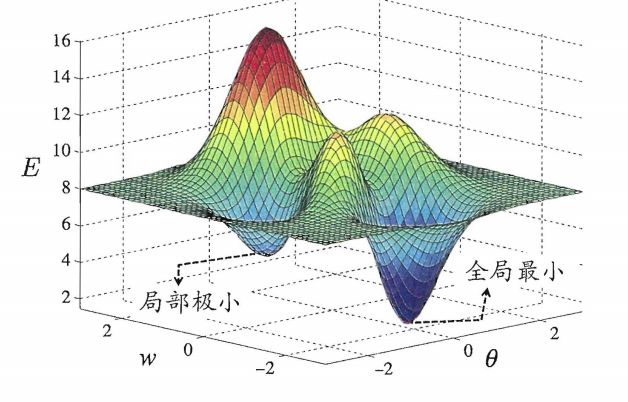
基于梯度的搜索是使用最广泛的参数寻优方法。我们每次进行迭代,计算误差函数在当前点的梯度,然后根据梯度确定搜索方向。这里我们负梯度方向为函数下降最快的方向,因此我们沿着这个方向寻找最优解,当梯度为零就是达到了局部极小值,既可以停止搜索了。可是多个极值点的情况我们只能找到一个极值点就停止了,就好比说我要去找西瓜,你看见路边的芝麻就停止了寻找,显然不能这样。
跳出局部极小
我们通常采用以下策略:
- 用多组不同的参数初始化神经网络,按标椎方法训练后,取其中误差最小的解作为最终参数。这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小,从其中选择最接近全局最小的哪个参数组作为结果。
- 使用“模拟退火”技术,每一步都有一定的概率接受比当前解更差的结果,从而有助于。在每次迭代中选择次优解要随着时间的推移而逐渐降低,从而保证算法的稳定。
- 使用随机梯度下降,与标准梯度下降精确计算梯度不同,随机梯度下降在算法中添加了随机因素。那么即使陷入了局部极小,但是梯度不为零啊,继续更新,这样有机会跳出局部最小继续搜索。
这些解决之道都是启发式,在理论上还缺乏保证。也就是你可以靠一定的概率接近或者取到全局最小,但是也有风险取不到。
BP算法举例
多说无益,我们来看最直观的数据运行过程,放松一下头脑,马上发车。
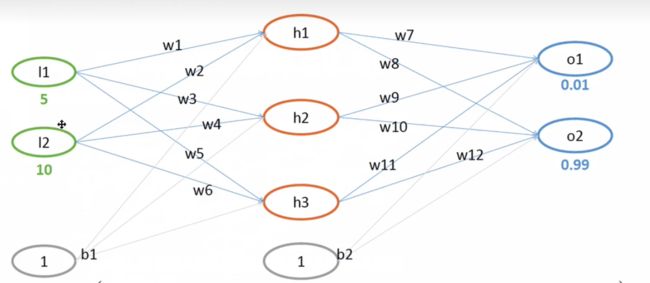 这里我们输出层 2 个神经元,隐层 3 个神经元,输出层 2 个神经元。
这里我们输出层 2 个神经元,隐层 3 个神经元,输出层 2 个神经元。
初始权重值:
| 连接权 | w1 | w2 | w3 | w4 | w5 | w6 | w7 | w8 | w9 | w10 | w11 | w12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 权值 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 |
偏执项b1=0.35 b2=0.65
我们先进行前向传播。(我都用手写了,你们也试一下吧,抄一遍也可以)
**接下来算输出层的输入值和输出值。**如法炮制一遍。
我们得到了第一轮的均方误差E,现在我们以更新 w7 权重为例来更新权值。
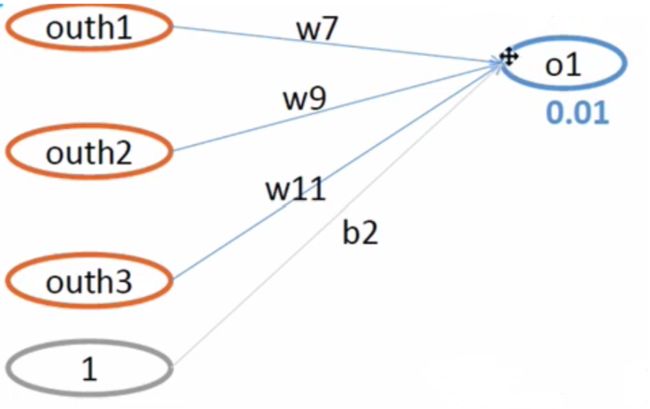
我们根据公式:
Δ w 7 = − η ∂ E t o t a l ∂ w 7 \Delta w_{7}=-\eta\frac{\partial E_{total}}{\partial w_7} Δw7=−η∂w7∂Etotal
请我们已经求出了 ∂ E t o t a l ∂ w 7 \frac{\partial E_{total}}{\partial w_7} ∂w7∂Etotal,加入我们初始化η=0.5
那么根据 w7 的更新公式:
w 7 + = w 7 + Δ w 7 w_7^+=w7+\Delta w_7 w7+=w7+Δw7
w 7 + = 0.4 − 0.5 ∗ 0.078064 = 0.360968 w_7^+=0.4-0.5*0.078064=0.360968 w7+=0.4−0.5∗0.078064=0.360968
同理我们可以求出:
w 8 + = 0.453383 w_8^+=0.453383 w8+=0.453383 w 9 + = 0.458137 \qquad w_9^+=0.458137 w9+=0.458137
w 10 + = 0.553629 w_{10}^+=0.553629 w10+=0.553629 w 11 + = 0.557448 \qquad w_{11}^+=0.557448 w11+=0.557448
w 12 + = 0.653688 w_{12}^+=0.653688 w12+=0.653688
结合初始值这张表:w7~w12
| 连接权 | w1 | w2 | w3 | w4 | w5 | w6 | w7 | w8 | w9 | w10 | w11 | w12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 权值 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 |
| 我们发现 w 7 w_{7} w7的值0.4更新为 w 7 + w_{7}^+ w7+ = 0.360968 它变小了, w 9 + w_{9}^+ w9+, w 11 + w_{11}^+ w11+也变小了.另外 w 8 + w_{8}^+ w8+ , w 10 + w_{10}^+ w10+ , w 12 + w_{12}^+ w12+变大了。 |
接下来我们来进行 w 1 w_1 w1的更新,看看关系图找出求导的关系链
 用笔推一下,流程大致这样:
用笔推一下,流程大致这样:

特别注意:这里的 w 7 w_7 w7 已经更新过了
类似的:
∂ E o 2 ∂ b h 1 = ∂ E o 2 ∂ y ^ 2 ⋅ ∂ y ^ 2 ∂ β 2 ⋅ ∂ β 2 ∂ b h 1 = ( y ^ 2 − y 2 ) y ^ 2 ( 1 − y ^ 2 ) w 8 \frac{\partial \,E_{o2}}{\partial\, b_{h1}}=\frac{\partial \,E_{o2}}{\partial\, \hat y_{2}}\cdot\frac{\partial \,\hat y_{2}}{\partial\, \beta _{2}}\cdot\frac{\partial \,\beta_{2}}{\partial\, b_{h1}}=(\hat y_2-y_2)\hat y_2(1-\hat y_2)w_8 ∂bh1∂Eo2=∂y^2∂Eo2⋅∂β2∂y^2⋅∂bh1∂β2=(y^2−y2)y^2(1−y^2)w8
计算出 ∂ E o 2 ∂ b h 1 \frac{\partial \,E_{o2}}{\partial\, b_{h1}} ∂bh1∂Eo2=-0.453383,然后计算出 ∂ E t o t a l ∂ w 1 = 0.011204 \frac{\partial \,E_{total}}{\partial\, w_{1}}=0.011204 ∂w1∂Etotal=0.011204.进而: w 1 + = w 1 + Δ w 1 = 0.1 − η ∂ E t o t a l ∂ w 1 = 0.1 − 0.5 ∗ 0.011204 = 0.094534 w_1^+=w1+\Delta w_1=0.1-\eta \frac{\partial \,E_{total}}{\partial\, w_{1}}=0.1-0.5*0.011204=0.094534 w1+=w1+Δw1=0.1−η∂w1∂Etotal=0.1−0.5∗0.011204=0.094534
类似的更新出其他连接权值:
 越往前面更新权值,它的计算复杂度会更高,消耗也更大。更新次数越多,就越接近真实值。
越往前面更新权值,它的计算复杂度会更高,消耗也更大。更新次数越多,就越接近真实值。

代码实现
这里我采用我老师的代码,里面附加详解。我老师的代码