Java KMP(Knuth-Morris-Pratt )搜索算法代码实现详解

本期目录

一，Knuth Morris Pratt搜索算法介绍

二，Knuth Morris Pratt搜索算法思路

三，Knuth Morris Pratt搜索算法代码实现

四，Knuth Morris Pratt搜索算法总结

五，Knuth Morris Pratt 完整代码

---

一，Knuth Morris Pratt搜索算法介绍

KMP是一种用于在给定文本中查找算法(其实就是改进的字符串匹配算法)。该算法由Donald Knuth，Vaughan Pratt和James Morris开发，KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

二，Knuth Morris Pratt搜索算法思路

在此搜索中，首先编译 给定的模式。通过编译它，我们尝试找到模式字符串的前缀和后缀。当不匹配发生时，这对我们有帮助-我们将不会从索引的开头开始寻找下一个匹配项。

取而代之的是，我们跳过文本字符串中已经比较过的部分，并开始进行超出该部分的比较。我们通过了解前缀和后缀来确定此部分，因此我们确定已经比较了哪个部分并且可以安全地跳过该部分。

跳过的结果是，我们可以节省很多比较，并且KMP的执行速度比纯朴的蛮力算法要快。

找了一张KMP匹配过程图片，红色是采用KMP算法的执行过程。

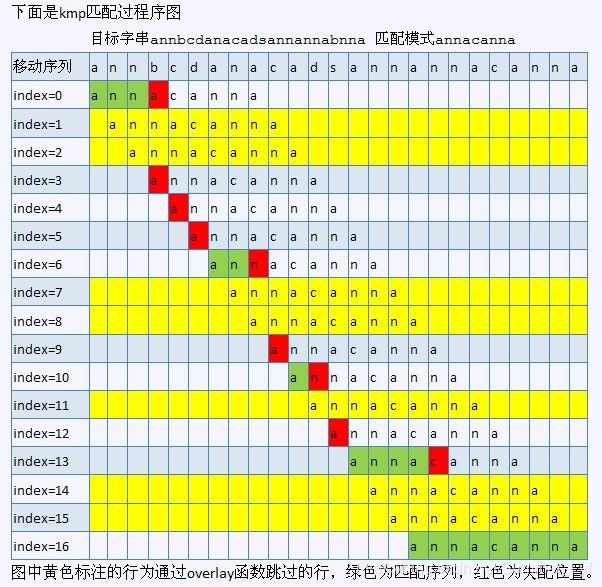（图片来源：https://mobile.51cto.com/news-455986.htm）

三，Knuth Morris Pratt搜索算法代码实现

首先创建编译模式数组，稍后将由KMP搜索算法使用该方法：

  /**
   * 创建模式数组，稍后将由KMP搜索算法使用该方法
   * @param pattern
   * @return
   */
  public static int[] compilePatternArray(String pattern) {
    int patternLength = pattern.length();
    int len = 0;
    int i = 1;
    int[] compliedPatternArray = new int[patternLength];
    compliedPatternArray[0] = 0;

    while (i < patternLength) {
      if (pattern.charAt(i) == pattern.charAt(len)) {
        len++;
        compliedPatternArray[i] = len;
        i++;
      } else {
        if (len != 0) {
          len = compliedPatternArray[len - 1];
        } else {
          compliedPatternArray[i] = len;
          i++;
        }
      }
    }
    System.out.println("模式数组" + Arrays.toString(compliedPatternArray));
    return compliedPatternArray;
  }

可以将已编译的模式数组视为存储模式数组中字符模式的数组。创建此数组的主要目的是在模式中找到前缀和后缀。如果我们知道模式中的这些元素，则可以避免从文本开头进行比较，而仅在发生不匹配之后比较下一个字符。

编译后的数组在模式数组中存储当前字符的先前出现的索引位置。

让我们实现算法本身：

 /**
   * KMP算法
   * @param text
   * @param pattern
   * @return
   */
  public static List performKMPSearch(String text, String pattern) {
    //调用compilePatternArray()方法
    int[] compliedPatternArray = compilePatternArray(pattern);

    int textIndex = 0;
    int patternIndex = 0;

    List foundIndexes = new ArrayList<>();

    while (textIndex < text.length()) {
      if (pattern.charAt(patternIndex) == text.charAt(textIndex)) {
        patternIndex++;
        textIndex++;
      }
      if (patternIndex == pattern.length()) {
        foundIndexes.add(textIndex - patternIndex);
        patternIndex = compliedPatternArray[patternIndex - 1];
      }

      else if (textIndex < text.length() && pattern.charAt(patternIndex) != text.charAt(textIndex)) {
        if (patternIndex != 0)
          patternIndex = compliedPatternArray[patternIndex - 1];
        else
          textIndex = textIndex + 1;
      }
    }
    return foundIndexes;
  }

在这里，我们先依次比较模式和文本数组中的字符。我们一直在前进，直到获得模式和文本数组的匹配为止。这样，如果我们在匹配时到达模式数组的末尾，则意味着我们在文本中发现了一个模式。

但是，如果在比较两个数组时发现不匹配，则将模式字符数组索引移至中的值，compiledPatternArray()并移至文本数组中的下一个字符。这是KMP搜索击败暴力手段的地方，因为如果出现不匹配，它不会多次比较文本字符。

让我们尝试运行算法：

 public static void main(String[] args) {
    String pattern = "AAABAAA";
    String text = "ASBNSAAAAAABAAAAABAAAAAGAHUHDJKDDKSHAAJF";

    List foundIndexes = SearchAlgorithms.performKMPSearch(text, pattern);

    if (foundIndexes.isEmpty()) {
      System.out.println("在给定文本字符串中没有找到");
    } else {
      System.out.println("在给定文本字符串中找到: " +foundIndexes.stream().map(Object::toString).collect(
          Collectors.joining(", ")));
    }
  }

在模式文本中AAABAAA，观察到以下模式并将其编码在模式数组中：

• 模式A（单个A）在索引1中重复，并在4处重复。
• 模式AA（两个 A）在索引2中重复，并在索引5中重复。
• 模式AAA（3 A）在索引6处重复。

输出结果：

我们描述的模式在输出的已编译模式数组中清楚地显示给我们。

借助此编译数组，KMP搜索算法可以在文本中搜索给定模式，而无需移回文本数组。

四，Knuth Morris Pratt搜索算法总结

时间复杂度

该算法需要比较给定文本中的所有元素以找到模式。所需时间为O（N）。为了编译模式字符串，我们需要访问模式中的每个字符，这是另一个O（M）迭代。

因此，此算法花费的总时间为O（M + N）。

空间复杂度

我们需要O（M）空间来存储给定大小的模式的已编译模式M。

该算法特别用于文本工具中以在文本文件中查找模式。

五，Knuth Morris Pratt 完整代码

If you are interested, try it.

public class SearchAlgorithms {

  /**
   * 创建模式数组，稍后将由KMP搜索算法使用该方法
   * @param pattern
   * @return
   */
  public static int[] compilePatternArray(String pattern) {
    int patternLength = pattern.length();
    int len = 0;
    int i = 1;
    int[] compliedPatternArray = new int[patternLength];
    compliedPatternArray[0] = 0;

    while (i < patternLength) {
      if (pattern.charAt(i) == pattern.charAt(len)) {
        len++;
        compliedPatternArray[i] = len;
        i++;
      } else {
        if (len != 0) {
          len = compliedPatternArray[len - 1];
        } else {
          compliedPatternArray[i] = len;
          i++;
        }
      }
    }
    System.out.println("模式数组" + Arrays.toString(compliedPatternArray));
    return compliedPatternArray;
  }

  /**
   * KMP算法
   * @param text
   * @param pattern
   * @return
   */
  public static List performKMPSearch(String text, String pattern) {
    //调用compilePatternArray()方法
    int[] compliedPatternArray = compilePatternArray(pattern);

    int textIndex = 0;
    int patternIndex = 0;

    List foundIndexes = new ArrayList<>();

    while (textIndex < text.length()) {
      if (pattern.charAt(patternIndex) == text.charAt(textIndex)) {
        patternIndex++;
        textIndex++;
      }
      if (patternIndex == pattern.length()) {
        foundIndexes.add(textIndex - patternIndex);
        patternIndex = compliedPatternArray[patternIndex - 1];
      }

      else if (textIndex < text.length() && pattern.charAt(patternIndex) != text.charAt(textIndex)) {
        if (patternIndex != 0)
          patternIndex = compliedPatternArray[patternIndex - 1];
        else
          textIndex = textIndex + 1;
      }
    }
    return foundIndexes;
  }
  //测试一下
  public static void main(String[] args) {
    String pattern = "AAABAAA";
    String text = "ASBNSAAAAAABAAAAABAAAAAGAHUHDJKDDKSHAAJF";

    List foundIndexes = SearchAlgorithms.performKMPSearch(text, pattern);

    if (foundIndexes.isEmpty()) {
      System.out.println("在给定文本字符串中没有找到");
    } else {
      System.out.println("在给定文本字符串中找到: " +foundIndexes.stream().map(Object::toString).collect(
          Collectors.joining(", ")));
    }
  }
}