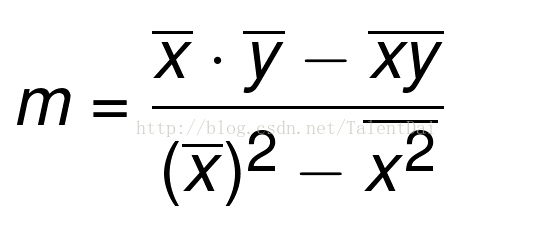机器学习教程 三.回归理论及代码实现

“有些事情我们知道我们知道这些事，我们还知道有些事情我们知道我们不知道。这就是说，有些事情我们不知道，但是还有些我们不知道我们不知道，也就是说有些事情我们不知道我们不知道这些事。”——《已知与未知》（Known and Unknown）。

对于“有些事情我们不知道我们不知道这些事”正需要我们通过探索学习才能发现“新大陆”，那么今天我们把这任务交给机器学习吧！嘿嘿。。接下来开始我们的学习这篇博客中我们将要学到：

1，如何计算线性回归方程的斜率和截距

2，用python语言实现线性回归算法

3，如何判断模型拟合的好坏

第二篇教程我们已经知道如何用sklearn中的回归来预测股票了，这篇教程我会深入的讨论回归算法，虽然我们没有必要深入了解所有的数学,线性代数在机器学习中是至关重要的,我们以后都会经常用到它。有兴趣可以自己多了解这方面知识。我们知道线性代数可以计算空间向量点之间的关系。同样，我们也可以把它应用于数据集的特征。还记得记得在我们定义线性回归研究的数据类型为连续性数据吗?使用简单的线性回归可以寻找数据集的最佳拟合线。如果数据不是连续的，那么就不会有最佳的拟合线？让我们看看一些例子:

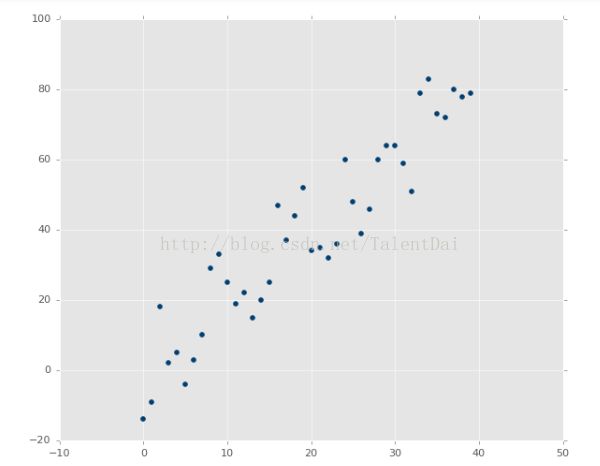
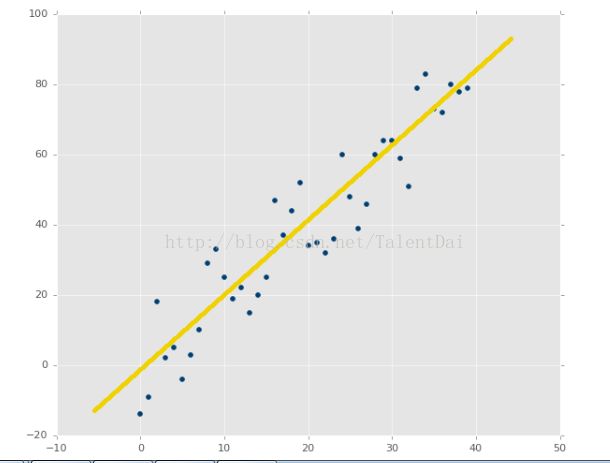
上面的图像显然具有很好的相关性。如果你被要求根据估计来画一条最合适的线，我们可以很容易地拟合出最佳的函数:

从上图X和y之间有一种关系(相关性)，我们可以看出根据一个Y可以预测一个X，或者说根据一个X预测一个Y，我们完成预测图中的点，需要一个线性代数的支持。 现在，我们回顾一下初中的知识，简单直线的定义:y = mx + b，其中m是斜率，b是轴截距。我们只要知道合适m（斜率）和b（截距）我们就能计算出x对应的Y了。
最佳拟合线的斜率m定义为:

知道了m，我也可以求b：

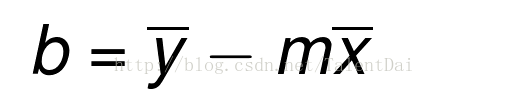
这一部分都是基础知识，可能到现在我们有这样的想法，学这线性回归和高大上的机器学习有什么关系?其实我们可以把线性回归比作机器学习建筑的一块砖。它几乎适用于每一个主要的机器学习算法，因此对它的理解将帮助您更快速了解其他机器学习算法，对我们来说，理解线性回归和一般的线性代数是我们编写自定义机器学习算法的第一步，并可以将它扩展到机器学习的前沿领域。随着技术的改进和硬件体系结构的改变，用于机器学习的方法也会发生变化。最近神经网络的兴起与一般的图形处理有很大的关系。你知道人工神经网络的核心是什么?你猜对了:线性回归。是不是很激动，哈哈，下面我们开始着手写代码，首先我们是先导入必要的库：

from statistics import mean
import numpy as np

我们从statistics导入mean，我们将很容易得到一个列表或数组的平均值，导入numpy我是为了很好处理矩阵，列表。现在我们来建立一个函数来计算m，这是我们的回归线的斜率:

def best_fit_slope(xs,ys):
    m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
         ((mean(xs)**2) - mean(xs*xs)))
    return m

下面我们来定义一些数据：

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

 ok，我们可以计算m了：
m = best_fit_slope(xs,ys)
print(m)

结果为：

我们接着来写一个函数计算b，非常简单：

def best_fit_intercept(xs,ys):
    b = mean(ys) - m*mean(xs)
    return b
同样我们也可以计算b了
b=best_fit_intercept(xs,ys)
print(b)

结果为：

当然我们希望程序简单明了，我将这两个函数合并：

def best_fit_slope_and_intercept(xs,ys):
    m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
         ((mean(xs)*mean(xs)) - mean(xs*xs)))
    b = mean(ys) - m*mean(xs)
    return m, b

m, b = best_fit_slope_and_intercept(xs,ys)
print(m,b)

结果为：

 

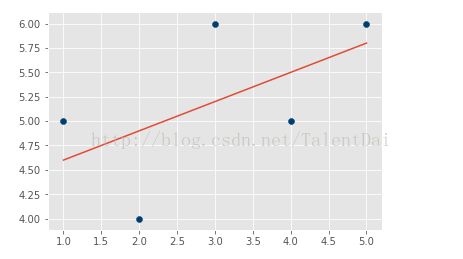
完美！斜率和截距都有了，我们终于可以拟合这条最佳线了，接下来我开始做传说中的可视化了，哈哈哈。。
首先我们先创建我们拟合的数据

regression_line=[]
for x in xs:
    regression_line.append((m*x)+b)

现在我么要导入我们需要库：

import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')

# 作图：
# 绘制现有数据的散点图
plt.scatter(xs,ys,color='#003F72')
# 绘制回归线
plt.plot(xs, regression_line)
# 最后显示它
plt.show()

结果为：

是不是很有成就感，也许你对matplotlib，numpy，pandas等库不了解，还是那句话不要急，跟着敲一遍，有空可以查查资料，要学东西太多， 我们要做的是把自己学过东西掌握，不经意我又来了一碗鸡汤。。。现在我们已经知道如何创建我们自己的模型，非常棒，可是我们的模型是否精确呢?
我们知道检查错误的标准方法可以使用使用平方误差。接下来你会听到这个方法叫r2或确定系数。。。首先我们来理解一些基本的概念：

假设一数据集包括  共n个观察值，相对应的模型预测值分别为  

# 总体平方和TSS( total sum of squares)：

# 回归平方和RSS(regression sum of squares)：

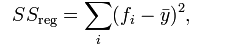
# 残差平方和ESS(Residual sum of squares)：

# 其中，yi表示实验数据，fi 表示模拟值，表示样本平均值。
# 决定系数(Coefficient of determination)：

# 在一定程度上反应了模型的拟合优度。
# 其实就是回归平方和在总体平方和中所占的比例。因为TSS＝RSS+ESS

没错，我们可以这么看R2：

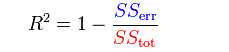
PS：为什么我们不直接把误差加起来还要平方呢？我们想要把误差归为一段距离，但是误差可能是- 5，但是经过平方后变成一个这是一个正数。其实这里我们可以用绝对值，有些极端的离群值存在时，但是我们不关心它们， 我们可以考虑把平方换成绝对值。如果我们很关心离群值，我们需要更高的指数。这里我们用平方，因为这是大家习惯使用的标准。

这里我们已经知道了决定系数，下面我开始编程了，首先我们定义一个平方误差函数：

def squared_error(ys_orig,ys_line):
    return sum((ys_line - ys_orig) * (ys_line - ys_orig))

 接下来，我们定义R2函数：

def coefficient_of_determination(ys_orig,ys_line):
    y_mean_line = [mean(ys_orig) for y in ys_orig]
    squared_error_regr = squared_error(ys_orig, ys_line)
    squared_error_y_mean = squared_error(ys_orig, y_mean_line)
    return 1 - (squared_error_regr/squared_error_y_mean)

万事俱备只欠东风，我们开始测试我们之前的回归函数的精确度了，我就直接copy前面的代码：

from statistics import mean
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

def best_fit_slope_and_intercept(xs,ys):
    m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
         ((mean(xs)*mean(xs)) - mean(xs*xs)))
    b = mean(ys) - m*mean(xs)
    return m, b

def squared_error(ys_orig,ys_line):
    return sum((ys_line - ys_orig) * (ys_line - ys_orig))

def coefficient_of_determination(ys_orig,ys_line):
    y_mean_line = [mean(ys_orig) for y in ys_orig]
    squared_error_regr = squared_error(ys_orig, ys_line)
    squared_error_y_mean = squared_error(ys_orig, y_mean_line)
    return 1 - (squared_error_regr/squared_error_y_mean)
    
m, b = best_fit_slope_and_intercept(xs,ys)
regression_line = [(m*x)+b for x in xs]

r_squared = coefficient_of_determination(ys,regression_line)
print(r_squared)

结果为：

 

晕，，，搞了那么久，这么很低的值，显然我们的最佳拟合线并不是很好.稍安勿躁，我们来看看我们的数据集，这是我们随便打的数据， 在某些点上，从值到值的方差是20 - 50%，这是非常高的方差，还有一点就是数据量有点小了。。。不知不觉我们已经学完了如何写回归方程，如何通过判定系数来估测我们回归方程的精确程度。。。是不是很有收获？如果还是迷茫，别怕，路漫漫其修远兮，吾将上下而求索。慢慢来跟着我的脚步接着学，也许在将来某个阶段你会想通的。。哈哈哈，下一篇我们即将学习K近邻算法（KNN）。