红黑树-JAVA实现(红黑树插入和删除)
红黑树介绍
红黑树是平衡二叉查找树的一种。平衡树在插入和删除的时候,会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。AVL树由于实现比较复杂,而且插入和删除性能差,在实际环境下的应用不如红黑树。红黑树(Red-Black Tree,以下简称RBTree)的实际应用非常广泛,比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等,各种语言的函数库如Java的TreeMap和TreeSet,C++ STL的map、multimap、multiset等。RBTree也是函数式语言中最常用的持久数据结构之一,在计算几何中也有重要作用。值得一提的是,Java 8中HashMap的实现也因为用RBTree取代链表,性能有所提升。
RBTree的定义
-
任何一个节点都有颜色,黑色或者红色
-
根节点是黑色的
-
父子节点之间不能出现两个连续的红节点
-
任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等
-
空节点被认为是黑色的
public class RBTree> implements MyTree {
private Node root;
private Node nullNode;
private static final boolean BLACK=true;
private static final boolean RED =false;
private static class Node{
Node(AnyType d){
this.data =d;
this.left =null;
this.right =null;
this.parent =null;
this.color =RBTree.BLACK;
}
Node(AnyType d, Node left, Node right,Node parent,boolean color){
this.data =d;
this.left =left;
this.right =right;
this.parent =parent;
this.color =color;
}
AnyType data;
Node left;
Node right;
Node parent;
boolean color;
}
public RBTree(){
nullNode=new Node<>(null);
nullNode.parent=nullNode.left=nullNode.right=nullNode;
root=nullNode;
header=new Node<>(null, null, root, null, RBTree.BLACK);//header.right->root, null <- root.parent
}
@Override
public void makeEmpty() {
root=nullNode;
header.right=root;
}
@Override
public boolean isEmpty() {
return (root==nullNode);
}
@Override
public boolean contains(AnyType x) {
return (contains(x,root)!=nullNode);
}
@Override
public AnyType findMin() {
return isEmpty()?null:findMin(root).data;
}
@Override
public AnyType findMax() {
return isEmpty()?null:findMax(root).data;
}
@Override
public void insert(AnyType x) {
//root=topDownInsert(x);
Node node=new Node<>(x,nullNode,nullNode,nullNode,RED);
root=insert(node,root);
insertFixUp(node);
return;
}
@Override
public void remove(AnyType x) {
Node node=contains(x,root);
if(node!=nullNode)
remove(node);
}
@Override
public void printTree() {
if(isEmpty()){
System.out.println("It is empty.");
return;
}
printTree_m(root);
} /**省略代码**/}
红黑树主要操作
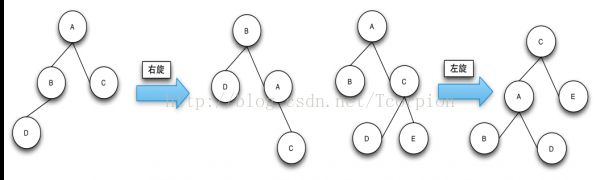
包括查找(最大、最小)、插入、删除,其中插入6种情况,删除8种情况。内部操作主要是:左旋转(leftRotate)、右旋转(rightRotate),每本书中的教程对左旋和右旋的方向定义有些出入,我自己这里的定义是:将一个子树的 “左儿子” 旋转到 “子树根” 位置称为左旋, 将一个子树的 “右儿子” 旋转到 “子树根” 位置称为右旋。
红黑树节点定义:
private static class Node{
Node(AnyType d){
this.data =d;
this.left =null;
this.right =null;
this.parent =null;
this.color =RBTree.BLACK;
}
Node(AnyType d, Node left, Node right,Node parent,boolean color){
this.data =d;
this.left =left;
this.right =right;
this.parent =parent;
this.color =color;
}
AnyType data;
Node left;
Node right;
Node parent;
boolean color;
} 红黑树内部旋转:
/**
* ----------------leftRotate-----------------------
* |k2| |k1|
* |k1| |Z| ---> |X| |k2|
* |X| |Y| |W| |Y| |Z|
* |W|
* ---------------------------------------------------
* |k2| |k1|
* |k1| |Z| ---> |X| |k2|
* |X| |Y| |Y| |Z|
* ---------------------------------------------------
* Errors would be arroused if k1 or k2 is null.
* */
private Node leftRotate(Node k2){
Node k1=k2.left;
if(nullNode==k2.parent){
root=k1;
header.right=k1;
}else{
if(k2==k2.parent.left){
k2.parent.left=k1;
}else{
k2.parent.right=k1;
}
}
k1.parent=k2.parent;
k2.left=k1.right;
if(null!=k1.right){
k1.right.parent=k2;
}
k1.right=k2;
k2.parent=k1;
return k1;
}
/**
* ----------------rightRotate----------------------
* |k1| |k2|
* |Z| |k2| ---> |k1| |Y|
* |X| |Y| |Z| |x| |W|
* |W|
* ---------------------------------------------------
* |k1| |k2|
* |Z| |k2| ---> |k1| |Y|
* |X| |Y| |Z| |x|
* ---------------------------------------------------
* Errors would be arroused if k1 or k2 is null.
* */
private Node rightRotate(Node k1){
Node k2=k1.right;
if(nullNode==k1.parent){
root=k2;
header.right=k2;
}else{
if(k1==k1.parent.left){
k1.parent.left=k2;
}else{
k1.parent.right=k2;
}
}
k2.parent=k1.parent;
k1.right=k2.left;
if(nullNode!=k2.left){
k2.left.parent=k1;
}
k2.left=k1;
k1.parent=k2;
return k2;
}
红黑树的搜索(最值、普通值):
/**
* Ensure r is not null.
* */
private Node findMax(Node r){
if(r.right==nullNode){
return r;
}
return findMax(r.right);
}
/**
* Ensure r is not null.
* */
private Node findMin(Node r){
if(r.left==nullNode){
return r;
}
return findMin(r.left);
}
/**
* @param x the searched value
* @param r the subtree being searched
* @return the result Node
* /
private Node contains(AnyType x,Node r){
if(r==nullNode){
return r;
}
if(x.compareTo(r.data)==0){
return r;
}else{
return (x.compareTo(r.data)<0) ? contains(x,r.left):contains(x,r.right);
}
}
红黑树的插入----自底向上插入
自底向上的插入中,RBTree的插入与BST的插入方式是一致的,只不过是在插入过后,可能会导致树的不平衡,这时就需要对树进行旋转操作和颜色修复(在这里简称插入修复),逐级向上修复,使得它符合RBTree的定义。
新插入的节点是红色的,插入修复操作如果遇到父节点的颜色为黑则修复操作结束。也就是说,只有在父节点为红色节点的时候是需要插入修复操作的。
插入修复操作分为以下的三种情况,镜像对称后总共六种,而且新插入的节点的父节点都是红色的:
-
叔叔节点也为红色。
-
叔叔节点为黑色,且祖父节点、父节点和新节点不处于一条斜线上。
-
叔叔节点为黑色,且祖父节点、父节点和新节点处于一条斜线上。
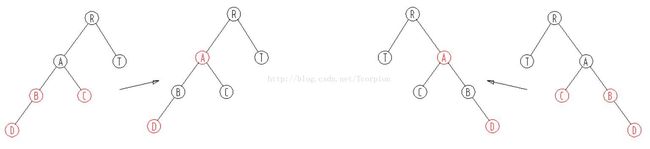
case1: 父节点红,叔叔节点红
将父节点和叔叔节点与祖父节点的颜色互换,这样就符合了RBTRee的定义。即维持了高度的平衡,修复后颜色也符合RBTree定义的第三条和第四条。下图中,操作完成后A节点变成了新的节点。如果A节点的父节点不是黑色的话,则继续做修复操作。
case2:父节点红,叔叔节点是黑色,且当前节点是右孩子
将父节点为根的子树右旋(左旋右旋的定义不一定和我的相同,按照下图描述为准),转换成case3,然后立即进行case3操作。
case3:父节点红,叔叔节点是黑色,当前节点是左孩子
将父节点为根的子树左旋(左旋右旋的定义不一定和我的相同,按照下图描述为准)操作。
/**
* @param x the added data node
* @param subRoot the subtree root
* @return the new subtree root
* */
private Node insert(Node x,Node subRoot){
if(nullNode==subRoot){
x.color=BLACK;
subRoot=x;
return subRoot;
}
Node last=nullNode,t=subRoot;
while(t!=nullNode){
last=t;
int compareValue=x.data.compareTo(t.data);
if(compareValue<0){
t=t.left;
}else if(compareValue>0){
t=t.right;
}else{
return subRoot;
}
}
x.parent=last;
if(last.data.compareTo(x.data)>0){
last.left=x;
}else{
last.right=x;
}
return subRoot;
}
/**
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的z
*/
private void insertFixUp(Node node) {
Node fix_parent, fix_gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while ( ((fix_parent = node.parent)!=nullNode) && (RED==fix_parent.color) ) {
fix_gparent = fix_parent.parent;
//若“父节点”是“祖父节点的左孩子”
if (fix_parent == fix_gparent.left) {
Node uncle = fix_gparent.right;
// Case 1条件:右叔叔节点是红色
if ( (uncle!=nullNode) && (RED==uncle.color) ) {
uncle.color=BLACK;
fix_parent.color=BLACK;
fix_gparent.color=RED;
node = fix_gparent;
continue;
}
// Case 2条件:右叔叔是黑色,且当前节点是右孩子
if ( (fix_parent.right == node) && (BLACK==uncle.color) ) {
Node tmp;
rightRotate(fix_parent);
tmp = fix_parent;
fix_parent = node;
node = tmp;
}
// Case 3条件:右叔叔是黑色,且当前节点是左孩子。
if ( (fix_parent.left == node) && (BLACK==uncle.color) ){
fix_parent.color=BLACK;
fix_gparent.color=RED;
leftRotate(fix_gparent);
}
} else { //若“z的父节点”是“z的祖父节点的右孩子”
Node uncle = fix_gparent.left;
// Case 4条件:左叔叔节点是红色
if ((uncle!=nullNode) && (RED==uncle.color)) {
uncle.color=BLACK;
fix_parent.color=BLACK;
fix_gparent.color=RED;
node = fix_gparent;
continue;
}
// Case 5条件:左叔叔是黑色,且当前节点是左孩子
if ( (fix_parent.left == node) && (BLACK==uncle.color) ) {
Node tmp;
rightRotate(fix_parent);
tmp = fix_parent;
fix_parent = node;
node = tmp;
}
// Case 6条件:左叔叔是黑色,且当前节点是右孩子。
if ( (fix_parent.right == node) && (BLACK==uncle.color) ) {
fix_parent.color=BLACK;
fix_gparent.color=RED;
rightRotate(fix_gparent);
}
}
}
// 将根节点设为黑色
this.root.color=BLACK;
} public void insert(AnyType x) {
//root=topDownInsert(x);
Node node=new Node<>(x,nullNode,nullNode,nullNode,RED);
root=insert(node,root);
insertFixUp(node);
return;
} 红黑树的插入----自顶向下插入
参考《数据结构与算法分析 JAVA语言描述》Weiss M.A中的描述,插入过程中需要自顶向下遍历,遍历的过程中将两种情况的红色进行上浮:1.左右儿子均为红色的进行颜色转换把红色上浮直至根,若根被上浮转换成红色,直接把根变黑;2.插入的儿子(红色)遇到红色的父亲,则进行旋转操作(同自底向上插入中的旋转)直到把红色上浮到根转为黑。
/**
* top-down insertion keep Red-Black balance
* @param x the inserted value
* @return the new root
* */
private Node topDownInsert(AnyType x) {
if(nullNode==root){
root=new Node<>(x,nullNode,nullNode,nullNode,BLACK);
header.right=root;
return root;
}
great=grand=parent=current=header;
while(compare(x,current)!=0){
great=grand;
grand=parent;
parent=current;
current=compare(x,current)<0?current.left:current.right;
if( (RED== current.left.color) && (RED== current.right.color) ){
handleReorient(x);
}
}
if(current!=nullNode){
return root;
}
current=new Node<>(x,nullNode,nullNode,parent,RED);
if(compare(x,parent)<0){
parent.left=current;
}else{
parent.right=current;
}
handleReorient(x);
return root;
}
//used in top-down insert routine
private Node header;
private Node current;
private Node parent;
private Node grand;
private Node great;
private final int compare(AnyType item ,Node node){
return (node==header)?1:((nullNode==node)?0:item.compareTo(node.data));
}
/**
* Internal routine that is called during an insertion
* if current has two red children or current inserted has a red parent.
* Performs a flip and rotations.
* @param item the item being inserted, the item has the same attribution of current.
* */
private void handleReorient(AnyType item){
//do the color flip
current.color=RED;
if(current.left!=nullNode && current.right!=nullNode){
current.left.color=BLACK;
current.right.color=BLACK;
}
//have to rotate
if(RED==parent.color){
grand.color=RED;
if( (compare(item,parent)<0) != (compare(item,grand)<0) ){//need double rotations.
parent=rotate(item,grand);
}
current=rotate(item,great);
current.color=BLACK;
}
header.right.color=BLACK;
}
/**
* Because the result is attached to the parent,the parent of the root of the rotated subtree is supposed as an input param.
* Called in handleReorient.
* @param item the item in handleReorient.
* @param parentOfRoot the parent of the root of the rotated subtree.
* @return the root of the rotated subtree.
*/
private Node rotate(AnyType item, Node parentOfRoot){
if(compare(item,parentOfRoot)<0){
parentOfRoot.left=compare(item,parentOfRoot.left)<0?leftRotate(parentOfRoot.left):rightRotate(parentOfRoot.left);
return parentOfRoot.left;
}else{
parentOfRoot.right=compare(item,parentOfRoot.right)<0?leftRotate(parentOfRoot.right):rightRotate(parentOfRoot.right);
return parentOfRoot.right;
}
}
红黑树的删除----自底向上删除
将红黑树内的某一个节点删除。需要执行的操作依次是:
首先,将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除;
然后,通过"旋转和重新着色"等一系列来修复操作修正该树,使之重新成为一棵红黑树。
自底向上删除详细描述如下:
第一步:将红黑树当作一颗二叉查找树,将节点删除。
case1: 被删除节点没有儿子(叶节点),直接将该节点删除就OK了。
case2: 被删除节点只有一个儿子,直接删除该节点,并用该节点的唯一子节点顶替它的位置与被删节点的父节点相连。
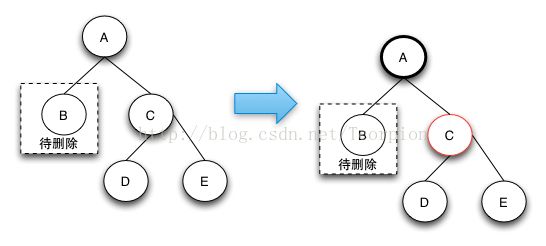
case3: 被删除节点有两个儿子,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点只可能是没有儿子的叶节点或者只有一个右儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性需要修复,即:①删除黑色节点会导致nullNode到根的黑色节点数不相同;②最终删除节点的儿子和最终删除的父亲相连时,若果这两个都是红色(删除的必定是黑色),则违背了红红不能连接和nullNode到根的黑色节点数相同这两项原则。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。删除操作修复的总体思想是从兄弟节点借调黑色节点使树保持局部的平衡,如果局部的平衡达到了,就看整体的树是否是平衡的,如果不平衡就接着向上追溯调整。
删除修复操作分为四种情况:
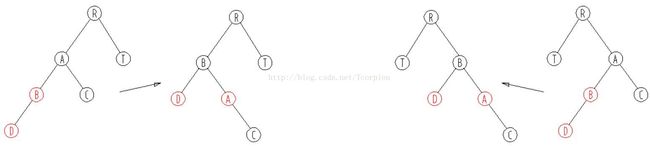
case1: 待删除的节点的兄弟节点是红色的节点;
case2: 待删除的节点的兄弟节点是黑色的节点,且兄弟节点的子节点都是黑色的;
case3: 待调整的节点的兄弟节点是黑色的节点,且兄弟节点的左子节点是红色的,右节点是黑色的(兄弟节点在右边),如果兄弟节点在左边的话,就是兄弟节点的右子节点是红色的,左节点是黑色的;
case4: 待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
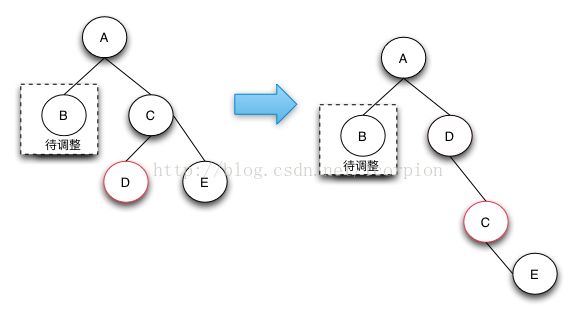
case1需要将兄弟节点提升到父节点,由于兄弟节点是红色的,根据RBTree的定义,兄弟节点的子节点是黑色的,就可以从它的子节点借调了。这样转换之后就会变成后面的case 2,case 3,或者case 4进行处理了。上升操作需要对C做一个左旋操作,如果是镜像结构的树只需要做对应的右旋操作即可。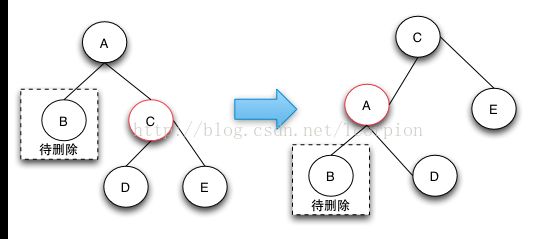
case 2的删除操作是由于兄弟节点可以消除一个黑色节点,因为兄弟节点和兄弟节点的子节点都是黑色的,所以可以将兄弟节点变红,这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点,继续向上调整,直到整颗树的颜色符合RBTree的定义为止。case 2这种情况下之所以要将兄弟节点变红,是因为如果把兄弟节点借调过来,会导致兄弟的结构不符合RBTree的定义,这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后,达到了局部的平衡了,但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点,接着进行修复操作。
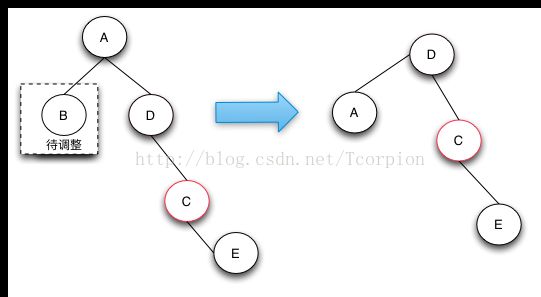
case 3的删除操作是一个中间步骤,它的目的是将左边的红色节点借调过来,这样就可以转换成case 4状态了,在case 4状态下可以将D,E节点都阶段过来,通过将两个节点变成黑色来保证红黑树的整体平衡。之所以说case-3是一个中间状态,是因为根据红黑树的定义来说,下图并不是平衡的,他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况,是因为可以通过借用侄子节点的红色,变成黑色来符合红黑树定义4.
Case 4的操作是真正的节点借调操作,通过将兄弟节点以及兄弟节点的右节点借调过来,并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的,这样的话,整棵树还是符合RBTree的定义的。Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑,且子节点不全部为黑,才有可能借调到两个节点来做黑节点使用,从而保持整棵树都符合红黑树的定义。
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。
/**
* 删除结点(node)
*
* 参数说明:
* node 删除的结点
*/
private void remove(Node node) {
Node child, parent;//最终删除点的child 和 parent
boolean color; //最终删除点的color
// 被删除节点的"左右孩子都不为空"的情况。
if ( (node.left!=nullNode) && (node.right!=nullNode) ) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
Node replace = node;
// 获取后继节点
replace = replace.right;
while (replace.left != nullNode)
replace = replace.left;
// node的父节点往下接node改为接replace
// "node节点"不是根节点(只有根节点不存在父节点)
if (node.parent!=nullNode) {
if ((node.parent).left == node)
(node.parent).left = replace;
else
(node.parent).right = replace;
} else {
// "node节点"是根节点,更新根节点。
this.root = replace;
}
// 提取replace信息
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace.right;
parent = replace.parent;
// 保存"取代节点"的颜色
color = replace.color;
/* case1:"被删除节点"它的后继节点恰好是其右儿子(是右子树的根)
* node
* / \
* left replace
*/
if (parent == node) {
parent = replace;
} else {
/* case2:"被删除节点"它的后继节点在右子树最左端(不是右子树的根)
* node
* / \
* left rightSubtree
* /
* parent
* /
* replace
* \
* child
*/
// child不为空
if (child!=nullNode)
child.parent = parent;
parent.left = child;
replace.right = node.right;
node.right.parent = replace;
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = nullNode;
return ;
}// end 被删除节点的"左右孩子都不为空"的情况。
/* "被删除节点"只有一个儿子或者没有儿子
* node
* /
* left
*/
if (node.left !=nullNode) {
//case3:"被删除节点"只有一个左儿子
child = node.left;
} else {
//case4 & 5:"被删除节点"只有一个右儿子 或者 无儿子
child = node.right;
}
parent = node.parent;
// 保存"取代节点"的颜色
color = node.color;
if (child!=nullNode)
child.parent = parent;
// "node节点"不是根节点
if (parent!=nullNode) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.root = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = nullNode;
}
/**
* 红黑树删除修正函数
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 内容讲解:
* 删除修复操作分为四种情况(删除黑节点后),镜像对称后为8种:
* 1.待删除的节点的兄弟节点是红色的节点。
* 2.待删除的节点的兄弟节点是黑色的节点,且兄弟节点的子节点都是黑色的。
* 3.待调整的节点的兄弟节点是黑色的节点,且兄弟节点的左子节点是红色的,右节点是黑色的(兄弟节点在右边),
* 如果兄弟节点在左边的话,就是兄弟节点的右子节点是红色的,左节点是黑色的。
* 4.待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
*
* 参数说明:
* @param node remove中最终删除的点的位置被child补上,此node实际是remove中的child取代.
* @param parent 为最终删除的点的parent,也是删除后的child的parent.
*
*/
private void removeFixUp(Node node, Node parent) {
Node brother;
while ((node==nullNode || node.color==BLACK) && (node != this.root)) {
if (parent.left == node) {
brother = parent.right;
if (brother.color==RED) {
// Case 1: x的兄弟w是红色的
brother.color=BLACK;
parent.color=RED;
rightRotate(parent);
brother = parent.right;
}
if ( (brother.left==nullNode || (brother.left.color==BLACK)) &&
(brother.right==nullNode || (brother.right.color==BLACK)) ) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
brother.color=RED;
node = parent;
parent = node.parent;
} else {
if (brother.right==nullNode || (brother.right.color==BLACK)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
brother.left.color=BLACK;
brother.color=RED;
leftRotate(brother);
brother = parent.right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
brother.color= parent.color;
parent.color=BLACK;
brother.right.color=BLACK;
rightRotate(parent);
node = this.root;
break;
}
} else {
brother = parent.left;
if (brother.color==RED) {
// Case 5: x的兄弟w是红色的
brother.color=BLACK;
parent.color=RED;
leftRotate(parent);
brother = parent.left;
}
if ((brother.left==nullNode || (brother.left.color==BLACK)) &&
(brother.right==nullNode || (brother.right.color==BLACK))) {
// Case 6: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
brother.color=RED;
node = parent;
parent = node.parent;
} else {
if (brother.left==nullNode || (brother.left.color==BLACK)) {
// Case 7: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
brother.right.color=BLACK;
brother.color=RED;
rightRotate(brother);
brother = parent.left;
}
// Case 8: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
brother.color=parent.color;
parent.color=BLACK;
brother.left.color=BLACK;
leftRotate(parent);
node = this.root;
break;
}
}
}
if (node!=nullNode)
node.color=BLACK;
}
参考文章和图片:
1.http://www.open-open.com/lib/view/open1481181302046.html
2.http://www.cnblogs.com/skywang12345/p/3624343.html