《剑指offer》面试题03:数组中重复的数字
更多剑指offer面试习题请点击: 《剑指offer》(第二版)题集目录索引
- 一、题目1
- 二、解题思路1
- 三、代码1
- 四、题目2
- 五、解题思路2
- 六、代码2
一、题目1
在一个长度为n的数组里的所有数字都在0~n-1的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
例如:
输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是重复的数字2或者3。
二、解题思路1
我们知道这个数组中的数字都在0~n-1范围内,假设这个数组中没有重复的数字,那把数组排序后数字i会出现在下标为i的位置。因为数组中有重复的数字,那么有的位置可能有多个数字,同时有些位置可能没有数字。
现在重排这个数组。从头到尾依次扫描数组中的数字。当扫描到下标为i的数字num[i]时,先比较num[i]是不是和他的下标i相等。是的话接着扫描下一个数字;
不是的话,那就再拿数字num[i]和下标为num[i]的数字(num[num[i])比较。如果num[i]和num[num[i]相等,那就找到了第一个重复的数字(这个数字num[i]在下标为i和下标为num[i] 的位置都出现了);
如果它和num[num[i]不相等,那就把第i个数字num[i]和第num个数字num[num[i]交换,把num[i](num [i]原先在位置 i处)放到属于它的位置。接下来再重复这个比较、交换的过程,直到找到一个重复的数字。
这个算法的保证能找出一个重复的数字(只要数组中有),但它的缺点是会改变数组的内容。
时间复杂度: O(n) O ( n )
空间复杂度: O(1) O ( 1 )
三、代码1
< code >
int duplicate(int* number, int length)
{
if (number == NULL || length <= 0)
{
return -1;
}
/* 判断数组是否符合规定 */
int i = 0;
for (i = 0; i < length; i++)
{
if (number[i] < 0 || number[i] > length - 1)
{
return -1;
}
}
for (i = 0; i < length; i++)
{
while (number[i] != i)
{
/*判断下标为i的元素和下标为number[i]的元素是否相等*/
if (number[i] == number[number[i]])
{
return number[i];
}
else
{
int tmp = number[i];
number[i] = number[tmp];
number[tmp] = tmp;
}
}
}
return -1;
}四、题目2
在一个长度为 n+1 的数组里的所有数字都在 1~n 的范围内,所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字,但不能修改输入的数组。例如,如果输入长度为8的数组{2, 3, 5, 4, 3, 2, 6, 7},那么对应的输出是重复的数字2或者3。
五、解题思路2
这里数组的长度是 n+1,而里面的数字的大小都在1 ~n 内,出于时间复杂度和空间复杂度考虑,这里采用一种类似于二分查找的算法。
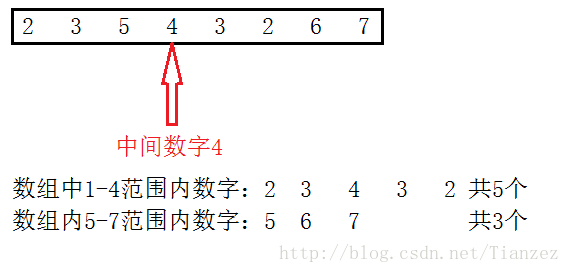
这里就以数组{2, 3, 5, 4, 3, 2, 6, 7}为例。
先找到中间大小元素 mid = (n-1)/2 + 1 = (7-1)/2 + 1 = 4;
然后把1~7的范围分成两部分:1~4 和 4~7;
再统计数组中1~4的数字出现的次数和5~7的数字出现的次数,从下面图片中我们可以看到:
1~4部分:数字1、2、3、4出现的次数共计5次;
5~7部分:数字5、6、7 出现的次数共计3次。
很明显1~4这部分有重复的数字。
我们再把1~4范围分成两部分:
1~2部分;数组中数字1或2出现了2次
3~4部分;数组中数字3或4出现了3次
所以3、4这两个数字一定有一个是重复的,最后再统计数字3和数字4在数组中出现的次数,很容易发现数字3在数组中出现了2次,所以找出重复出现的数字:3

这种方法不会改变数组的内容,但是并不能百分百找出重复的数字,例如数组{2, 1, 3, 1, 4},此时是找不到重复数字1的。所以此方法虽然效率极高,但不推荐使用。如果可以,推荐使用hash。
时间复杂度: O(nlogn) O ( n l o g n )
空间复杂度: O(1) O ( 1 )
注意:这样二分查找算法不能保证找出所有的重复数字,例如数组{1, 1, 2, 4, 5, 6, 7},利用二分查找法,分成两个区间[1, 4]和[5, 7],结果发现[1, 4]范围内的数字出现了4次,这是候此算法便失效了。
六、代码2
int getSize(const int* number, int length, int start, int end)
{
if (number == NULL)
{
return 0;
}
int count = 0;
int i = 0;
for (i = 0; i < length; i++)
{
if (number[i] >= start && number[i] <= end)
count++;
}
return count;
}
int getDuplicate(const int* number, int length)
{
if (number == NULL || length <= 0)
{
return -1;
}
int start = 1;
int end = length - 1;
int mid = 0;
while (end >= start)
{
mid = ((end - start) >> 1) + start;
int count = getSize(number, length, start, mid);
if (end == start)
{
if (count > 1)
{
return start;
}
else
{
break;
}
}
/* 重复数字出现在前半部分数组 */
if (count > (mid - start + 1))
{
end = mid;
}
else
{
/* 重复数字出现在前半部分数组 */
start = mid + 1;
}
}
return -1;
}