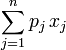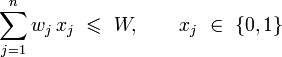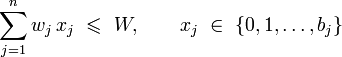无界背包问题
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。
相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。
也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?
定义
我们有n种物品,物品j的重量为wj,价格为pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。
如果限定每种物品只能选择0个或1个,则问题称为0-1背包问题。可以用公式表示为:
如果限定物品j最多只能选择bj个,则问题称为有界背包问题。可以用公式表示为:
如果不限定每种物品的数量,则问题称为无界背包问题。
各类复杂的背包问题总可以变换为简单的0-1背包问题进行求解。
无界背包问题 (物品数量不限)
如果重量w1, ..., wn和W都是非负的整数,那么用动态规划,可以用伪多项式时间解决背包问题。下面描述了无界背包问题的解法。
简便起见,我们假定重量都是正整数(wj > 0)。在总重量不超过W的前提下,我们希望总价格最高。对于Y ≤W,我们将在总重量不超过Y的前提下,总价格所能达到的最高值定义为A(Y)。A(W)即为问题的答案。
显然,A(Y)满足:
- A(0) = 0
- A(Y) = max { A(Y - 1), max { pj +A(Y - wj) | wj ≤ Y } }
其中,pj为第j种物品的价格。
关于第二个公式的一个解释:总重量为Y时背包的最高价值可能有两种情况,第一种是该重量无法被完全填满,这对应于表达式A(Y - 1)。第二种是刚好填满,这对应于一个包含一系列刚好填满的可能性的集合,其中的可能性是指当最后放进包中的物品恰好是重量为wj的物品时背包填满并达到最高价值。而这时的背包价值等于重量为wj物品的价值和当没有放入该物品时背包的最高价值之和。故归纳为表达式pj + A(Y - wj)。最后把所有上述情况中背包价值的最大值求出就得到了A(Y)的值。
如果总重量为0,总价值也为0。然后依次计算A(0), A(1), ..., A(W),并把每一步骤的结果存入表中供后续步骤使用,完成这些步骤后A(W)即为最终结果。由于每次计算A(Y)都需要检查n种物品,并且需要计算W个A(Y)值,因此动态规划解法的时间复杂度为O(nW)。如果把w1, ..., wn, W都除以它们的最大公因数,算法的时间将得到很大的提升。
尽管背包问题的时间复杂度为O(nW),但它仍然是一个NP完全问题。这是因为W同问题的输入大小并不成线性关系。原因在于问题的输入大小仅仅取决于表达输入所需的比特数。事实上,logW,即表达W所需的比特数,同问题的输入长度成线性关系。
下面例程实现上上述算法,A(0)~ A(Y)初始为0(即代码中value[ ]数组),在循环中不断计算 max { pj + A(Y -wj) | wj ≤ Y }
即,在实现时,A(Y) = max { A(Y - 1), max { pj +A(Y - wj) | wj ≤ Y } } 被简化为A(Y) = max { pj + A(Y - wj) | wj ≤ Y } ,
A(Y - wj) 就是表示最大承重Y - wj的背包最多填充物品值,不是恰好有Y -wj重量的物品,而是不超过Y - wj重量的物品,再多也塞不下了。
// KnapsackProblem.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
#include
#include
using namespace std;
#define MAX 8
#define MIN 1
class Fruit
{
private:
string name;
int size;
int price;
public:
Fruit(string name,int size,int price)
{
this->name=name;
this->size=size;
this->price=price;
}
string getName(){
return name;
}
int getPrice(){
return price;
}
int getSize(){
return size;
}
};
void main()
{
int item[MAX+1];
int value[MAX+1];
Fruit fruits[]={
Fruit("李子", 4, 4500),
Fruit("苹果", 5, 4700),
Fruit("橘子", 2, 2250),
Fruit("草莓", 1, 1100),
Fruit("甜瓜", 6, 3700),
Fruit("菠萝", 2, 4900),
Fruit("西瓜", 3, 5800)
};
for (int i = 0; i < MAX+1; i++)
{
item[i] = 0;
value[i] = 0;
}
for(int i = 0; i < 7; i++)
{
for(int s = fruits[i].getSize();s <= MAX; s++)
{
//s表示现在背包的大小
int p = s-fruits[i].getSize(); //表示每次增加单位背包空间,背包所剩的空间
int newvalue = value[p] + fruits[i].getPrice(); //value[p]表示增加的背包空间可以增加的价值,fruits[i].getprice()表示原有的背包的价值
if(newvalue > value[s])
{
//现有的价值是否大于背包为s时的价值
value[s] = newvalue;
item[s] = i;//将当前的水果项添加到背包的物品中
}
}
}
cout<<"物品\t价格"< MIN; i = i - fruits[item[i]].getSize())
{
cout<