线性回归模型(Linear regression model)
绪论
在开始之前,先大致说明下机器学习中的一些大的概念及分类。
机器学习中的学习算法很多,包括线性回归、逻辑回归、随机森林、决策树、聚类、贝叶斯等等。但是这些学习算法可以归为两类,即监督学习(supervised learning)和非监督学习(unsupervised learning);如果更加细分的话还有半监督学习。
那么监督学习和非监督学习有什么区别呢,所谓的监督学习就是学习中有训练集,知道输入与输出之间的关系,输入数据有标签,实际上机器学习算法中半数以上的算法属于监督学习,比如逻辑回归、随机森林、神经网络等等;非监督学习中无训练样本,处理的是无标签数据,按照性质自动分组,典型的非监督学习的算法是聚类、主成分分析(PCA)。
监督学习又可以分为两类,一种是回归(regression),另一种是分类(classificetion)。回归的输出值是连续的,下文将结合吴恩达在Coursera上的Machine Learning中的房价预测的例子进行说明;分类是输出值则是离散的,比如垃圾邮件分类,图像识别(输入一张动物的图片,输出这张图片中 的动物到底属于什么,小狗,小猫还是猴子或者其他),分类又分为二分类和多分类,垃圾邮件的分类就是二分类问题,一封邮件要么是垃圾邮件要么是非垃圾邮件,不会存在第三种情况;而图像识别小动物还就是属于多分类的问题。二分类和多分类实际上就是根据输出变量y的取值决定的,如果y取值只能取{0,1},那么这就是二分类问题,如果y取值为{0,1,2,3},每个取值代表不同的情况,比如y= 0时代表小狗,y = 1时代表小猫,y = 2时代表猴子,y= 3 时代表其他,那么这就属于多分类问题。分类是监督学习中的主要研究问题。
本文采用下标表示属性(特征),上标表示样本的标记方法,例如![]() 表示第1个属性值(特征值),
表示第1个属性值(特征值),![]() 表示第1个样本,而
表示第1个样本,而![]() 则表示第i个样本的第j个属性。
则表示第i个样本的第j个属性。
假设样本示例有n个属性 ![]() ,其中
,其中![]() 表示
表示![]() 在第i个属性上的取值,线性模型试图学得一个通过属性的线性组合来进行预测的函数,即
在第i个属性上的取值,线性模型试图学得一个通过属性的线性组合来进行预测的函数,即
![]()
向量的表示形式为: ![]()
其中![]() 。训练模型的过程就是确定参数
。训练模型的过程就是确定参数![]() 和b的过程。
和b的过程。![]() 是样本
是样本![]() 中各个属性的权重,
中各个属性的权重,![]() 的值越大,表示属性i的权重越大,即属性i在预测中越重要。
的值越大,表示属性i的权重越大,即属性i在预测中越重要。
目录
绪论
线性回归模型
梯度下降法
最小二乘法(least square method)
最小二乘法与梯度下降法的区别
线性回归的应用
线性回归模型
线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记。假设有数据集![]() ,这里假设所有样本只有一个属性值,线性回归就是对数据样本进行训练学习得出假设函数
,这里假设所有样本只有一个属性值,线性回归就是对数据样本进行训练学习得出假设函数![]() ,使得
,使得![]() 。前面提到,训练模型的过程就是确定参数
。前面提到,训练模型的过程就是确定参数![]() 和b的过程。我们的目的是使训练学习得到的函数
和b的过程。我们的目的是使训练学习得到的函数![]() 和样本的输出标签
和样本的输出标签![]() 尽可能的相近,现在问题的关键就是怎么衡量
尽可能的相近,现在问题的关键就是怎么衡量![]() 和
和![]() 之间的相近程度。为此,我们有以下定义:
之间的相近程度。为此,我们有以下定义:
称![]() 为代价函数或者均方误差。我们要做的就是找到
为代价函数或者均方误差。我们要做的就是找到![]() 及
及![]() ,使得
,使得![]() 最小。 均方误差函数的几何意义:
最小。 均方误差函数的几何意义:
在上图中蓝线为![]() ,X表示是样本点,
,X表示是样本点,![]() 就是实际输出值
就是实际输出值![]() 和预测值
和预测值![]() 之间的距离和求平均。
之间的距离和求平均。![]() 是为了求导时与平方项2相消。
是为了求导时与平方项2相消。
接下来的就是对求出参数![]() 和参数
和参数![]() ,使得
,使得![]() 最小,最小化
最小,最小化![]() 常用的方法有两种:梯度下降法和最小二乘法
常用的方法有两种:梯度下降法和最小二乘法
梯度下降法
梯度下降法(gradient descent)是一种常用的一阶优化方法,其表达式为
其中![]() 为学习参数,为正数,其控制更新参数
为学习参数,为正数,其控制更新参数![]() 的幅度。为了方便理解,通过下图进行分析说明,为了简化问题,假设
的幅度。为了方便理解,通过下图进行分析说明,为了简化问题,假设![]() ,由
,由![]() 的定义知道
的定义知道![]() 是关于
是关于![]() 的二次函数,其几何图像是开口向上的二次抛物线。
的二次函数,其几何图像是开口向上的二次抛物线。
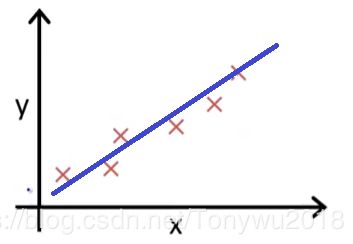
假设初始点omega在最优点的右侧即为蓝色的点,绿色的直线表示在点omega处的切线,由图所示,切线斜率为正,则![]() 为正,此时有
为正,此时有
其中学习参数![]() ,
,![]() ,那么
,那么![]() ,
,![]() 减去一个大于0的数,会使
减去一个大于0的数,会使![]() 本身减小,也就是说经过一次迭代更新后
本身减小,也就是说经过一次迭代更新后![]() 变小,反应到上面的图像上就是
变小,反应到上面的图像上就是![]() 左移,对于
左移,对于![]() 来说它是减小的,依次类推,经过多次迭代更新后,初始的
来说它是减小的,依次类推,经过多次迭代更新后,初始的![]() 会到达黑色点处,这时
会到达黑色点处,这时![]() 是最小的,而这时候的
是最小的,而这时候的![]() 就是我们最后想要得到的参数值
就是我们最后想要得到的参数值![]() 。我们可以看到,随着
。我们可以看到,随着![]() 值的不断减小,
值的不断减小,![]() 在
在![]() 处的切线斜率也会变小,即
处的切线斜率也会变小,即![]() 减小,如果
减小,如果![]() 值不变的话,那么
值不变的话,那么![]() 每次迭代更新的幅度会变小。当
每次迭代更新的幅度会变小。当![]() 到达最低点处,
到达最低点处,![]() 在
在![]() 处的切线斜率为0,也就是
处的切线斜率为0,也就是![]() 为0,此时
为0,此时![]() ,也就是说
,也就是说![]() 不会再更新,会收敛到使得
不会再更新,会收敛到使得![]() 取最小值的点。
取最小值的点。
同样的,我们假设初始点theta1在最优点的左侧,同样是蓝色的点,如下图:
这时,切线斜率为负数,![]() 为负数,
为负数,![]() ,那么
,那么![]() ,
,![]() 减去一个小于0的数,会使
减去一个小于0的数,会使![]() 本身增大,也就是说经过一次迭代更新后
本身增大,也就是说经过一次迭代更新后![]() 变大,反映到图像上就是
变大,反映到图像上就是![]() 右移,此时对于
右移,此时对于![]() 来说同样是减小的。经过多次迭代更新,
来说同样是减小的。经过多次迭代更新,![]() 会达到使得
会达到使得![]() 最小的点
最小的点![]() 处。,同样会在
处。,同样会在![]() 处收敛。
处收敛。
学习参数![]() 的选择是梯度下降中一个关键的问题,如果
的选择是梯度下降中一个关键的问题,如果![]() 设置的过大,那么经过一次迭代更新后,
设置的过大,那么经过一次迭代更新后,![]() 会直接越过最低值的点,最后不会收敛,如果
会直接越过最低值的点,最后不会收敛,如果![]() 的值太小,那么每次更新的幅度会很小,会导致梯度下降的速度变的很慢。一般情况下
的值太小,那么每次更新的幅度会很小,会导致梯度下降的速度变的很慢。一般情况下![]() 取值会在0.01-1之间,最常用的
取值会在0.01-1之间,最常用的![]() 值为0.1。
值为0.1。
上面是在简化了![]() 的情况下进行的说明。那么在更一般的情况下,同样也是可以的。
的情况下进行的说明。那么在更一般的情况下,同样也是可以的。
一个样本可能有很多特征,以吴恩达老师在Coursera上房价预测为例,输入变量(也称特征向量)x的特征可能包括房子的面积、房子所在的楼层、房子的地段等等,这些特征共同决定了样本的输出变量(也称目标变量)y,其实也就是房子的价格。当一个样本中的特征比较多时,那么特征之间的范围如果差距比较大,会使得梯度下降的速度减慢。那么怎么解决这个问题呢,可以使用特征缩放(feature scaling)的方法,最常用的特征缩放是均值归一化(mean normalization),这会把特征控制在大致相同的范围。
其中![]() 表示第i个特征变量,
表示第i个特征变量,![]() 为第i个特征的平均值,
为第i个特征的平均值,![]() 为第i个特征值的标准差。实际上,特征缩放属于特征工程中的内容,以后会写有关特征工程相关的内容。
为第i个特征值的标准差。实际上,特征缩放属于特征工程中的内容,以后会写有关特征工程相关的内容。
最小二乘法(least square method)
代价函数实际上是多元函数,在无约束条件下最小化多元函数这种问题在高数下册“多元函数微分学”一章中学过,最小二乘法实际上就是我们比较熟悉的把函数![]() 对各个变量求偏导数,然后令其为0,最后解出
对各个变量求偏导数,然后令其为0,最后解出![]() 和b。
和b。
![]()
其中X为矩阵:
![]() ,其中
,其中![]() 。最小二乘法的详细推导过程在周志华老师的西瓜书中有,这里不做详细说明。
。最小二乘法的详细推导过程在周志华老师的西瓜书中有,这里不做详细说明。
最小二乘法与梯度下降法的区别
作为最小化代价函数的两种常用方法,什么时候使用最小二乘法,什么时候使用梯度下降法呢,那么我们需要对这两种方法进行对比。
| 方法 | 优点 | 缺点 | 复杂度 |
| 梯度下降法 | 当特征数较多时,工作效率高 | 需要选择学习参数 |
|
| 最小二乘法 | 不需要特征缩放 不需要选择学习参数 不需要迭代 |
当特征数n比较大时,运行速度慢 |
通常在线性回归模型中一般使用梯度下降的方法最小化代价函数。
线性回归的应用
为了方便理解理论知识,以梯度下降的方法为例,使用的是吴恩达老师房价预测的例子。对代价函数进行最小化。本例使用的是Python编写。
下图是线性模型拟合离散的数据点的可视化结果
下图是迭代次数与代价函数之间的函数关系,可以看到当迭代次数到200次左右的时候,代价函数就几乎不再下降。
下图是一个三维图形,曲面高度表示![]() 的大小,可以看到
的大小,可以看到![]() 位置处对应的
位置处对应的![]() 值最小
值最小
下图是二维轮廓图,类似于地理中的等高线,可以看到在![]() 最低处,
最低处,![]() 。
。
参考文献:
1、吴恩达老师在Coursera上的Machine Learning课程 https://www.coursera.org/learn/machine-learning
2、周志华老师《机器学习》
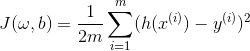

![X =\left[ \begin{matrix} \vec x^{(1)T} & 1 \\\vec x^{(2)T} & 1\\ ...\\\vec x^{(m)T} & 1 \end{matrix} \right ]\tag{1}](http://img.e-com-net.com/image/info8/94d44b1dafeb47d3ab000ba8c8149863.gif)




