二分图匹配及匈牙利算法的全面讲解及python实现

1、背景

在生活中常常遇到两组元素多对多匹配而又数目有限的情况，我们需要对其进行最大匹配数的分配，使效率最大化。例如，有一组压缩气缸和一组压缩活塞，每一个型号的压缩气缸有一个固定的内径大小，每一个型号的压缩活塞可以匹配内径在一定范围内的气缸，使用匈牙利算法得到活塞和气缸对大匹配数的方案。

2、二分图定义

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边(i，j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i∈ A,j∈ B)，则称图G为一个二分图。选择这样的子集中边数最大的子集称为图的最大匹配问题。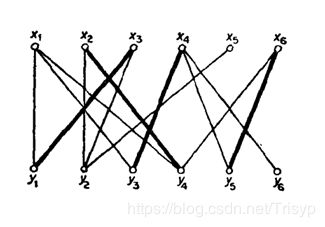

二分图匹配是很常见的算法问题，一般用匈牙利算法解决二分图最大匹配问题。

 

3、匹配定义

匹配：M是G的一个匹配，(M：{ (x2,y4),(x3,y1),(x4,y3),(x6,y5)})

M-交错路：p是G的一条通路，如果p中的边为不属于M但属于G中的边与属于M中的边交替出现，则称p是一条M-交错路。即从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边、...形成的路径。例如:x1-y3-x2-y3。

M-饱和点：对于v∈V(G)，如果v与M中的某条边关联，则称v是M-饱和点，否则称v是非M-饱和点。如x2,x3,x4,x6,y1,y3,y4,y5都属于M-饱和点，而其它点都属于非M-饱和点。

M-可增广路：p是一条M-交错路，如果p的起点和终点都是非M-饱和点，则称p为M-可增广路。即从一个未匹配点出发，走交替路，途径另一个未匹配点（出发的点不算）。如:x1-y1-x3-y2

由增广路的定义可以推出下述三个结论:

    1. P的路径个数必定为奇数，第一条边和最后一条边都不属于M。

    2. 将M和P进行取反操作可以得到一个更大的匹配M'。

    3. M为G的最大匹配当且仅当不存在M的增广路径。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

完备匹配：如果一个匹配中，|A|<=|B|且匹配数|M|=|A|则称此匹配为完全匹配，也称作完备匹配。特别的当|A|=|B|称为完美匹配。

即|A|≠|B|的二分图一定没有完全匹配，正则的|A|=|B|的二分图一定有完全匹配。

4、最大匹配与最小点覆盖
最小点覆盖：假如选了一个点就相当于覆盖了以它为端点的所有边，你需要选择最少的点来覆盖所有的边

最小割定理是一个二分图中很重要的定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

最小点集覆盖==最大匹配的证明。首先，最小点集覆盖一定>=最大匹配，因为假设最大匹配为n，那么我们就得到了n条互不相邻的边，光覆盖这些边就要用到n个点。现在我们来思考为什么最小点集覆盖一定<=最大匹配。任何一种n个点的最小点集覆盖，一定可以转化成一个n的最大匹配。因为最小点集覆盖中的每个点都能找到至少一条只有一个端点在点集中的边（如果找不到则说明该点所有的边的另外一个端点都被覆盖，所以该点则没必要被覆盖，和它在最小点集覆盖中相矛盾），只要每个端点都选择一个这样的边，就必然能转化为一个匹配数与点集覆盖的点数相等的匹配方案。所以最大匹配至少为最小点集覆盖数，即最小点集覆盖一定<=最大匹配。综上，二者相等。

现在要用匈牙利算法找出最多能发展几对。

5、匈牙利算法

求最大匹配的一种显而易见的算法是:先找出全部匹配，然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级函数。因此，需要寻求一种更加高效的算法。

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。如果我们置换增广路径中的匹配边和非匹配边，由于增广路径的首尾是非匹配点，其余则是匹配点，这样的置换不会影响原匹配中其他的匹配边和匹配点，因而不会破坏匹配；亦即增广路径的置换，可以得到比原有匹配更大的匹配（具体来说，匹配的边数增加了1）。

算法大致思路：⑴ 置M为空；

    ⑵ 找出一条增广路径P，通过异或操作获得更大的匹配M'代替M

    ⑶ 重复⑵操作直到找不出增广路径为止

由于二分图的最大匹配必然存在（比如，上限是包含所有顶点的完全匹配），所以，再任意匹配的基础上，如果我们有办法不断地搜寻出增广路径，直到最终我们找不到新的增广路径为止，我们就有可能得到二分图的一个最大匹配。这就是匈牙利算法的核心思想。唯一的问题在于，在这种贪心的思路下，我们如何保证不存在例外的情况，即：当前匹配不是二分图的最大匹配，但已找不到一条新的增广路径。

如何快速找出增广路：如下图所示，找一个非M-饱和点，画一棵M-交错树，如果能找到，就重复（2），不能找到算法就可以结束。

算法的证明（反证法）：

假设存在这样的情况：当前匹配不是二分图的最大匹配，但已找不到一条新的增广路径。因为当前匹配不是二分图的最大匹配，那么在两个集合中，分别至少存在一个非匹配点。那么情况分为两种：

1. 这两个点之间存在一条边：那么我们找到了一条新的增广路径，产生矛盾；

2. 这两个点之间不存在直接的边，即这两个点分别都只与匹配点相连，那么：

1) 如果这两个点可以用已有的匹配点相连，那么我们找到了一条新的增广路径，产生矛盾；

2) 如果这两个点无法用已有的匹配点相连，那么这两个点也就无法增加匹配中边的数量，也就是我们已经找到了二分图的最大匹配，产生矛盾。

综上，在所有可能的情况，上述假设都会产生矛盾。因此假设不成立，亦即贪心算法必然能求得最大匹配的解。

算法详细步骤:
              1.任意取一个匹配M（可以是空集或者只有一条边）

              2.令S是非饱和点（尚未匹配的点）的集合

              3.如果S是空集，则M已经是最大匹配

              4.从S中取出一个非饱和点u0作为起点，从此起点走交错路P

              5.如果P是一个增广路，则令M=M⊕P=(M-P)∪(P-M)

              6.如果P都不是增广路，则从S中去掉u0，转到步骤3

 

5、python程序

5.1 递归方法

class DFS_hungary():

    # 参数初始化

    def __init__(self, set_A, set_B, edge, cx, cy, visited):

        self.set_A, self.set_B = set_A, set_B  # 顶点集合

        self.edge = edge  # 顶点是否连边

        self.cx, self.cy = cx, cy  # 顶点是否匹配

        self.visited = visited  # 顶点是否被访问

        self.M = []  # 匹配

        self.res = 0  # 匹配数



    # 遍历顶点A集合，得到最大匹配

    def max_match(self):

        for i in self.set_A:

            if self.cx[i] == -1:  # 未匹配

                for key in self.set_B:  # 将visited置0表示未访问过

                    self.visited[key] = 0

                self.res += self.path(i)

                print('i', i, 'M',self.M)



    # 增广路置换获得更大的匹配

    def path(self, u):

        for v in self.set_B:

            if self.edge[u][v] and (not self.visited[v]):  # 如果可连且未被访问过

                self.visited[v] = 1 # 访问该顶点

                if self.cy[v] == -1:  # 如果未匹配， 则建立匹配

                    self.cx[u], self.cy[v] = v, u

                    self.M.append((u, v))

                    return 1

                else:

                    self.M.remove((self.cy[v], v))  # 如果匹配则删除之前的匹配

                    if self.path(self.cy[v]):  # 递归调用

                        self.cx[u], self.cy[v] = v, u

                        self.M.append((u, v))

                        return 1

            print('v', v, 'M', self.M)

        return 0





if __name__ == '__main__':

    set_A, set_B = ['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H']

    edge = {'A': {'E': 1, 'F': 0, 'G': 1, 'H': 0}, 'B': {'E': 0, 'F': 1, 'G': 0, 'H': 1},

            'C': {'E': 1, 'F': 0, 'G': 0, 'H': 1}, 'D': {'E': 0, 'F': 0, 'G': 1, 'H': 0}}  # 1表示可以匹配，0表示不能匹配

    cx, cy = {'A': -1, 'B': -1, 'C': -1, 'D': -1}, {'E': -1, 'F': -1, 'G': -1, 'H': -1}

    visited = {'E': 0, 'F': 0, 'G': 0, 'H': 0}

    dh = DFS_hungary(set_A, set_B, edge, cx, cy, visited)

    dh.max_match()

    print('res', dh.res)

    print('cx', cx)

    print('cy', cy)

    print('visited', visited)

# 结果显示：

# i A M [('A', 'E')]  # 对于E点，可与A点连接，第一次匹配，直接在max_match打印，存在增广路：CEAG

# v E M [('A', 'E')]  # 对于E点，不能和B点连接，在path中打印

# i B M [('A', 'E'), ('B', 'F')]  # 对于F点，可与B点连接，直接在max_match打印，匹配数增加，存在增广路：CEAG

# v E M [('B', 'F')]  # 对于E点，可以与C连接，但已经与A点连接，从M中移除AE，在path中打印，进入递归内部

# v F M [('B', 'F')]

# i C M [('B', 'F'), ('A', 'G'), ('C', 'E')]  # 对于G点，可与A点连接，直接在max_match打印，匹配数增加，存在增广路：DGAECH

# v E M [('B', 'F'), ('A', 'G'), ('C', 'E')]  # 对于E点，不能与D点连接，在path中打印

# v F M [('B', 'F'), ('A', 'G'), ('C', 'E')]  # 对于F点，不能与D点连接，在path中打印

# v E M [('B', 'F')]  # 对于G点，可以与D连接，但已经与A点连接，从M中移除AG，在path中打印，进入递归内部，继续移除CE

# v F M [('B', 'F')]

# v G M [('B', 'F')]

# i D M [('B', 'F'), ('C', 'H'), ('A', 'E'), ('D', 'G')] # 无增广路

# res 4

# cx {'A': 'E', 'B': 'F', 'C': 'H', 'D': 'G'}

# cy {'E': 'A', 'F': 'B', 'G': 'D', 'H': 'C'}

# visited {'E': 1, 'F': 0, 'G': 1, 'H': 1}

5.2 非递归方法

class BFS_hungary(object):

    def __init__(self, graph):

        self.g = graph  # 无向图的矩阵表示

        self.Nx = len(graph)  # 顶点集A的个数

        self.Ny =  len(graph[0])  # 顶点集B的个数

        self.Mx = [-1]*self.Nx  # 初始匹配

        self.My = [-1]*self.Ny  # 初始匹配

        self.chk=[-1] * max(self.Nx,self.Ny)  # 是否匹配

        self.Q = []



    def Max_match(self):

        res=0  # 最大匹配数

        self.Q = [0 for i in range(self.Nx*self.Ny)]

        prev=[0] * max(self.Nx,self.Ny)  # 是否访问

        for i in range(self.Nx):

            if self.Mx[i]==-1:  # A中顶点未匹配

                qs=qe=0

                self.Q[qe]=i

                qe+=1

                prev[i]=-1

                flag=0

                while(qsand not flag):

                    u=self.Q[qs]

                    for v in range(self.Ny):

                        if flag:continue

                        if self.g[u][v] and self.chk[v]!=i:  #

                            self.chk[v]=i

                            self.Q[qe]=self.My[v]

                            qe+=1

                            if self.My[v]>=0: #

                                prev[self.My[v]]=u

                            else:

                                flag=1

                                d,e=u,v

                                while d!=-1:  # 将原匹配的边去掉加入原来不在匹配中的边

                                    t=self.Mx[d]

                                    self.Mx[d]=e

                                    self.My[e]=d

                                    d=prev[d]

                                    e=t

                    qs+=1

                if self.Mx[i]!=-1:  # 如果已经匹配

                    res+=1

        return res





if __name__ == '__main__':

    g = [[1, 0, 1, 0], [0, 1, 0, 1], [1, 0, 0, 1], [0, 0, 1, 0]]

    mm = BFS_hungary(g)

    print('res', mm.Max_match())

 

两个版本的时间复杂度均为O(V*E)。

DFS 的优点是思路清晰、代码量少，但是性能不如 BFS。测试了两种算法的性能。对于稀疏图，BFS 版本明显快于 DFS 版本；而对于稠密图两者则不相上下。

要点：

1. 从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。

1） 如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数+1，停止搜索。

2） 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。

2. 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS版本通过函数调用隐式地使用一个栈，而BFS版本使用prev数组。

 

 

文章参考地址：

算法思路讲的很清晰：https://liam0205.me/2016/04/03/Hungarian-algorithm-in-the-maximum-matching-problem-of-bigraph/

python代码实现：https://www.cnblogs.com/jamespei/p/5555734.html