阵列信号处理--基础概念

假设一平面波传播方向为\(\mathbf{a}\)，频率为\(w\),那么经过空间中的麦克风阵列系统处理后，可以得到该麦克风阵列对平面波的响应为

\[y(t,\mathbf{k})=\mathbf{H}^T\mathbf{v}_{k}(\mathbf{k})e^{jwt} \]

其中\(\mathbf{H}\)表示的是滤波器冲激响应的傅里叶变换，\(\mathbf{k}\)表示波数，其幅度最大值为\(\lvert\mathbf{k}\rvert=\frac{2\pi}{\lambda}\)，\(\mathbf{v}_{k}\)表示阵列波形矢量，可以表示成

\[\mathbf{v}_{k}(\mathbf{k})=\left[\begin{matrix} e^{-\mathbf{k^Tp_{0}}}\\e^{-\mathbf{k^Tp_{1}}}\\\vdots\\e^{-\mathbf{k^Tp_{N-1}}} \end{matrix} \right] \]

然后对\(y(t,\mathbf{k})\)进行傅里叶变换，可以得到

\[\mathbf{Y}(w,\mathbf{k})=\mathbf{H}^{T}(w)\mathbf{v}_{k}(\mathbf{k}) \]

将后面这一项定义为\(\Upsilon(w,\mathbf{k})\),即阵列的频率-波数响应函数，描述了一个阵列对于波数 \(\mathbf{k}\)，时频频率\(w\)的输入平面波的复增益。

\[\Upsilon(w,\mathbf{k})=\mathbf{H}^T(w)\mathbf{v}_{k}(\mathbf{k}) \]

波束方向图是用入射方向表示的频率-波数响应函数，可以将其表示成

\[B(w;\theta,\phi)=\Upsilon(w,\mathbf{k})\rvert_{\mathbf{k}=\frac{2\pi}{\lambda}\mathbf{a}(\theta,\phi)} \]

定义一个复数加权矢量为

\[\mathbf{w}^{H}[w_{0}^{*},\cdots,w_{N-1}^{*}] \]

那么\(y(t,\mathbf{k})\)可以表示成

\[y(t,\mathbf{k})=\mathbf{w}^{H}\mathbf{v}_{k}(\mathbf{k})e^{jwt} \]

此时

\[\Upsilon(w,\mathbf{k})=\mathbf{w}^T(w)\mathbf{v}_{k}(\mathbf{k}) \]

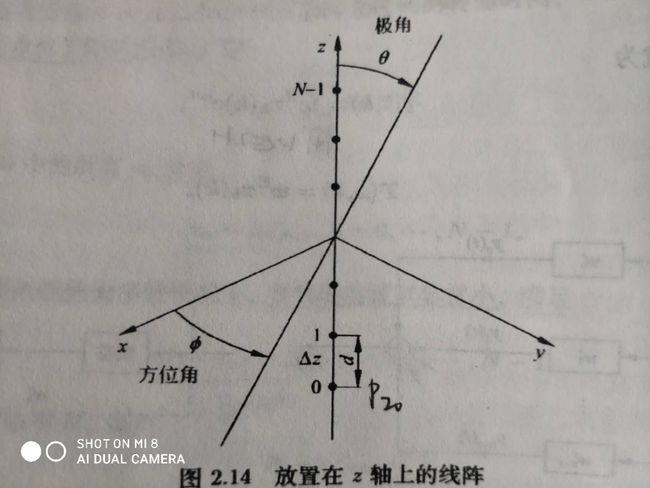
对于均匀线阵而言

，\(\mathbf{v}_{k}(\mathbf{k})\)可以表示成

\[\mathbf{v}_{k}(k)=[e^{j\frac{N-1}{2}\mathbf{k}_{z}d},e^{j(\frac{N-1}{2}-1)\mathbf{k}_{z}d},\cdots,e^{-j\frac{N-1}{2}\mathbf{k}_{z}d}]^T \]

其中\(\mathbf{k}_z=-\frac{2\pi}{\lambda}cos\theta\),那么此时的\(\Upsilon(w,k_z)\)可以表示成

\[\Upsilon(w,k_z)=\mathbf{w}^H\mathbf{v}_{k}(k)\\=\sum_{n=1}^{N-1}w_{n}^{*}e^{-j(n-\frac{N-1}2)k_zd} \]

令\(\psi=-k_zd=\frac{2\pi}{\lambda}dcos\theta=\frac{2\pi}{\lambda}du_z\),进而可以将\(\Upsilon(w,k_z)\)表示成

\[\Upsilon(w,k_z)=e^{-j\frac{N-1}{2}\psi}\sum_{n=1}^{N-1}w_{n}^{*}e^{jn\psi} \]

波数方向图可以表示为

\[B(\psi)=e^{-j\frac{N-1}{2}\psi}\sum_{n=1}^{N-1}w_{n}^{*}e^{jn\psi} \]

对于均匀加权线阵而言，此时\(w_n=\frac{1}{N}\),那么\(\Upsilon(w,k_z)\)和\(B(\psi)\)可以表示成

\[\Upsilon(\psi)=\frac{1}{N}\frac{sin(N\frac{\psi}{2})}{sin(\psi/2)}\\B(u)=\frac{1}{N}\frac{sin(\frac{\pi Nd}{\lambda}u)}{sin(\frac{\pi d}{\lambda}u)} -1\le u\le1 \]

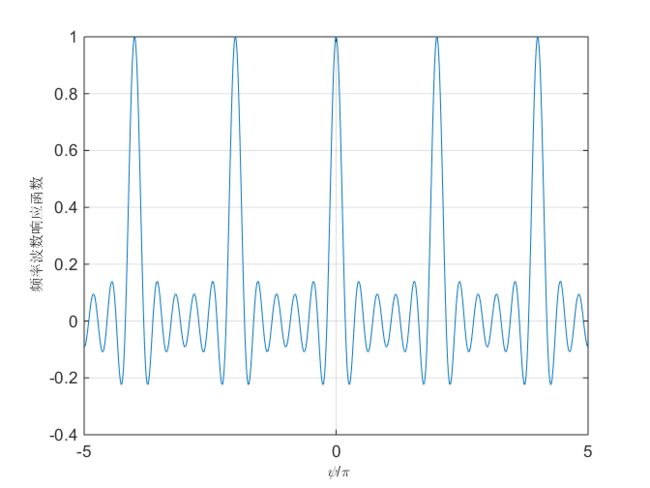
可以得出\(\Upsilon(\psi)\)是一个周期函数，当N是奇数的时候，其周期为\(2\pi\)，当N是偶数的时候，其周期为\(4\pi\)，对于任意的N值，其周期为\(2\pi\)，下图给出了当\(N=11\)的时候，\(\Upsilon(\psi)\)的变化趋势。

下面分析波束方向图的几个重要参数

• 3dB带宽(HPBW)
• 到第一零点的距离
• 到第一个旁瓣的距离
• 第一旁瓣的高度
• 其余零点的位置旁瓣衰减的速率
• 栅瓣

对于波束方向图

\[B(u)=\frac{1}{N}\frac{sin(\frac{\pi Nd}{\lambda}u)}{sin(\frac{\pi d}{\lambda}u)} -1\le u\le1 \]

（1）3dB带宽：定义为使\(\lvert B(\psi)\rvert^2=0.5\)的点。

（2）第一零点：方向图的零点出现在\(B(\psi)\)的分子为0而分母不为0的时候，则零点的出现满足下面的两个条件

\[\frac{\pi Nd}{\lambda}u=m\pi,m=1,2,\cdots.\\ \Rightarrow u=m\frac{\lambda}{Nd}\\u \neq \frac{\lambda}{d} \]

那么第一个零点出现的位置就是\(u=\frac{\lambda}{Nd}\),那么定义\(\Delta u_2=2\frac{\lambda}{Nd}\)为零点-零点波束宽度(BWNN)，该值的一半(0.5BWNN)是到第一零点的距离，这个值衡量了阵列分辨两个不同平面波的能力，即瑞利限。如果第二个波束方向图的峰值在第一个波束方向图的第一零点之外，那么就称这个平面波是可以被分辨的。

(3)旁瓣位置：旁瓣极大值出现的位置在当分子出现极大值的时候，即

\[sin(\frac{\pi Nd}{\lambda}u)=1 \]

可以得到解

\[u=\pm \frac{2m+1}{N}\frac{\lambda}{2d} \]

(4)栅瓣：栅瓣就是和主瓣波束一样高的波瓣。栅瓣出现分子和分母均为0的时候，栅瓣出现的间隔为

\[u=m.\frac{\lambda}{d} \]

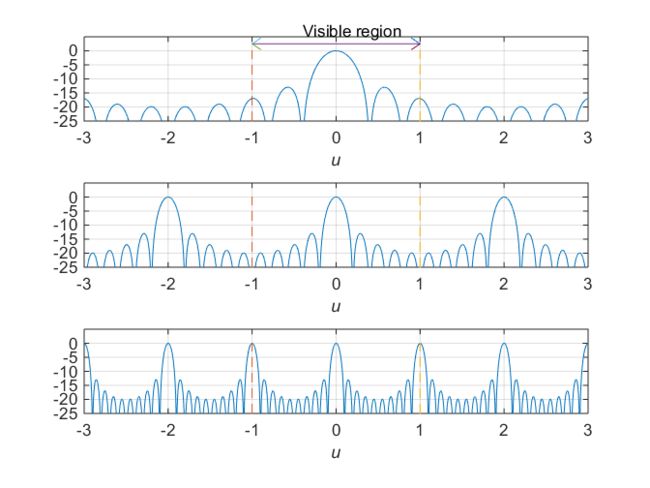
如果阵列的间距大于\(\lambda\)，那么栅瓣的峰值出现在信号传播区域内，即\(\lvert u \rvert \le1\)的区域。此时就会出现峰值响应模糊的问题。另外标准线阵指\(d=\lambda/2\)的均匀线阵。

上面三幅图分别对应着\(d=\lambda/4;d=\lambda/2;d=\lambda\),可以看到当\(d=\lambda\)的时候波束方向图出现了明显的栅瓣。

上面三幅图对应的代码依次如下

clc
% 阵元个数 
N = 11;
psi = (-5 : 1/ 400 : 5) * pi;
beam = zeros(1, length(psi(:)));
y = sin(.5 * psi);
i = find( abs(y) > 1e-12);
j = 1 : length(psi(:));
j(i) = [];
beam(i) = sin((N/2)*psi(i))./(N*y(i));
beam(j) = sign(cos(psi(j) * ((N+1)/2)));

plot(psi / pi, beam);
grid on;
xlabel('{\it \psi}/\pi', 'Fontsize', 9)
ylabel('频率波数响应函数','Fontsize', 9);
axis([-5 5 -0.4 1])

clc;
N = 10;                                % Elements in array
d = 0.5;                               % spacing wrt wavelength
beamwidth = 2/(N*d);                   % null-to-null (LL BW is half this)
D=d*[-(N-1)/2:1:(N-1)/2];              % element locations
u   = [-0.45:0.01:0.45]; 
AS  = exp(-j*2*pi*D'*0);               % BP points to 0
Au  = exp(-j*2*pi*D'*u);
B   = real(AS'*Au)/N;                          % BP

h=plot(u,B,'-');
set(h,'LineWidth',1.5)
hold on
% HPBW
I=find(B>=0.707);
plot([u(min(I)-1) u(max(I)+1)],[B(min(I)-1) B(max(I)+1)],'-')
plot(u(min(I)-1)*[1 1],B(min(I)-1)*[1 1]+0.03*[-1 1],'-')
plot(u(max(I)+1)*[1 1],B(max(I)+1)*[1 1]+0.03*[-1 1],'-')
plot([0.03 0.13],[0.72 0.845],'-')
h=text(0.155,0.84,'D');
set(h,'FontName','Symbol')
text(0.17,0.84,'{\itu}   = HPBW')
h=text(0.185,0.82,'1');
set(h,'Fontsize',10)
text(0.12, 0.7,'0.707')
% BW-NN
plot([-0.2 0.2],[-0.3 -0.3],'-')
plot(-0.2*[1 1],-0.3*[1 1]+0.03*[-1 1],'-')
plot(0.2*[1 1],-0.3*[1 1]+0.03*[-1 1],'-')
h=text(-0.05,-0.35,'D');
set(h,'FontName','Symbol')
text(-0.035,-0.35,'{\itu   = BWNN}')
% h=text(-0.02,-0.37,'2');
% set(h,'Fontsize',10)
% h=text(0.04,-0.37,'\itNN');
% set(h,'Fontsize',10)
% axes
plot([-1 1 ],[0 0],'-')
plot([0 0],[-0 1.1],'-')
% tick marks
plot(-0.4*[1 1],0.03*[-1 1])
plot(-0.2*[1 1],0.03*[-1 1])
plot(0.2*[1 1],0.03*[-1 1])
plot(0.4*[1 1],0.03*[-1 1])
text(-0.005,-0.05,'0')
%tick labels
xx=0.2;
yy=-0.1;
h=text(xx-0.01,yy+0.02,'l');
set(h,'FontName','Symbol')
plot([xx-0.02 xx+0.01],[yy-0.01 yy-0.01],'-')
h=text(xx-0.02,yy-0.05,'\itNd');

xx=-0.18;
yy=-0.1;
h=text(xx-0.01,yy+0.02,'l');
set(h,'FontName','Symbol')
plot([xx-0.02 xx+0.01],[yy-0.01 yy-0.01],'-')
h=text(xx-0.02,yy-0.05,'\itNd');
text(xx-0.04, yy-0.005,'-')

xx=0.41;
yy=-0.1;
h=text(xx-0.01,yy+0.02,'l');
plot([xx-0.02 xx+0.01],[yy-0.01 yy-0.01],'-')
h=text(xx-0.02,yy-0.05,'\itNd');
text(xx-0.035, yy-0.005,'2')

xx=-0.4;
yy=-0.1;
h=text(xx-0.01,yy+0.02,'l');
plot([xx-0.02 xx+0.01],[yy-0.01 yy-0.01],'-')
h=text(xx-0.02,yy-0.05,'\itNd');
text(xx-0.05, yy-0.005,'-2')

text(0.05,1.1,'\itB(u)')
hold off
axis([-0.42 0.42 -0.4 1.2])

%set(gca,'Box','off')
set(gca,'Visible','off')

clc;
N = 10;
n = (-(N-1)/2:(N-1)/2).';
psi = pi * (-3 : 0.001 : 3);
w = 1/N * [ones(N,1)];
d = [1/4 1/2 1];
figure
for k = 1 : length(d)
    vv = exp(1j * 2 * d(k) * n * psi);
    B(k,:) = 20 * log10(abs(w'*vv));
    subplot(3, 1, k);
    plot(psi / pi, B(k, :));
    hold on
    plot([-1 -1],[-25 0],'--');
    plot([1 1],[-25 0],'--');
    axis([-3 3 -25 5])
    set(gca,'YTick',[-25 -20 -15 -10 -5 0])
    grid on
    xlabel('\itu')
    if k == 1
        plot([-1 1],[2.5 2.5])
        plot([-1 -0.9],[2.5 0.5])
        plot([-1 -0.9],[2.5 4.5])
        plot([0.9 1],[0.5 2.5])
        plot([0.9 1],[4.5 2.5])
        text(-0.4,7,'Visible region')
    end
    hold off
end