统计学习笔记—手撕“感知机”

引言

下午拜读了李航老师的《统计学习方法》的感知机部分，随带跑了一个相关算例，于是将所学的知识整理到了这篇博文。不足之处望笔者多加指正。

感知机模型

模型简述

感知机主要的功能就是把一个数据集进行二分类，例如输入人的身高体重，感知机可以判断该人是否肥胖，是机器学习中相对简单的一个模型。开始正文前，我们先约定好符号：

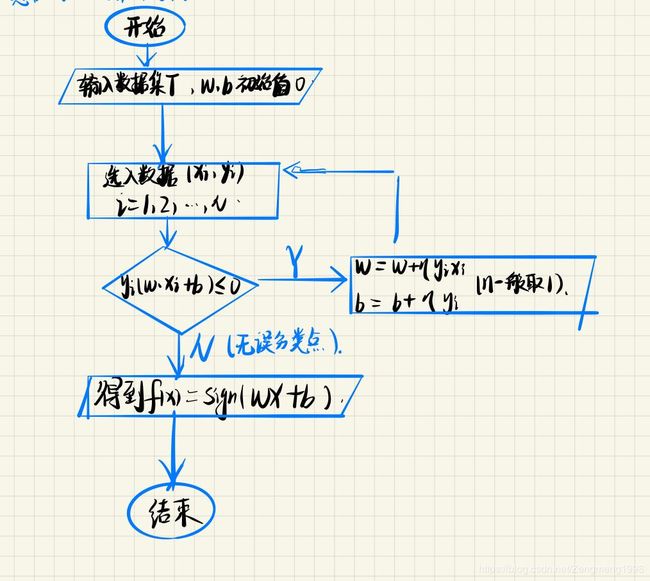
模型的大致实现流程为：

1. 输入一个训练集T；
2. 定义权重向量w、与偏置b；
3. 利用线性分类函数f（x）对数据进行分类；

想要实现这个过程，我们首先需要一个可以完成分类的线性分类函数，那么我们应该怎么定义一个函数帮助我们对数据进行一个正确的分类呢？在此我们又引入了上图所定义的误差函数，如果误差函数（误分类点到分界面的距离*||w||）的和为零，就说明线性分类函数非f（x）将训练集T中的数据的分类全部是正确的。感知机算法做的就是求出误差函数（损失函数）最小时对应的w、b。
本文对算法的推导过程、与算法的迭代次数的数学证明不做详细的叙述，笔者有兴趣的话可自行翻阅原书P42。

感知机算法思想

• 原算法思想：

• 感知机算法的对偶形式：
  

感知机算法性质

1.迭代次数收敛；
2.解（w、b）不唯一，与初始值和训练数据的输入的先后顺序有关；
3.是基于随机梯度下降法的优化算法，策略为对损失函数L（w，b）进行最小化；

算例实现

注：算例的数据集为sklearn库中自带的iris（莺尾花）数据。实现工具为jupyter notebook
笔者利用iris数据集给出的两类莺尾花的花萼长度（sepal length）、花萼宽度（sepal width），通过感知机算法，完成线性分类的函数的建立。

导入数据

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import  matplotlib.pyplot as plt

#莺尾花数据导入
iris=load_iris()
df=pd.DataFrame(iris.data,columns=iris.feature_names)
df['label']=iris.target
df.columns=['sepal length','sepal width','petal length','petal width','label']
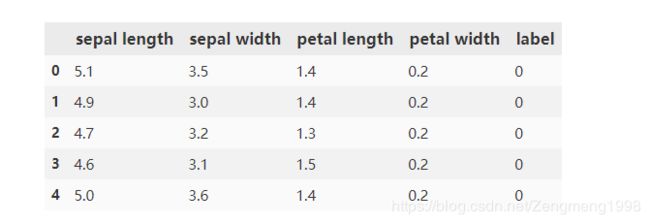
df.head()

实现结果：

使用前两类莺尾花数据

plt.scatter(df[:50]['sepal length'],df[:50]['sepal width'],label='0')
plt.scatter(df[50:100]['sepal length'],df[50:100]['sepal width'],label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal widrth')
plt.legend()

输出：

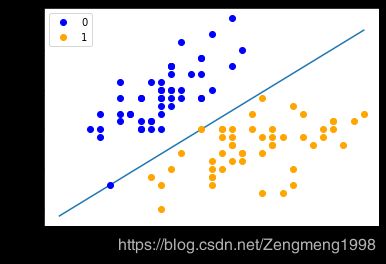
利用感知机进行线性分类

data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])
# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:
    def __init__(self):
        self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data

    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y

    # 随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate * np.dot(y, X)
                    self.b = self.b + self.l_rate * y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

    def score(self):
        pass

perceptron = Model()
perceptron.fit(X, y)
x_points = np.linspace(4, 7, 10)
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

输出：

小结

对于机器学习算法的学习，笔者尝试的是啃书＋复现，但是深感其中数学的深奥，将源码理解是容易的，数学入门也算简单，但是对于其背后支撑算法的数学证明、数学定义笔者仍未能吃透，上述不足之处，望多多指正。

参考

https://github.com/wzyonggege/statistical-learning-method
李航 《统计学习方法》（第二版）P36-47

轻松一刻

考研男：做我女朋友好不好？
考研女：e^x在无穷大处的极限是多少你知道么？知道我就接受你；
考研男：简单！0或正无穷；
考研女：对不起我拒绝你的表白，因为极限具有唯一性，而你不具有……