树上差分详解

树上差分

Max Flow NKOJ3605

给定一棵有N个点的树，所有节点的权值初始时都为0。
有K次操作，每次指定两个点s,t，将s到t路径上所有点的权值都+1。
请输出K次操作完毕后权值最大的那个点的权值。 2≤N≤50,000 1≤K≤100,000

对于每一次修改s,t，将s,t的权+1;将LCA(s,t)和father[LCA(s,t)]的权-1;一个点最终被覆盖的次数就是这个点所在子树的权和。

对于每一次修改s,t，将s,t的权+1;将LCA(s,t)和father[LCA(s,t)]的权-1;一个点最终被覆盖的次数就是这个点所在子树的权和。

         数据结构题中解法千变万化，但分析最近几年的趋势来看，有一种比较重要的思想->树上差分。（会树剖的大神不要嘲笑，虽然很多时候树剖都能很好解决QwQ）。至少，树上差分熟练的话还是可以解决很多问题的。这里就先分析两种基本的差分思路。

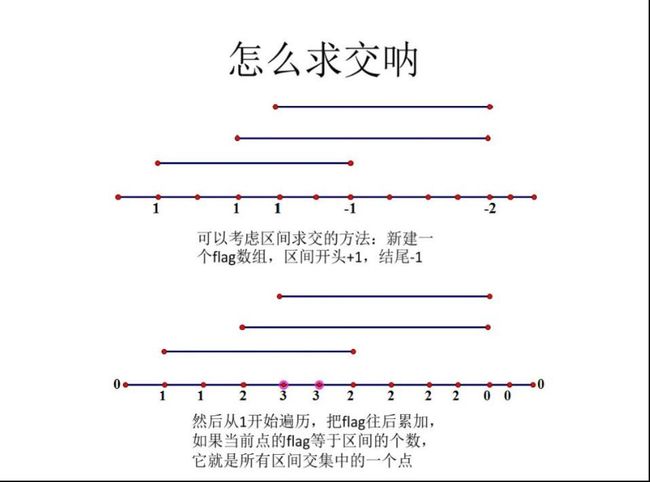
1.找被所有路径共同覆盖的边。

         可能这样讲不是很详细，那就看一道例题【Noip2015】运输计划（【Bzoj4326】）。大意是有许多条运输路径，让你在把一条边的用时不计的情况下找到最大路径的最短用时。看到这题很明显想到二分答案，而对于每一个答案，我们要记录超过此答案的计划。之后我们该怎么办呢，如果有一条边被所有计划共同覆盖，且去掉它（用时降为0）后能使得其中超答案时间最多的边都不超时，那便是可行答案。而我们就要来分析一下如何找这条边。

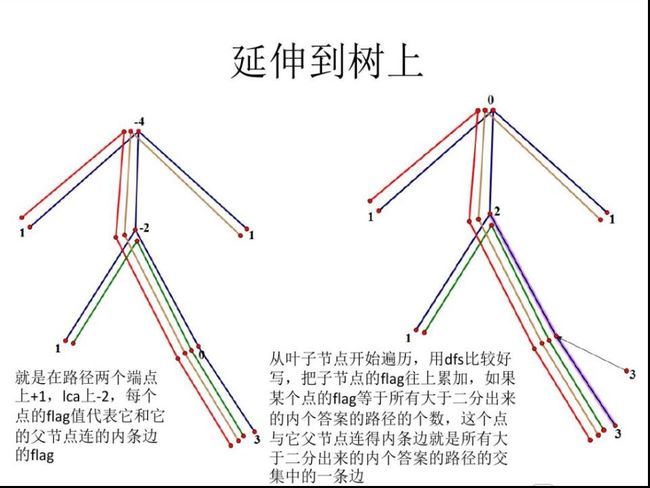
   首先我们除了一般的grand，depth等数组以外，多开两个数组：tmp和prev。tmp用来记录点的出现次数（具体点说实际上记录的是点到其父亲的边的出现次数），prev记录每个点到其父亲的那条边（这里根据题目记的权值，有必要时也可以记编号）。对于一条起点s，终点t的路径。我们这样处理：tmp[s]++,tmp[t]++,tmp[LCA(s,t)]-=2。（记住：最后要从所有叶结点把权值向上累加。）以一次操作为例，我们来看看效果（可以画一张图）。首先tmp[s]++，一直推上去到根，这时候s到root的路径访问次数都+1，tmp[t]++后，t到lca路径加了1，s到lca路径加了1，而lca到根的路径加了2。这时，我们只需要tmp[LCA(s,t)]-=2，推到根，就能把那些多余的路径减掉，达到想要的目的。而这是一次操作，对于很多次操作的话，我们只需要维护tmp，而不必每次更新到根，维护好tmp最后Dfs一遍即可。这时如果tmp[i]==次数的话，说明i到其父亲的边是被所有路径覆盖的。

         光是看起来可能很麻烦，建议画一张图模拟一个简单的过程。代码实现的话可以参考这个运输计划中的二分check过程…丢上来。（如果像这样多次找的话注意tmp的重置。）（kth可以暂时不用管，这只是这道题中维护的点的编号。）

bool check(int x){
    int cnt=0,dist=0;
    memset(tmp,0,sizeof(tmp));
    for(int i=1;i<=m;i++){
        if(Q[i].Dis > x){
            tmp[Q[i].s]++;tmp[Q[i].t]++;
            tmp[Q[i].lca] -= 2;
            dist=chkmax(dist,Q[i].Dis-x);
            cnt++;
        }
    }
    if(!cnt) return true;
    for(int i=n;i>1;i–)
        tmp[grand[kth[i]][0]] += tmp[kth[i]];
    for(int i=2;i<=n;i++)
        if(tmp[i]==cnt && prev[i]>=dist)
            return true;
    return false;
}

bool check(int x){  
    int cnt=0,dist=0;  
    memset(tmp,0,sizeof(tmp));  
    for(int i=1;i<=m;i++){  
        if(Q[i].Dis > x){  
            tmp[Q[i].s]++;tmp[Q[i].t]++;  
            tmp[Q[i].lca] -= 2;  
            dist=chkmax(dist,Q[i].Dis-x);  
            cnt++;  
        }  
    }  
    if(!cnt) return true;  
    for(int i=n;i>1;i--)   
        tmp[grand[kth[i]][0]] += tmp[kth[i]];  
    for(int i=2;i<=n;i++)  
        if(tmp[i]==cnt && prev[i]>=dist)  
            return true;  
    return false;  
}  

2.将路径上的所有点权值加一，求最后点的权值。

           乍一看和上一个操作是差不多的，但实际上还是有一些不同，如果自己在画图中发现问题就能体会到这种差异。

        而对于这种操作，我们该怎么实现呢？首先还是通过例题了解具体操作，这里推荐【JLOI2014】松鼠的新家（【Bzoj3631】）大意是有一些路径，每次经过时要将路径上的所有点权值加上1。对于这种操作，我们仍需要一个tmp数组。这里的tmp记录的就是点被访问的次数（也可以说是累加的权值）。这个操作的具体实现和上一个思想类似（都是差分）实现的话也只有少许不同。此操作中我们这样维护：每次经过一条边，（如从u到v）我们让tmp[u]++,tmp[v]++,tmp[LCA(u,v)]–,tmp[grand[LCA(u,v)][0]]–。（最后要把tmp推上去）以一次添加为例想象一下，首先u到根的路径上tmp都+1，此时u到根间结点tmp都为1，之后v到根路径上tmp+1，此时u到LCA前一个，v到LCA前一个点的tmp都+1，而LCA到根的所有点都+2，然后从tmp[LCA]–,更新上去，此时u-v路上所有tmp都+1，已经达到目的。而多余的是什么部分呢，也就是LCA的上一个结点（grand[LCA][0]）到根的这一段都多加了1，所以tmp[grand[LCA][0]]–,更新上去，也就完成了。实际操作时也不需要每次更新都推上去，只要把四个tmp维护好，最后Dfs走一边就更新完了。

如果理解不了的话建议还是画一张图（…可以理解的…吧…？）反正体会其中的思想，自己多模拟过程。（这个

…）不知道是不是表达能力的问题（自以为还是表达清楚了的）…实在看不懂的话…我也很难过啊。

代码也扔一个（一小段）

void pushdown(int x)
{
    for(int i=head[x];i;i=next[i])
    {
        if (to[i]==grand[x][0]) continue;
        pushdown(to[i]);
        tmp[x]+=tmp[to[i]];
    }
}

int main(){
    n = read();
    for(int i=1;i<=n;i++)
        a[i] = read();
    for(int i=1;i
        x = read();y = read();
        Add(x,y);Add(y,x);
    }
    Dfs(a[1]);
    for(int i=1;i
        int u = a[i],v = a[i+1];
        tmp[u]++;tmp[v]++;
        tmp[Lca(u,v)]–;
        tmp[grand[Lca(u,v)][0]]–;
    }
    pushdown(a[1]);
    for(int i=2;i<=n;i++)
        tmp[a[i]]–;
    for(int i=1;i<=n;i++)
        printf(”%d\n”,tmp[i]);
    return 0;
}

void pushdown(int x)  
{  
    for(int i=head[x];i;i=next[i])  
    {  
        if (to[i]==grand[x][0]) continue;  
        pushdown(to[i]);  
        tmp[x]+=tmp[to[i]];  
    }  
}  

int main(){  
    n = read();  
    for(int i=1;i<=n;i++)  
        a[i] = read();  
    for(int i=1;i

反正注意两种操作的相同与不同之处，可以多刷一些题加深理解，这篇文也许（hhh也许）还会更新，如果

有新的差分思路或者好题啥的，还会update的。

看不懂的话可以加qq骚扰我辣，虽然加了也不一定讲得清…反正反正反正qwq…要知道我讲得这么不清楚是

爱得深沉的表现知道吗？？！

hhhhhhhhhhhhhh又精神分裂了，反正记住是因为想讲清（导致讲得不清…？）hhhhh。就这样，讲得烂不

要喷我，不接受。hhhhhhh。

感谢两位dalao的博客：
1.http://blog.csdn.net/yao166164474/article/details/52673333
2.http://blog.csdn.net/zhayan9qvq/article/details/54999472?readlog