深层神经网络(DNN)的一些基本概念

本文介绍一些DNN的概念，包括激活函数、损失函数、优化算法等
声明：本文的主要内容及代码主要来源于实战Google深度学习框架

1 激活函数

DNN的最大突破就是引入了非线性激活函数，如果没有激活函数，那么无论神经网络深度如何，它与一个1层网络本质上是没有区别的。通过增加网络的层数，并且在层与层之间添加非线性项以及偏置项$f(\sum _i{x}_i{w}_i+b)$能够很好增加DNN的拟合性能。
常用的激活函数列在下方

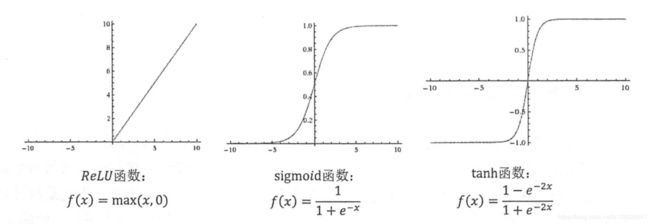
目前TensorFlow提供了7种不同的非线性激活函数，常用的是tf.nn.relu()、tf.sigmoid()、tf.tanh()，下方代码实现了配合激活函数的前向传播算法

a = tf.nn.relu(tf.matmul(x,w1) + biases1)

2 损失函数

监督学习主要分为分类问题和回归问题，两个问题分别有各自对应的损失函数。针对特定问题，还可以自定义损失函数。

2.1 分类问题

分类问题的损失函数主要用交叉熵(cross entropy)损失函数，对于二分类问题其定义为

$$loss=-(y\ast (log\hat{y})+(1-y)\ast log(1-\hat{y}))$$

其中$\hat{y}$定义为模型预测值，y定义为样本真实值
对于多分类问题，其定义为

注意到在多分类问题中，为了将模型的多个输出进行归一化，需要将输出进行softmax回归，定义为：

$$softmax({\hat{y}}_i)=\frac{e^{{\hat{y}}_i}}{{\sum }_{i=1}^n{e}^{{\hat{y}}_i}}$$

其中${\hat{y}}_i$定义为某一个类别的输出。
这样的话，多分类的损失函数也可以定义为

$$loss=\sum _{i=1}^n{y}_i\ast (log{\hat{y}}_i)$$

因为softmax一般会与cross entropy一起使用，所以TensorFlow里边对它们进行了封装，可以直接用以下代码获得模型输出值y和真实值y_的cross entropy：

cross_entropy = tf.nn.softmax_entropy_with_logits(y,y_)

2.2 回归问题

回归问题与分类问题不同之处在于回归问题预测的是一个数值，而不是一个类别，因此其损失函数可以定义为均方误差：

$$MSE(y,y^{\prime })=\frac{{\sum }_{i=1}^n(y_i-y_i^{\prime }{)}^2}{n}$$

在TensorFlow中实现也很简单：

mse = tf.reduce_mean(tf.square(y,y_))

2.3 自定义损失函数

TensorFlow中还支持自定义损失函数，举例在回归问题中，如果模型预测值大于真实值的损失量与小于真实值的损失量不一致，那损失函数可以用下列公式定义：
$$Loss(y,y^{\prime })=\sum _{i=1}^{n}f(y_i,y_i^{\prime })$$

$$f(x,y)\{\begin{array}{c}a(x-y)x\le y\\ b(y-x)y>x\end{array}$$
在TensorFlow中可以用以下代码实现这个公式：

loss = tf.reduce_sum(tf.select(tf.greater(x,y), a*(x-y), b*(y-x)))

3 优化算法

有多种数值方法可以用于计算函数的极小值，最简单的是梯度下降法：
$$x_{n+1}=x_n-\eta \frac{\partial y}{\partial x_n}$$
注意此法的损失函数y是在所有训练数据的损失的均值，如果训练数据太大，那么对其求损失的计算代价会很高，因此一般采用的是随机梯度下降法（SGD），计算的损失是一条训练数据或者多条训练数据的均值。只要数据是独立同分布的，随机梯度下降法能够更快地获得损失函数的极小值。

除此之外，还有多种方法可以用于获得损失函数极小值，如带Momentum的梯度下降法，RMSprop等等。在TensorFlow中都能够调用：

tf.train.GradientDescentOptimizer#随机梯度下降
tf.train.AdamOptimizer#Adam法
tf.train.MomentumOptimizer#带动量的随机梯度下降

4 学习率的设置

在优化损失函数的时候，需要设置学习率(learning rate)来确定参数变化的速度。如果学习率设置过大，参数变化过快，损失函数有可能会一直在极小值附近摆动不能收敛。如果学习率设置过小，则损失函数会收敛过慢。
因为在刚开始训练时，参数设置是随机的，所以其距离极小值肯定比较远，所以此时可以把学习率设置得稍大。训练一段时间后再把学习率逐渐变小，使损失函数更接近极小值。
在TensorFlow中利用tf.train.exponential_decay()可以设置指数衰减的学习率，使学习率在经过一定学习次数后逐渐变小。以下代码示范如何使用。

train_step = 100
global_step = tf.Variable(0)
x = tf.Variable(tf.constant(5,dtype=tf.float32,name='x'))
y = tf.square(x)
learn_rate = tf.train.exponential_decay(0.1,global_step,1,0.96,staircase=False)
train_op = tf.train.GradientDescentOptimizer(learn_rate).minimize(y,global_step=global_step)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(train_step):
        sess.run(train_op)
        x_val = sess.run(x)
        learning_rate = sess.run(learn_rate)
        if i%10==0:
            print("i = %d, x = %f., learning_rate = %f." %
            (i,x_val,learning_rate))

代码目标是优化$y=x^2$, x初始化为5，训练次数为100。learn_rate用tf.train.exponential_decay定义，初始化为0.1，每训练一次学习率都乘以0.96。
代码中，global_step指的是当前学习次数。

5 正则化

在训练过程中，在很多情况下神经网络会尽量模拟训练数据的行为，创建一个能够将训练数据完美分割开的模型。但是实际中我们的目的是要使模型在没有见过的数据上能够用良好的性能。在训练数据上表现太完美的模型在未知数据上并不一定表现好，这个就是训练中的过拟合情况。
为了避免过拟合行为，可以在损失函数中加入正则化项，当模型过于复杂时，正则化项会增加，从而增大损失函数。因此添加正则化后的模型能够在拟合训练数据与增加模型复杂度之间保持平衡。
常用的正则化项有L1正则化和L2正则化，分别定义为：
$$L1:R(w)=||w|{|}_1=\sum _i|w_i|$$
$$L2:R(w)=||w_2|{|}^2=\sum _i|w_i^2|$$

两种正则化的方法都是通过限制权重中数值的大小来限制模型复杂度。很明显如果权重中数值过大，训练数据中的微小扰动就可能导致输出结果的变化。
L1正则化会使参数变得稀疏，也就是使参数中0元素的元素增多，其不可导。
L2正则化会使参数趋近于0，其可导。在对损失函数优化时，需要对函数求导数，因此包含L2正则化的损失函数优化起来会更方便。
以下代码给出了用TensorFlow的集合来优化一个包含5层带L2正则化的损失函数的方法

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

dataset_size = 200
data = []
label = []
np.random.seed(0)

# 以原点为圆心，半径为1的圆把散点划分成红蓝两部分，并加入随机噪音。
for i in range(dataset_size):
    x1 = np.random.uniform(-1,1)
    x2 = np.random.uniform(0,2)
    if x1**2 + x2**2 <= 1:
        data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
        label.append(0)
    else:
        data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
        label.append(1)
        
data = np.hstack(data).reshape(-1,2)
label = np.hstack(label).reshape(-1, 1)
plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()

#定义一个生成权重并将L2正则化项加入到losses集合中
def get_weight(shape,var_lambda):
    #生成权重
    var = tf.Variable(tf.random_normal(shape),dtype=tf.float32)
    tf.add_to_collection('losses',tf.contrib.layers,l2_regularizer(var_lambea)(var))
    return var


#构建神经网络 
x = tf.placeholder(tf.float32,shape=[None,2])
y_ = tf.placeholder(tf.float32,shape=[None,1])

layer_dimension = [2,10,5,3,1]#每层神经网络节点数
n_layer = len(layer_dimension)#网络层数

cur_layer = x
in_dimension = layer_dimension[0]

#循环生成神经网络，一共四个隐藏层，每层的维度分别为输入x[1,2],w1[2,10],w2[10,5],w3[5,3],w4[3,1],输出y[1]
for i in range(1,n_layer):
    out_dimension = layer_dimension[i]
    w = get_weight([in_dimension,out_dimension],0.001)#生成每层权重，并将权重的L2正则化加入的损失函数集合中
    bias = tf.Variable(tf.constant(0.1,shape=[out_dimension]))#生成偏置项
    cur_layer = tf.nn.relu(tf.matmul(cur_layer,w)+bias)#使用relu激活函数生成下一个输出
    in_dimension=layer_dimension[i]
    
y = cur_layer
#定义均方损失函数和带正则化的损失函数
mse_loss = tf.reduce_mean(tf.square(y-y_))
tf.add_to_collection('losses',mse_loss)
loss = tf.add_n(tf.get_collection('losses'))

#利用Adam方法进行优化
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
train_step = 1000

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    #tf.global_variables_initializer().run()
    for i in range(train_step):
        sess.run(train_op,feed_dict={x:data,y_:label})
        if i%100==0:
            print("i = %d,loss = %f." %(i,sess.run(mse_loss,feed_dict={x:data,y_:label})))

总结

本文讲述了一些DNN的基本概念以及在TensorFlow中的基本应用。包括了激活函数的种类，损失函数的定义，优化算法的类别，学习率的定义以及正则化。
DNN的内容繁多，本文并不能囊括全部，将来有时间会另开一篇文章讲述本人了解过的内容。