摘要:之前对ceph的crush算法的理解,很多时候没有针对问题来考虑。我现在就提出几个问题
1,ceph怎么做到的每次down掉一个osd或者新增一个osd后,只有少量的数据迁移?而不是所有数据都在osd之间来回迁移?(据说sheepdog是大量迁移,所以这个就别拿来和ceph比性能了,连弹性扩容都做不到。)
2,一块数据A写入pg1(osd1),现在新增osd了,导致pg1迁移到osd2上,那么下次需要读数据A,还能找到数据位置吗?
3,一个oid映射到pgid,是怎么哈希映射的?一个文件名真的可以哈希后得到文件夹的名字?真像网上说的那样,是文件名哈希后,用哈希值value除以文件夹总数取余数(oid%pg_num) ?
一,怎么把一个文件名映射到文件夹?(也就是object怎么映射到pg)
假如我有1个文件,需要哈希映射到1000个文件夹。 拿ceph来说,就是1个object怎么映射到1000个pg。
网上的说法:
1,hash(object) 得到一个哈希值 value 。
2,用这个value除以10000,取余数。
这样的做法确实也可以让object随机映射到1000个pg中的一个。但是只是知道了1000个pg的第几个pg,还要根据算出的序号,去1000个pg中查询出pgid。这样做效率是不行的。ceph一贯履行不需查找,算算就好的承诺。
ceph的做法:
1,每次创建一个pool的时候让pg的id变得连续。如果16个pg,那pgid就从0~f 。如果1024个pg,那么pdid就从0~3ff。
下图中0.3ff 前面的0 表示 poolid。
 0。
0。
2,通过object取得的哈希值value &mask运算,得出pgid的值。
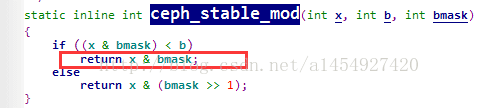
mask为pg数量-1,因为pgid是从0开始的,所以需要-1
这样无论怎么计算pgid始终为0~mask之间。也就是pg总数里的任意一个值。这样object会被均匀的分配到任意一个pg
二,crush算法怎么做到每次有osd新增和删除,只有少量的pg产生迁移,而不是所有的pg在osd之间重新定位?
1,一个pg请求的定位,会选择一个机房,然后在机房里选择一个机架,机架上选择一个服务器,服务器上选择一个osd。完成pgid-->osdid的映射。
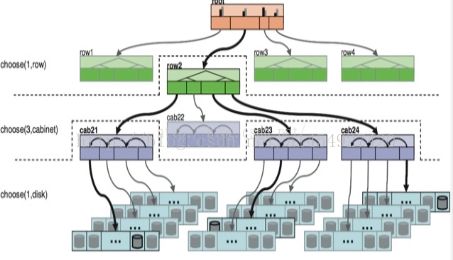
2, 以上的机房,机架,服务器,osd。我们都可以认为是一个item。那怎么在10个item中选择一个,是通过哈希值处于10取余数的方式吗?
当然不是,如果这样做。就会导致新增,删除osd,集群里的所有pg都需要迁移。因为新增osd后,哈希的范围变了,ceph集群里所有的pg都需要重新哈希选择位置。
3,ceph提供了多种选择一个item的算法,这些算法统称bucket算法。下面比较多种bucket算法对于osd变动,造成的数据迁移量。
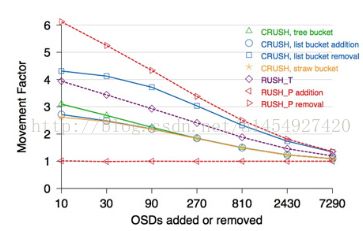
横轴代表osd新增和删除的数量,纵轴代表pg发生的迁移率。可以发现RUSH_P在新增和删除上呈现2个极端,新增osd的时候pg迁移率很小。
而删除osd的时候迁移率很大,我们平常默认使用的straw是比较这种的方案。为图中的黄色线条。也就是说pg的迁移率和bucket算法有关。
4,那bucket算法为什么在新增删除osd的时候呈现少量的迁移率?下面我们把crush straw算法的代码提取出来测试研究。
| #include
#include
#include
using namespace std;
typedef unsigned int __u32;
#define crush_hash_seed 1315423911 #define crush_hashmix(a, b, c) do { \
a = a - b; a = a - c; a = a ^ (c >> 13); \
b = b - c; b = b - a; b = b ^ (a << 8); \
c = c - a; c = c - b; c = c ^ (b >> 13); \
a = a - b; a = a - c; a = a ^ (c >> 12); \
b = b - c; b = b - a; b = b ^ (a << 16); \
c = c - a; c = c - b; c = c ^ (b >> 5); \
a = a - b; a = a - c; a = a ^ (c >> 3); \
b = b - c; b = b - a; b = b ^ (a << 10); \
c = c - a; c = c - b; c = c ^ (b >> 15); \
} while (0)
//crush straw算法,参数1为pgid,参数2为一组item,参数3为副本数
static __u32 crush_hash32_rjenkins1_3(__u32 a, __u32 b, __u32 c)
{
__u32 hash = crush_hash_seed ^ a ^ b ^ c;
__u32 x = 231232;
__u32 y = 1232;
crush_hashmix(a, b, hash);
crush_hashmix(c, x, hash);
crush_hashmix(y, a, hash);
crush_hashmix(b, x, hash);
crush_hashmix(y, c, hash);
return hash;
}
int main() //对straw算法进行测试
{
int testpgid[1000];
srand((unsigned)time(NULL));
for (int i = 0; i < 1000; i++) //选取1000个pg进行测试,pgid取一个随机数
{
testpgid[i] = rand();
}
//int testpgid[10] = {432879,32189,8879,3871,1048390,73167,46104,32169,34791,31280};
for (int n = 0; n < 1000; n++) //对1000个pg进行1000次item选举测试
{
int i;
unsigned int weight = 1;
int item[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; //针对10个item来模拟
int high = 0;
unsigned long long high_draw = 0;
unsigned long long draw;
int result;
for (i = 0; i <10; i++)
{
draw = crush_hash32_rjenkins1_3(testpgid[n], item[i], 3);
draw &= 0xffff;
draw *= weight;
if (i == 0 || draw > high_draw) {
high = i;
high_draw = draw;
}
}
result = high;//result为最终在10个item中选出的item号 int j;
int item_del[9] = { 1, 2, 3, 4, 5, 6, 8, 9, 10 }; //模拟删掉一个item 7
int high1 = 0;
unsigned long long high_draw1 = 0;
unsigned long long draw1;
int result1;
for (j = 0; j <9; j++)
{
draw1 = crush_hash32_rjenkins1_3(testpgid[n], item_del[j], 3);
draw1 &= 0xffff;
draw1 *= weight;
if (j == 0 || draw1 > high_draw1) {
high1 = j;
high_draw1 = draw1;
}
}
result1 = high1;//result1为最终在9个item中选出的item号 int k;
int item_add[11] = { 1, 2, 3, 4, 5, 6, 7,8, 9, 10,11 }; //模拟新增一个item11
int high2 = 0;
unsigned long long high_draw2 = 0;
unsigned long long draw2;
int result2;
for (k = 0; k <11; k++)
{
draw2 = crush_hash32_rjenkins1_3(testpgid[n], item_add[k], 3);
draw2 &= 0xffff;
draw2 *= weight;
if (k == 0 || draw2 > high_draw2) {
high2 = k;
high_draw2 = draw2;
}
}
result2 = high2;//result2为最终在11个item中选出的item号
cout << testpgid[n] << " " << result << " " << result1 << " "<< result2<< endl;
} //打印的内容为:pgid号,没有osd变动时候选出的item, 删除一个osd后选出的item, 新增一个osd后选出的item
return 0;
} |
对1000个pg进行测试,每个pg在10个item里选一个,先后删除一个item,新增一个item测试。测试结果发现,不管是新增还是删除item。
straw算法对某个item的选择一直在坚持,只有少数时候会由于新增和删除item产生变化,大部分时候不管删除还是新增item,都坚持选择原来的item。
下面为测试结果。
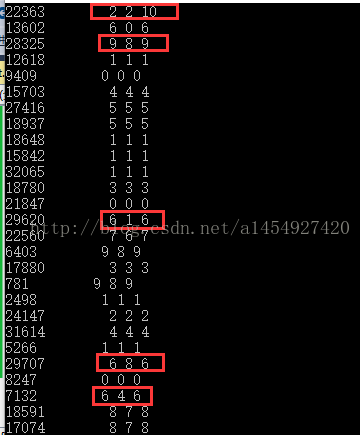
可以看到大部分时候,不管新增删除osd,straw算法都是坚持原来的选择,只有少数时候会改变。
所以这就决定了。新增osd的时候,只有一小部分的pg需要重新定位。迁移位置。
5, 我们通过算法的原理来分析下原因。straw算法如下:
static __u32 crush_hash32_rjenkins1_3(__u32 a, __u32 b, __u32 c)
从10个item里选取一个哈希值最大item的作为入选的item。
如果你新增一个item,影响10个item中最大值的那个可能性并不大。
你是班里最高的,班里来了一个新同学,新同学比你高的可能性并不大。绝大部分可能你还是最高的。
删除一个item也是同样的道理。




