python学习笔记第八章(体育竞技分析)
我们在这个实例中,我们需要根据对两个人A、B的能力值来预测两人的胜率各是多少。
我们假定以下比赛规则:
双人击球比赛:
1、A、B两个人,回合制的五局三胜。
2、开始时一方先发球,直至判分,接下去胜者发球。
3、球员只能在发球局得分,15分胜一局。
我们处理一个问题时的两种思路有自顶而下和自底而上:
自顶向下:(执行)
将一个很大的问题表述为许许多多个小问题的组合,然后利用相同的方法来分解小问题,直到小问题可以简单解决。
自底向上:(设计)
分单元去测试,逐步组装,即按自顶向下的相反路径去操作,直到系统每一部分以组装的思路都经过测试与验证。
在这道题中,我们先分析题目的步骤:
步骤:
1、将最基本的介绍性信息打出
2、获得参数
3、通过得到A和B两人的各项能力值来模拟n局比赛
4、输出球员模拟的比赛获胜情况,并算出概率
1、将最基本的介绍性信息打出
def printintro():
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1间的小数来表示")
这部分代码比较简单,是为了让人更容易理解输入的部分。
2、获得参数
def getinputs():
a=eval(input("请输入选手A的能力值(0—1):"))
b=eval(input("请输入选手B的能力值(0—1):"))
n=eval(input("模拟比赛场次:"))
return a,b,n
利用输入函数很容易的完成这部分的代码编写。
4、输出球员模拟的比赛获胜情况,并算出概率(先跳过第三步)
def printsummary(winsA,winsB):
n=winsA+winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场,占比{:0.1%}".format(winsA,winsA/n))
print("选手B获胜{}场,占比{:0.1%}".format(winsB,winsB/n))
这部分即为模拟多次比赛,然后胜场除以总场数(模拟次数)即为预测的胜率。
3、通过得到A和B两人的各项能力值来模拟n局比赛
模拟N据比赛可以看作N次模拟一局比赛。这里我们定义一个每一次模拟的函数sim1game(probA,probB),然后编写N次模拟的代码。
def simngames(n,probA,probB):
winsA,winsB=0,0
for i in range(n):
scoreA,scoreB=sim1game(probA,probB)
if scoreA>scoreB:
winsA+=1
else:
winsB+=1
return winsA,winsB
这段代码为完成一个很简单的对比,输出谁嬴谁输,然后做一个统计的功能。
5、sim1game()函数编写
我们认为当到gameover的时候竞技结束。
def sim1game(probA,probB):
scoreA,scoreB=0,0
serving='A'
while not gameover(scoreA,scoreB):
if serving=="A":
if random()这里我们需要使用random库来产生一个0-1的随机数,若随机数大于能力值,则判输并且换人发球,小于能力值,则判赢。
6、gameover(a,b)函数的编写
def gameover(a,b):
return a==15 or b==15
代码比较容易。
完整代码如下:
#体育竞技分析
from random import random
def printintro():
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1间的小数来表示")
def getinputs():
a=eval(input("请输入选手A的能力值(0—1):"))
b=eval(input("请输入选手B的能力值(0—1):"))
n=eval(input("模拟比赛场次:"))
return a,b,n
def printsummary(winsA,winsB):
n=winsA+winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场,占比{:0.1%}".format(winsA,winsA/n))
print("选手B获胜{}场,占比{:0.1%}".format(winsB,winsB/n))
def gameover(a,b):
return a==15 or b==15
def sim1game(probA,probB):
scoreA,scoreB=0,0
serving='A'
while not gameover(scoreA,scoreB):
if serving=="A":
if random()scoreB:
winsA+=1
else:
winsB+=1
return winsA,winsB
def main():
printintro()
proA,proB,n=getinputs()
winsA,winsB=simngames(n,proA,proB)
printsummary(winsA,winsB)
main()
结果如下:
1、第一组数据:A:0.45、B:0.5

2、第二组数据:A:0.49、B:0.5
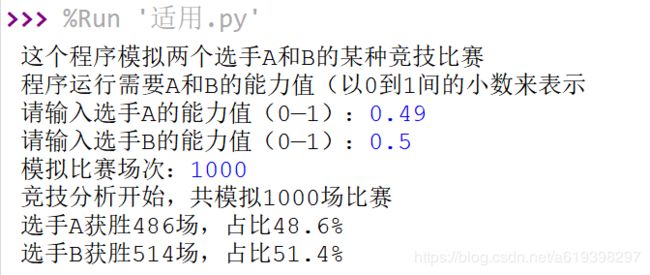
3、第三组数据:A:0.45、B:0.55
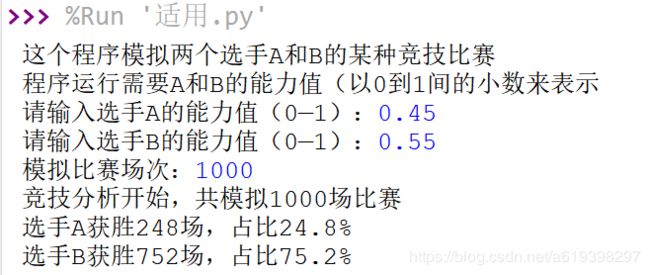
从以上的结果我们可以得到一些结论,比如,能力值只相差0.05,但胜率会高出40%左右,所以从数值上我们可以得出如果一场比赛十分胶着,那么两个人的实力会几乎相同,能力值会十分接近。
以上为我学习的python课程中的原本代码,但我自己思考后认为,如果每次从A开始发球,我们有一定的不公平,所以我希望能够在模拟中让A、B轮流发球,如此可能对竞赛的公平性有更大的提升。
我的改进如下:
def simngames(n,probA,probB):
winsA,winsB=0,0
for i in range(n):
if i%2==0:
scoreA,scoreB=sim1game(probA,probB)
else:
scoreA,scoreB=sim2game(probA,probB)
if scoreA>scoreB:
winsA+=1
else:
winsB+=1
return winsA,winsB
在改进代码的部分,主要添加了,若第n次时,n时二的倍数,则换B来发球。
加入一个sim2game()函数:
def sim2game(probA,probB):
scoreA,scoreB=0,0
serving='B'
while not gameover(scoreA,scoreB):
if serving=="A":
if random()完整代码如下:
#体育竞技分析
from random import random
def printintro():
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1间的小数来表示")
def getinputs():
a=eval(input("请输入选手A的能力值(0—1):"))
b=eval(input("请输入选手B的能力值(0—1):"))
n=eval(input("模拟比赛场次:"))
return a,b,n
def printsummary(winsA,winsB):
n=winsA+winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场,占比{:0.1%}".format(winsA,winsA/n))
print("选手B获胜{}场,占比{:0.1%}".format(winsB,winsB/n))
def gameover(a,b):
return a==15 or b==15
def sim1game(probA,probB):
scoreA,scoreB=0,0
serving='A'
while not gameover(scoreA,scoreB):
if serving=="A":
if random()scoreB:
winsA+=1
else:
winsB+=1
return winsA,winsB
def main():
printintro()
proA,proB,n=getinputs()
winsA,winsB=simngames(n,proA,proB)
printsummary(winsA,winsB)
main()
仍然运行以上三组数据,多运行两次,得到以下结果:
1、第一组数据:A:0.45、B:0.5
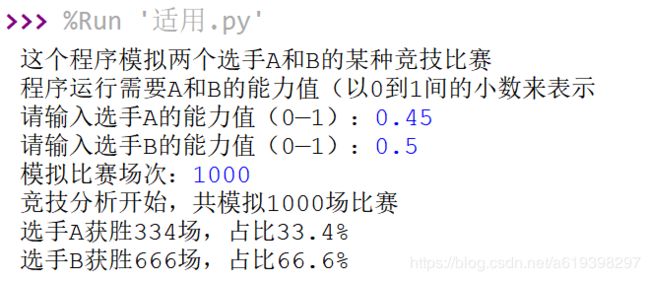
2、第一组数据:A:0.49、B:0.5

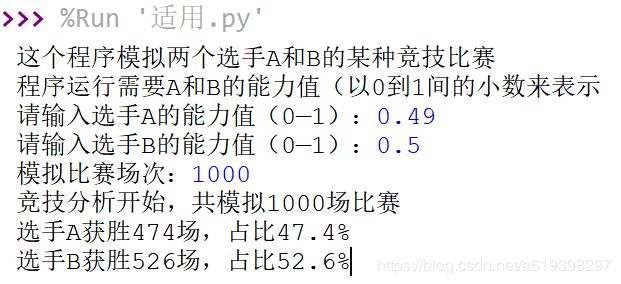

此,我们再进行分析,发现在差距大的情况下,差距更多的是变大了,而差距小的情况会更多变一些,会更接近了,我认为这是更加公平的体现。
在有一定差距的情况下,差距的可视化更强,更能体现出差距的存在,但若是差距很小的情况下,甚至会出现能力值低的人胜率更高的情况。
从直观的意义上来理解,若是两人差距很大,则在第一场自己发球输掉比赛只会让球权转移,但若是对手发球,则输掉会使对手直接得分;但是差距小的情况下,两人保住球权和丢掉球权的概率几乎一致,所以两人的胜率会十分接近。
