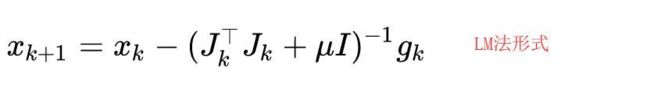【优化算法】基于Python语言的梯度下降法、牛顿法、LM法
梯度下降法
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了
算法步骤:
利用梯度下降的方法求解步骤如下:
![]()
1、求梯度
2、向梯度相反的方向移动 ,其中, alpha为步长。如果步长足够小,则可以保证每一次迭代都在减小,但可能导致收敛太慢,如果步长太大,则不能保证每一次迭代都减少,也不能保证收敛。
3、循环迭代步骤2,直到 l两次函数的值的差值足够小,比如0.00000001,也就是说,直到两次迭代计算出来的值基本相同,则说明此时函数值已经达到局部最小值了。
4、此时,输出X ,这个就是使得函数最小时的取值
迭代公式: x- a* df
代码实现:
import math
#得到原函数和一阶导数
def f(x):
return x**2-4*math.sin(x)
def df(x):
return 2*x-4* math.cos(x)
def gradient(df,x0):
xn = float(x0)
loop = 1
a = 0.01
while 1:
print ('迭代次数为:',str(loop))
xm = df(xn)
print ('old x:'+str(xn))
q = a * xm
xn = xn-q #迭代
e_tmp = abs(0-df(xn))
if e_tmp < 0.00001:
break
print( 'new x:'+str(xn))
loop=loop+1
return xn
x = gradient(df,3)
y = f(x)
print ('极值点为: '+str(x))
print('极小值为:'+str(y))
牛顿法
牛顿迭代法(Newton’s method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
代码实现:
import math
# df一阶导数 ddf二阶导数
def newtons(df,ddf,x0):
xn = float(x0)
loop = 1
while 1:
print ('迭代次数为:',str(loop))
k = ddf(xn)
xm = df(xn)
print ('old x:'+str(xn))
q = xm/k
xn = xn-q #迭代
e_tmp = abs(0-df(xn))
if e_tmp < 0.00001:
break
print( 'new x:'+str(xn))
loop=loop+1
return xn
def f(x):
return x**2-4*math.sin(x)
def df(x):
return 2*x-4* math.cos(x)
def ddf(x):
return 2+4* math.sin(x)
x = newtons(df,ddf,3)
y = f(x)
print ('极值点为: '+str(x))
print('极小值为:'+str(y))
LM法
高斯牛顿法中采用的近似二阶泰勒展开只能展开点附近有较好的近似效果,所以我们可以将这个点扩充成一个范围,称为信赖区域,这种方法也称为信赖区域法。
三种算法的区别:
梯度下降法在寻找目标函数极小值时,是沿着反梯度方向进行寻找的。梯度的定义就是指向标量场增长最快的方向,在寻找极小值时,先随便定初始点(x0,y0)然后进行迭代不断寻找直到梯度的模达到预设的要求。但是梯度下降法的缺点之处在于:在远离极小值的地方下降很快,而在靠近极小值的地方下降很慢。
高斯牛顿法是一种非线性最小二乘最优化方法。其利用了目标函数的泰勒展开式把非线性函数的最小二乘化问题化为每次迭代的线性函数的最小二乘化问题。高斯牛顿法的缺点在于:若初始点距离极小值点过远,迭代步长过大会导致迭代下一代的函数值不一定小于上一代的函数值。
LM算法在高斯牛顿法中加入了因子μ,当μ大时相当于梯度下降法,μ小时相当于高斯牛顿法。(这儿我也不明白为什么,希望有大牛解答)。在使用Levenberg-Marquart时,先设置一个比较小的μ值,当发现目标函数反而增大时,将μ增大使用梯度下降法快速寻找,然后再将μ减小使用牛顿法进行寻找,代码的实现也可以用条件语句执行,当大于某个值,采用梯度下降算法,小于某个值,采用高斯牛顿法。
迭代公式: