机器学习中L1 L2正则化项(范式,惩罚项)
1. 什么是L1 L2?
正则化项,范式,惩罚项是不同学科范畴的学者的不同叫法,具体如下:
- 在机器学习称作正则化;
- 统计学领域称作惩罚项;
- 数学界会称作范数。
L1范数:L1范数就是曼哈顿距离,向量中每个元素绝对值的和 
L2范数:L2就是欧式距离,向量元素绝对值的平方和再开平方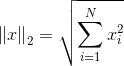
2. 在机器学习中L1 L2起到的作用是?
有如下比较普遍的解释:
- L1正则化:可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择;
- L2正则化:可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合。
从另一个角度理解:
- L1范数:在正则化的过程中会趋向于产生少量的特征,而其他的特征都是0(L1会使得参数矩阵变得稀疏)。因此L1不仅可以起到正则化的作用,还可以起到特征选择的作用。
- L2范数:L2范数是通过使权重衰减,进而使得特征对于总体的影响减小而起到防止过拟合的作用的。L2的优点在于求解稳定、快速。
备注:L2避免过拟合的原理是:让L2范数的规则项||W||2 尽可能小,可以使得W每个元素都很小,接近于零,但是与L1不同的是,不会等于0;这样得到的模型抗干扰能力强,参数很小时,即使样本数据x发生很大的变化,模型预测值y的变化也会很有限。
3. 正则化项(Regularization)为什么会起到上述作用?
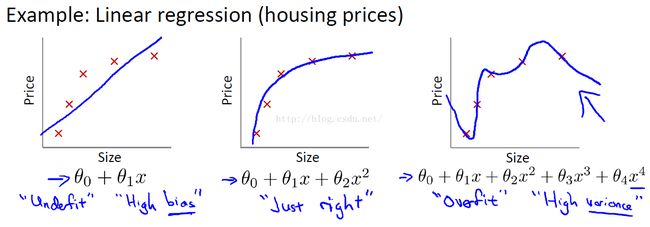
引入一个实际的房屋价钱预测案例作为理解正则化项的背景。
左图,欠拟合(underfitting),也称作High-bias,即对于当前数据集的拟合程度不够,欠拟合的特征是在训练集和测试集上的准确率都不好;
中图,拟合刚好的状态;
右边,过拟合(overfitting),也称作High variance,过拟合对于当前数据拟合得太好了,以至于模型只在当前的数据集上表现良好而在其他数据集上表现就不是那么好,所以过拟合的特征是在训练集上准确率很高而在训练集上表现一般。
解决过拟合主要有两种方法:
1.减少特征数量
2.正则化
因此,自然引入L1与L2范数正则化。
监督学习的过程可以概括为:最小化误差的同时规则化参数。最小化误差是为了让模型拟合训练数据,规则化参数是为了防止过拟合。参数过多会导致模型复杂度上升,产生过拟合,即训练误差很小,但测试误差很大,这和监督学习的目标是相违背的。所以需要采取措施,保证模型尽量简单的基础上,最小化训练误差,使模型具有更好的泛化能力(即测试误差也很小)。
3.1 L1正则化和特征选择
通常使参数稀疏都是用L1范数实现,L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。
L1范数为什么可以实现稀疏呢?
L1范数的表达式如下:
我们大概知道了L1可以实现稀疏,但为什么要稀疏?让我们的参数稀疏有什么好处呢?这引入两点:
1.特征选择(Feature Selection):
稀疏规则化能实现特征的自动选择。一般来说,![]() 的大部分元素(也就是特征)都是和最终的输出
的大部分元素(也就是特征)都是和最终的输出![]() 没有关系或者不提供任何信息的。在最小化目标函数的时候考虑
没有关系或者不提供任何信息的。在最小化目标函数的时候考虑![]() 这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确
这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确![]() 的预测。稀疏规则化算子的引入就是为了完成特征自动选择,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
的预测。稀疏规则化算子的引入就是为了完成特征自动选择,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
2.可解释性(Interpretability):
另一个青睐于稀疏的理由是,模型更容易解释。例如患某种病的概率是y,然后我们收集到的数据x是1000维的,也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型:y=w1x1+w2x2+…+w1000x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。通过学习,如果最后学习到的w就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。但如果1000个wi都非0,医生面对这1000种因素,累觉不爱。
加入L1正则化后,线性回归的代价函数为:
![]() 为原始的损失函数,加号后面的一项是L1正则化项,是正则化系数。
为原始的损失函数,加号后面的一项是L1正则化项,是正则化系数。
对它求w的偏导:
sgn(w)表示w的符号。对w进行更新:
可以看出,L1正则化是通过加上或减去一个常量![]() ,让w向0靠近;对比L2正则化,它使用了一个乘性因子
,让w向0靠近;对比L2正则化,它使用了一个乘性因子![]() 去调整权重,使权重不断衰减。
去调整权重,使权重不断衰减。
因此可以得出:当|w|很大时,L2对权重的衰减速度比L1大得多;当|w|很小时,L1对权重的缩小比L2快得多。
这也就解释了为什么L1正则能让模型变得稀疏。L1对于小权重减小地很快,对大权重减小较慢,因此最终模型的权重主要集中在那些高重要度的特征上,对于不重要的特征,权重会很快趋近于0。所以最终权重w会变得稀疏。
3.2 L2正则化和过拟合
L2范数也被称为权重衰减(weight decay),线性回归中应用L2范数也被称为岭回归Ridge Regression,在其他文献中也有将L2范数称为Tikhonov正则。首先我们通过线性回归来看一下L2范数。
线性回归的代价函数为:
加入L2正则化后,代价函数变为:
如何理解上式?
把上式分为两部分,左边部分即为原始的代价函数,右边部分为L2正则化项(注意:正则化项中不包含w0)。lambda为超参数,通常会取一个较大的数。
为了最小化整个代价函数,当lambda是固定的,那么就要减小![]() 到
到![]() 的值。对于上图中的那种过拟合状态,加入正则项后,
的值。对于上图中的那种过拟合状态,加入正则项后,![]() 至
至![]() 均会减小,也就是使得权重衰减,这样就会降低高阶项对于整个函数的影响,使得估计函数变得比较平滑。
均会减小,也就是使得权重衰减,这样就会降低高阶项对于整个函数的影响,使得估计函数变得比较平滑。
可以想象一种极端的情况,如果lambda为无穷大,那么![]() 至
至![]() 趋近于0,那么整个式子就只剩一个
趋近于0,那么整个式子就只剩一个![]() ,为一条和y轴垂直的直线,这种状态为严重的欠拟合状态。可以看到,当lambda为0时,即为原来的状态,此时过拟合,而当lambda过大时又会导致欠拟合,所以会有一个恰当的lambda使得模型处于既不过拟合又不欠拟合的状态。
,为一条和y轴垂直的直线,这种状态为严重的欠拟合状态。可以看到,当lambda为0时,即为原来的状态,此时过拟合,而当lambda过大时又会导致欠拟合,所以会有一个恰当的lambda使得模型处于既不过拟合又不欠拟合的状态。
加入正则项后,求偏导,梯度下降算法更新每个![]() ,重复这个过程:
,重复这个过程:
repeat{
}
可以看到,由于学习速率![]() >0,
>0, ![]() >0(而且这两个值一般都是很小的正数),所以1-a <1,即每次
>0(而且这两个值一般都是很小的正数),所以1-a <1,即每次![]() 在更新的时候都会缩小一下。
在更新的时候都会缩小一下。
上面我们对线性回归应用的正则化就是L2正则化,通常被称为权重衰减(weight decay)的L2参数范数惩罚。在其他文献或论文中,L2有时也被称为岭回归ridge regression和Tikhonov正则。
正如在线性回归中的应用,L2参数正则化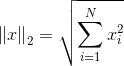 就是在损失函数中加入一个L2范数和一个超参数lambda。L2范数对于向量w中的各个数先求平方再加和,而超参数lambda则用于控制参数惩罚的程度。
就是在损失函数中加入一个L2范数和一个超参数lambda。L2范数对于向量w中的各个数先求平方再加和,而超参数lambda则用于控制参数惩罚的程度。
4. L1和L2正则化的直观理解?
4.1模型空间的限制:
实际上,对于L1和L2规则化的代价函数来说,我们可以写成以下形式:
也就是说,我们将模型空间限制在w的一个L1-ball 中。为了便于可视化,我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解:
如上图所示,假设w是一个二维的向量,则目标函数可以用一圈圈等值线表示,约束条件用图中黑线表示,而我们要找的最优解,就在等值线和约束线第一次相交的地方。
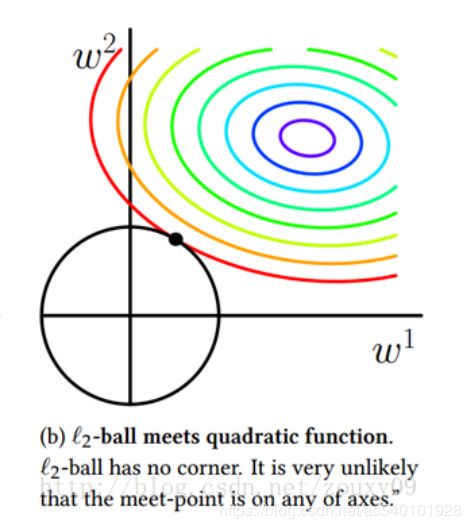
可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,而目标函数的测地线除非位置摆得非常好,大部分时候都会在角的地方相交。
左图中黑线是L1正则化,在特征为二维时,约束线是一个菱形,等值线极有可能最先与顶点相交,在这种情况下有一个维度的特征就会为0,这就带来了稀疏。当特征的维度变高,坐标轴上角与边都会变多,这更会加大等值线与他们先相交的概率,从而导致了稀疏性。注意到在角的位置就会产生稀疏性,例如图中的相交点就有w1=0。
相比之下,L2-ball 就没有这样的性质,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性,而L2-regularization 不行的原因了。
右图中黑线是L2正则化,在特征为二维时,它的约束线是一个圆形,等值线可能与它任意一个位置的点首先相切,这个切点在坐标轴上的概率大大 减小,从而不太容易导致稀疏。
因此,一句话总结就是:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。
4.2.下降速度。
L1和L2都是规则化的方式,我们将权值参数以L1或者L2的方式放到代价函数里面去。然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程,L1和L2的差别就在于这个“坡”不同,如下图:L1就是按绝对值函数的“坡”下降的,而L2是按二次函数的“坡”下降。所以实际上在0附近,L1的下降速度比L2的下降速度要快。所以会非常快得降到0。
5.正则化参数的选择
通常越大的![]() 可以让代价函数在参数为0时取到最小值。下面是一个简单的例子,这个例子来自Quora上的问答。为了方便叙述,一些符号跟这篇帖子的符号保持一致。
可以让代价函数在参数为0时取到最小值。下面是一个简单的例子,这个例子来自Quora上的问答。为了方便叙述,一些符号跟这篇帖子的符号保持一致。
假设有如下带L1正则化项的代价函数:
![]()
其中x是要估计的参数,相当于上文中提到的w。注意到L1正则化在某些位置是不可导的,当λ足够大时可以使得F(x)在x=0时取到最小值。如下图:
分别取λ=0.5 和λ=2,可以看到越大的λ越容易使F(x)在x=0时取到最小值。
·感谢一些作者的分享:
参考阅读了一些网络的blog,将URL附在下列:
https://www.cnblogs.com/crawer-1/p/8550302.html
https://blog.csdn.net/weiyongle1996/article/details/78161512
https://www.jianshu.com/p/4bad38fe07e6
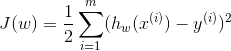
![J(w)=\frac{1}{2}\sum_{i=1}^{m} \left [ (h_{w}(x^{(i)})-y^{(i)})^{2}+\lambda \sum_{i=1}^{n}w _{j}^{2}\right ]](http://img.e-com-net.com/image/info8/b35a2bae6d964784abb30b29d44e400c.gif)
![w_{0}:=w_{0}-\alpha \left [ \sum_{i=1}^{m}[(h_{w}(x^{(i)})-y^{(i)})x_{0}^{(i)} \right ]](http://img.e-com-net.com/image/info8/11921478b928402c98d2de46c3b180e1.gif)
![w_{j}:=w_{j}-\alpha \left [ \sum_{i=1}^{m}[(h_{w}(x^{(i)})-y^{(i)})x_{0}^{(i)}-\lambda w _{j} \right ]](http://img.e-com-net.com/image/info8/bf976615a9b542249e57d92032b313f1.gif)