无意间看到了介绍运动曲线的一个很有趣的网站cubic-bezier,在cubic-bezier.com网站中简单绘制需要形状的曲线,然后选择线性曲线作为参考,就可以查看方块的运动变化情况。借着这个机会,我们就来聊一聊一些动画中的运动曲线吧!
运动图例
我们都知道时间是一秒一秒过去的,也就是线性的,匀速前进的。如果属性值从起始值到结束值是匀速变化的话,那么整个动画看起来就是慢慢地均匀地变化着。但是,如果我们想让动画变得很快或者变得很慢怎么办?答案是我们可以通过“篡改时间”来完成这个任务!实际上就是一条函数曲线。
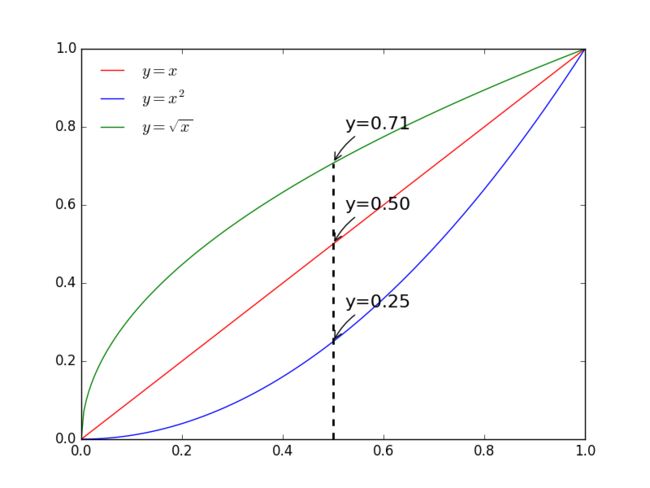
如下图所示,x轴表示时间的比率,y轴表示属性值。假设属性值是从0变化到1,默认情况下线性插值器就和曲线y=x一样,在时间t的位置上的值为f(t)=t。但是,当我们设置函数y=x2或者y=x(0.5)时,动画的效果就截然不同啦。在t=0.5的时刻,y=x^2=0.25 < 0.5,表示它将时间推迟了;而y=x^(0.5)=0.71 > 0.5,表示它将时间提前了。
此外,仔细观察曲线的斜率不难发现,曲线y=x2的斜率在不断增加,说明变化越来越快,作用在View组件上就是刚开始挺慢的,然后不断加速的效果;而曲线y=x(0.5)的斜率在不断减小,说明变化越来越慢,作用在View组件上就是刚开始挺快的,然后不断减速的效果。
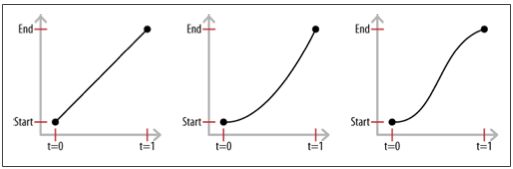
linear,ease in以及ease in out
注:t为时间,start为起点,end为结束点
linear是线性运动,ease 规定慢速开始,然后变快,然后慢速结束的过渡效果(cubic-bezier(0.25,0.1,0.25,1)); ease-in 规定以慢速开始的过渡效果; ease-out 规定以慢速结束的过渡效果(等于 cubic-bezier(0.42,0,1,1)); ease-in-out 规定以慢速开始和结束的过渡效果(等于 cubic-bezier(0.42,0,0.58,1))。
一个标准的3次贝塞尔曲线需要4个点:起始点、终止点(也称锚点)以及两个相互分离的中间点。
三次贝塞尔曲线指令:C x1 y1, x2 y2, x y,两个控制点(x1,y1)和(x2,y2),(x,y)代表曲线的终点。字母C表示特定动作与行为,这里需要大写,表示标准三次方贝塞尔曲线。cubic-bezier, 直译为“立方-贝塞尔”,实际上就是指的标准三次方贝塞尔曲线。
cubic-bezier(.25,.1,.25,1)
.25,.1这个坐标对于起点连接的那个锚点;.25,1这个坐标对于终点头上那根天线顶端那个点。有人会疑问,动画那个cubic-bezier值好像只有两个点诶~~那是因为动画贝塞尔曲线的起点和终点已经固定了,分别是(0,0)和(1,1)。
cubic-bezier 公式不是简单的 y= x 公式,而是引入了第三个变量 t,由于动画中关键在于计算比例,即在总时间的某个时间点百分比得到相应的值相对于最终值的比例,那么只需要得到 0,1 区间的曲线即可。 而 [x,y] -> [0,1] 内的曲线则是通过 t 在 0,1 内连续变化而得到:
其中 P0, P1 ,P2, P3 都为两维 xy 向量。
cubic_bezier 曲线限制了首尾两控制点的位置,通过调整中间两控制点的位置可以灵活得到常用的动画效果。动画所做的事情就是把 x 轴当做时间比例,根据曲线得到 y 轴对应的值,并更新到动画对象中去。
那么,我们用代码实现就是这样:
linear:
float LinearTween(float t, float start, float end)
{
return t * start + (1 - t) * end;
}
ease in:
float QuadraticEaseIn(float t, float start, float end)
{
return LinearTween(t * t, start, end);
}
ease in out:
float QuadraticEaseInOut(float t, float start, float end)
{
float middle = (start + end) / 2;
t = 2 * t;
if (t <= 1) return LinearTween(t * t, start, middle);
t -= 1;
return LinearTween(t * t, middle, end);
}