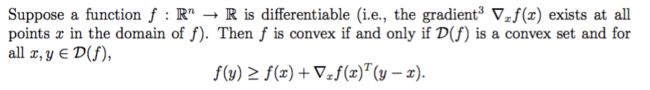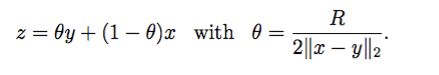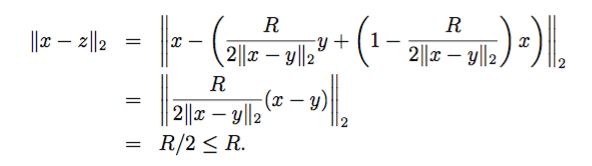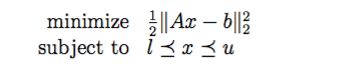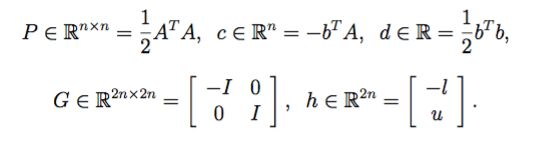关于凸优化

本文结构：

• 凸优化有什么用？
• 什么是凸优化？

---

凸优化有什么用？

鉴于本文中公式比较多，先把凸优化的意义写出来吧，就会对它更有兴趣。

我们知道在机器学习中，要做的核心工作之一就是根据实际问题定义一个目标函数，然后找到它的最优解。

不过求解这种优化的问题其实是很难的，但是有一类问题叫做凸优化问题，我们就可以比较有效的找到全局最优解。

例如，SVM 本身就是把一个分类问题抽象为凸优化问题，利用凸优化的各种工具（如Lagrange对偶）进行求解和解释。深度学习中关键的算法反向传播（Back Propagation），本质也是凸优化算法中的梯度下降算法。

凸优化的价值也在于思维转变，当我们在现实生活中遇到计算量接近无穷大的问题时，我们要想办法将模型转换成“凸优化问题”，因为凸优化已经相对嚼得比较烂，所以只要问题转化成凸优化，我们就可以分布迭代去运算。

当然现实中绝大部分优化问题并不是凸优化问题，但是凸优化非常重要, 因为：

• 还是有相当一部分问题是或等价于凸优化问题，例如下面会举例说明 SVM，最小二乘等。
• 大部分凸优化问题解起来比较快。
• 很多非凸优化或NP-Hard的问题可以转化（并非是等价的）为P的凸优化问题。并给出问题的界或近似。例如用对偶（Duality），松弛（Relaxation）等方法将一个优化问题转化为凸优化。

---

什么是凸优化？

关于凸优化，有几个基础概念：凸集，凸函数，凸优化问题，局部最优和全局最优。以及一个很重要的性质，就是所有局部最优点都是全局最优的

1. 凸集

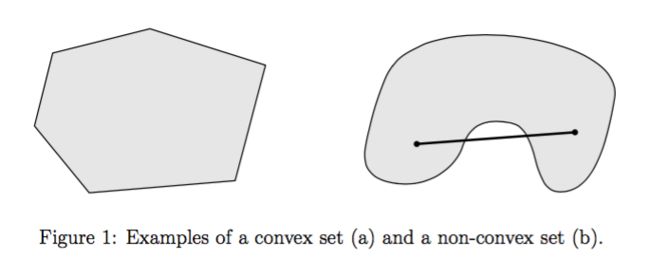
意思是对这个集合的任何两个元素，我们如果画一条线，那么这线上的所有元素仍然属于这个集合：

下面这几个例子都是凸集：

Rn，因为对任意 x, y ∈ Rn, θx + (1 − θ)y ∈ Rn

Rn+ = {x : xi ≥ 0 ∀i = 1,…,n}，因为 (θx+(1−θ)y)i =θxi +(1−θ)yi ≥0 ∀i。

范数球，∥ · ∥ 例如 {x: ∥x∥ ≤ 1}

映射子空间 Affine subspaces： {x ∈ Rn : Ax = b}

多面体 polyhedra： {x ∈ Rn : Ax ≼ b}，即 Ax 的每个元素小于或等于 b 的对应元素

凸集的交集

半正定矩阵 Positive semidefinite matrices：A = AT 且 for all x ∈ Rn, xT Ax ≥ 0.

在文献中有详细的证明：
http://cs229.stanford.edu/section/cs229-cvxopt.pdf

只需要按照凸集的定义，任取这个集合的两个元素，以及 0 ≤ θ ≤ 1，如果可以证明 θx+(1−θ)y 仍然属于这个集合，那么它就是凸集

---

2. 凸函数：

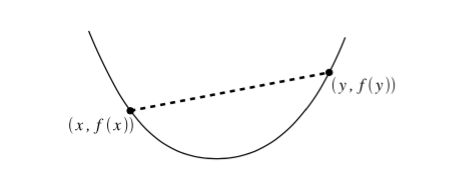
它的含义就是在这个函数上任意取两个点，在它们之间画一条线，那么这两点之间的函数上的值需要在这条线以下。：

如何验证某个函数是否为凸函数呢？

最基本的，我们可以用凸度的一阶二阶条件：

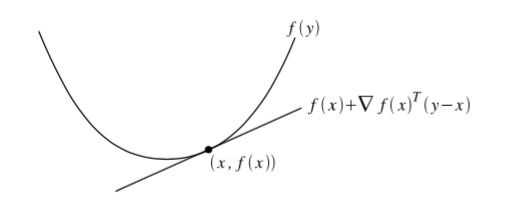
一阶条件的含义就是，如果我们在这个函数上的任意一点画出它的切线，那么这条切线上的所有点都将在函数的下面。：

二阶条件中如果是一维的话，就相当于函数的二阶导数总是非负的。：

≽ 此处意思为半正定。

下面这几个例子都是凸函数
可以根据二阶条件，即证明它们的二阶导数非负来判断：

Exponential. Letf :R→R,f(x)=e^ax for any a ∈ R.

Negative logarithm. Let f : R → R, f(x) = −logx {x : x > 0}，

Affinefunctions. Letf:Rn →R,f(x)=bT x + c for some b ∈ Rn,c ∈ R

当然还有下面两个可以直接通过凸函数的定义和不等式来证明：

Norms. Let f : Rn → R be some norm on Rn

Nonnegative weighted sums of convex functions

---

3. 凸优化问题：

就是我们想要找到凸集 C 中的某个 x 来使 f 达到极小：

minimize f (x)
subject to x ∈ C

其中 f 为凸函数，C 为凸集，

4. 局部最优和全局最优

局部最优的意思是如果 x 这个点是函数的局部极小值点，那么我们可以找到一个半径 R，在以 x 为中心以 R 为半径的球内的任何一个点，它的函数值都会大于这个极小值。

全局最优就是 x 这点的函数值就是在定义域中函数达到的最小值。

5. 性质

对于凸优化问题，有一个很重要的性质，就是所有局部最优点都是全局最优的。

为什么呢，证明如下：

设 x 为一个局部极小值点，那么我们可以找到另外的一个点 y，使得 f(x) > f(y)

这样的话，我们找到一个 z 为：

那么 z 就在 x 的这个半径 R 内：

但是由凸函数定义可得：

即我们在半径 R 内，找到了一个 z ，它的函数值要比 x 的还要小，这与 x 是局部极小值矛盾，所以 x 不可能是局部极小值，只可以是全局的。

下面这几个例子都是凸优化问题：

Linear Programming

Quadratic Programming

Quadratically Constrained Quadratic Programming

Semidefinite Programming

---

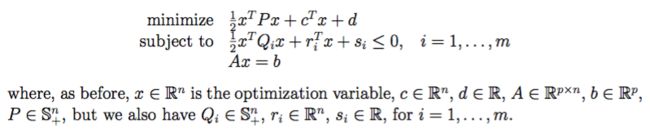
那么这些有什么用呢？

让我们用常见的算法举例，

1. SVM 的优化目标如下：

如果我们根据下面的形式，定义了 x，P，c，G，h，X，y，

那么 SVM 的优化目标就可以写成 Quadratic Programming 的形式：

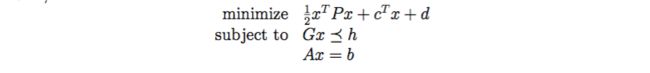
所以这是个凸优化问题，
当然了我们可以简单地根据 SVM 具有二次的优化目标，以及线性的限制条件来判断，而无需转化成标准形式。

2. 最小二乘的优化目标：

如果我们做如下定义，可以看出它也是个 Quadratic Programming：

---

当我们拿到了一个凸的优化函数时，那么就有一大套公式定理可以帮我们解决问题了。
因为对凸优化的问题，在基础数学上面已经有了很多解决方法，例如可以将凸优化问题Lagerange做对偶化，然后用Newton、梯度下降算法求解等等。

推荐凸优化入门资源：

• book Convex Optimization by Stephen Boyd and Lieven Vandenberghe (available for free online),
• EE364，a class taught here at Stanford by Stephen Boyd

参考：
http://cs229.stanford.edu/section/cs229-cvxopt.pdf
https://www.zhihu.com/question/24641575

---

推荐阅读
历史技术博文链接汇总
也许可以找到你想要的