从零开始带你了解商业数据分析模型——线性回归模型

本文主要分为线性回归模型理论介绍和实战演练，将分两篇文章发，感兴趣的小伙伴可以关注我们呀~

1. 摘要

随着数据导向型决策、数据科学、大数据分析等话题日益火热，各行各业都开始关注数据分析这个课题。数字化转型成了很多企业在未来十年的重大举措。企业如何利用现有庞大的数据辅助决策，以及通过数据分析帮助企业盈利或削减开支成了越来越多部门关注的难题。

除了上述提到的行业内部的业务理解，从业人士对数据科学技术细节的理解，对数据建模的落地实施也成了当下的难点。

我打算写一个系列文章，旨在帮助非科班从业人士了解常见的商业数据分析模型。内容涵盖模型的基本介绍、优劣势分析、常见使用案例，以及如何在具体平台中实施相应的模型。

此文为系列文章的第一篇，从大家最耳熟能详的线性回归模型开始说起，并以Altair Knowledge Studio为平台，介绍线性回归在实际中如何应用，给大家在实战中贡献一点参考。

2. 线性回归模型

2.1. 什么是回归

在讨论线性回归之前，我希望用一些篇幅来讨论什么是回归模型。作为最基础的机器学习算法，回归模型最早发表于1805年，用以研究行星轨道距离太阳的距离。随着后续两百多年的发展，回归模型的族群逐渐壮大。现在常见的族员有线性回归，逻辑回归，多项式回归，岭回归，套索回归等等。

简而言之，当想要研究自变量与因变量之间的关系时，回归模型往往是我们的首选。那么，什么又叫做自变量，什么又是因变量呢？

2.2. 自变量与因变量

通常来说，自变量是指可以通过研究者主动操作而改变的因素或者条件，它可以视为使得因变量变化的原因。因变量是指会随着自变量变化，而变化的因素。而模型则是通过自变量和因变量的历史数据，运用适当的统计算法所寻求出来的一套规律。通常在回归模型中，我们可以拥有多个自变量，但是因变量只能有一个。

这样的描述可能也不是特别清晰。不过没关系，我们可以通过下面的一个简单例子来辅助理解。

比如我们现在想要研究子女的身高和父母的身高是否存在一定的关系。我们想要寻找的关系，就是模型。父母的身高就是自变量。而子女的身高就是因变量。

2.3. 一元线性回归

有了上述的基本介绍，我们接下来看看最简单的一种线性回归模型
– 一元线性回归模型。这里的一元指的是模型中只含有一个自变量。它的表达式可以写作

为方便理解，大家可以将 y 视为子女的身高（单位是cm），x视为父亲的身高（单位是cm）。其中的 w0 与w1 叫做模型的参数，也是我们需要通过统计算法寻找的值。大家可以将参数理解为权重。比如当w1 = 0.05时，我们可以认为，如果父亲的身高每增加一厘米，子女的身高就可能增加0. 05厘米。相应的，w0 则类似于子女的保底身高。因为孩子的身高还会取决于现今的生活环境和营养水平等因素，该参数则涵盖了非遗传角度考量的绝大多数因素。最后的随机误差项则是代表了统计学中的不确定性。它代表的含义是：即便拥有同样遗传因素，在相同条件下生长的两个孩子的身高大概率也会是不同的。

接下来我们借助一个简单的案例来了解这个过程。假如我们已知了6对父亲与子女身高的数据如下（父亲的身高, 子女的身高）。

（160,162），（165,167），（170,168.5），（175,179），（180,182），（185,184）.

将其画作散点图，并对其进行任意拟合。我们可以发现这些点可以拟合出无数条可能的模型结果，分别由每条线所对应的不同的w0 与w1和组成。 不同的线所对应的斜率和截距也各有不同。如何从这些拟合结果中选出最优的那个结果，成了我们接下来的讨论话题。

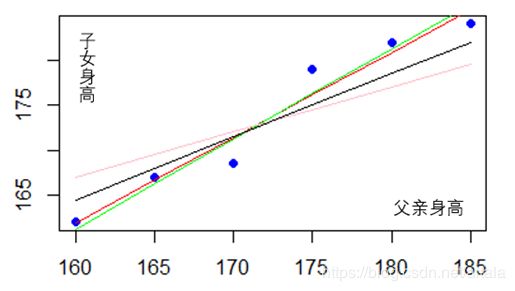
要知道哪一条结果模型拟合的最好，其中一个方法就是最小化预测出来的身高值和真实的身高值之差的平方和，数学表达式为

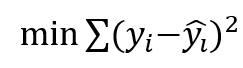
比如说，我们得出了其中一条拟合模型为：y = 10.6 + 0.95 * x。我们用（160，162）这组数据举例。其中的真实值yi 就是162，我们的预测值则是 10.6 + 0.95*160 = 162.6。 这组数据的差值平方就是0.36。
全部的六组数据计算完成后，我们就可以得出这个拟合模型的差值平方和为23.75。

类似的，我们可以计算出别的拟合模型的差值平方和。最后该数值最小的拟合模型既是我们所寻找的最佳方案。

2.4. 多元线性回归

我们上面所展示的案例，在实际生活之中基本不可能出现。因为它过于简单也过于理想化。不过它足够帮助大家了解清楚线性回归的基本概念了。

多元线性回归可以视为简单的一元线性回归的补充。同样拿上述的例子说明，子女的身高很可能也取决于母亲的身高，当地的平均身高，子女青春期的锻炼程度等因素。如果数据允许的话，我们可以用一个多元线性回归表达式来概述这个模型。
多元线性回归表达式的意义和寻找最佳拟合的方法和一元线性回归类似，我在此也就不过多赘述了。

2.5. 线性回归的优劣分析和模型假设

虽然线性回归是最常见的一种回归模型，也是绝大多数科班生接触到的第一个统计模型，但是这并不代表了所有问题都适合用线性回归来解决，也不代表了任何数据都可以直接输入到线性回归之中。

线性回归的优点特别直接：

i. 模型建立速度快。因为它并不包含复杂的算法过程，所以就算我们有庞大的数据量，线性回归也能够很快的拟合出最佳参数；

ii. 可解释性高。我们可以明确的指出线性回归里面包含的自变量，以及通过参数的大小解释不同自变量和因变量之间的线性关系。这是很多复杂模型所无法做到的。

然而线性回归的缺点更加直接：它只适用于分析自变量和因变量之间的线性关系。所以它不是适用于非线性关系之间的解析。且它仅适合处理因变量是连续型/数值型变量的数据。

与此同时，为了运用线性回归模型，我们还应确保我们的历史数据符合以下的假设条件：

i. 随机扰动项与自变量之间不相关.
ii. 随机扰动项服从平均值为0的正态分布且互不相关

iii. 自变量之间不存在完全共线性，也就是说没有精确的线性关系。

2.6. 线性回归的商业实用案例

作为最常见的模型之一，各行各业之中都可以找到线性回归的身影。

比如在快消行业，我们想要去研究特定的市场活动，价格变化，促销活动，季节气候等因素对某一商品的销量影响；

比如在体育竞技行业，我们想去研究球队，地区，身体因素，教练因素，赞助商状况对一位运动员比赛得分的影响；

再比如在银行信用卡行业，我们想去研究学历，收入情况，家庭情况，年龄等因素对信用卡持有人是否能够准时还款的影响。

随着算法模型的发展，线性回归在日常商业中的应用案例逐渐减少，取而代之的是逻辑回归，支持向量机，深度学习，决策树，随机森林等模型。我们也会在后续的文章中对这些模型进行一一讲解。

希望大家能够借住线性回归模型打开对数据分析建模的兴趣。随着讲解的深入，最好还能够帮助大家在自己的行业里面解决现有的问题，完成数字化转型的重要一步。

接下来一篇将介绍如何用Altair KnowledgeStudio平台进行线性回归。