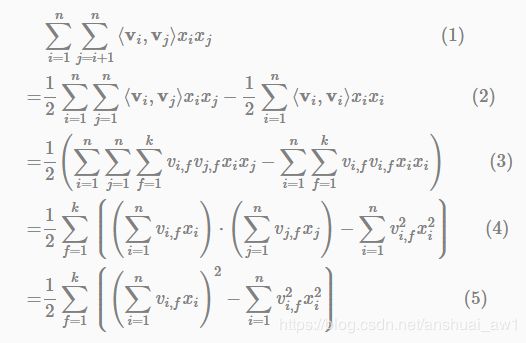（一）因式分解机（Factorization Machine，FM）原理及实践

因子分解机（Factorization Machine），是由Konstanz大学（德国康斯坦茨大学）Steffen Rendle（现任职于Google）于2010年最早提出的，旨在解决大规模稀疏数据下的特征组合问题。原论文见此。

不久后，FM的升级版模型场感知分解机（Field-aware Factorization Machine，简称FFM）由来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员提出。通过引入field的概念，FFM把相同性质的特征归于同一个field。

本次系列博客主要深入讲解了FM和FFM的原理，并给出实践。

本篇的主要内容是FM。FFM的内容稍后整理。

一、前言

FM旨在解决大规模稀疏数据下的特征组合问题，那么大规模稀疏数据是怎么来的呢？在现实生活中，以用户访问某网站的日志为例，我们可以发现许多特征是类别特征，如用户访问的是频道（channel）信息，如”news”, “auto”, “finance”等。

假设channel特征有10个取值，分别为{“auto”,“finance”,“ent”,“news”,“sports”,“mil”,“weather”,“house”,“edu”,“games”}。部分训练数据如下：

特征ETL过程中，需要对categorical型特征进行one-hot编码（独热编码），即将categorical型特征转化为数值型特征。channel特征转化后的结果如下：

可以发现，由one-hot编码带来的数据稀疏性会导致特征空间变大。上面的例子中，一维categorical特征在经过one-hot编码后变成了10维数值型特征。真实应用场景中，未编码前特征总维度可能仅有数十维或者到数百维的categorical型特征，经过one-hot编码后，达到数千万、数亿甚至更高维度的数值特征在业内都是常有的。

此外也能发现，特征空间增长的维度取决于categorical型特征的取值个数。在数据稀疏性的现实情况下，我们如何去利用这些特征来提升learning performance？

或许在学习过程中考虑特征之间的关联信息。针对特征关联，我们需要讨论两个问题：1. 为什么要考虑特征之间的关联信息？2. 如何表达特征之间的关联？

1. 为什么要考虑特征之间的关联信息？

   大量的研究和实际数据分析结果表明：某些特征之间的关联信息（相关度）对事件结果的的发生会产生很大的影响。从实际业务线的广告点击数据分析来看，也证实了这样的结论。

2. 如何表达特征之间的关联？

   表示特征之间的关联，最直接的方法的是构造组合特征。样本中特征之间的关联信息在one-hot编码和浅层学习模型（如LR、SVM）是做不到的。目前工业界主要有两种手段得到组合特征：
   ①、人工特征工程（数据分析＋人工构造）；
   ②、通过模型做组合特征的学习（深度学习方法、FM/FFM方法）

FM就可以学习特征之间的关联。$x_i{x}_j$ 表示特征$x_i$和$x_j$的组合，当$x_i$和$x_j$都非零时，组合特征$x_i{x}_j$才有意义。

接下来，我们以二阶多项式模型（degree=2时）为例，来分析和探讨FM原理和参数学习过程。

二、FM模型表达

为了更好的介绍FM模型，我们先从多项式回归、交叉组合特征说起，然后自然地过度到FM模型。

2.1 二阶多项式回归模型

我们先看二阶多项式模型的表达式：
$$\hat{y}(x):=\underset{\text{线性回归}}{w_0+\sum _{i=1}^n{w}_i{x}_i}+\underset{\text{交叉项（组合特征）}}{\sum _{i=1}^n\sum _{j=i+1}^n{w}_{ij}{x}_i{x}_j}\text{(1)}$$

其中，$n$表示特征维度，截距$w_0\in R,w＝\{w_1,w_2,\cdots ,w_n\}\in R^n,w_{ij}\in R^{n\times n}$为模型参数。

从公式(1)可知，交叉项中的组合特征参数总共有$\frac{n(n-1)}{2}$个。在这里，任意两个交叉项参数$w_{ij}$都是独立的。然而，在数据非常稀疏的实际应用场景中，交叉项参数的学习是很困难的。why？

因为我们知道，回归模型的参数$w$的学习结果就是从训练样本中计算充分统计量（凡是符合指数族分布的模型都具有此性质），而在这里交叉项的每一个参数$w_{ij}$的学习过程需要大量的$x_i$、$x_j$同时非零的训练样本数据。由于样本数据本来就很稀疏，能够满足“$x_i$和$x_j$都非零”的样本数就会更少。训练样本不充分，学到的参数$w_{ij}$就不是充分统计量结果，导致参数$w_{ij}$不准确，而这会严重影响模型预测的效果（performance）和稳定性。How to do it ?

那么，如何在降低数据稀疏问题给模型性能带来的重大影响的同时，有效地解决二阶交叉项参数的学习问题呢？矩阵分解方法已经给出了解决思路。

根据矩阵分解的启发，如果把多项式模型中二阶交叉项参数$w_{ij}$组成一个对称矩阵$W$（对角元素设为正实数），那么这个矩阵就可以分解为$W=V{V}^T$，$V\in R^{n\times k}$称为系数矩阵，其中第$i$行对应着第$i$维特征的隐向量 。即，每一个特征都有一个长度为$k$的隐变量替代。

将每个交叉项参数$w_{ij}$用隐向量的内积$⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩$表示，是FM模型的核心思想。下面对FM模型表达式和参数求解过程，给出详细解读。

2.2 FM模型表达

这里我们只讨论二阶FM模型（degree＝2），其表达式为：
$$\hat{y}(\mathbf{x}):=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j\text{(1)}$$

其中，$v_i$表示第$i$特征的隐向量，$⟨\cdot ,\cdot ⟩$表示两个长度为$k$的向量的内积，计算公式为：
$$⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩:=\sum _{f=1}^k{v}_{i,f}\cdot v_{j,f}\text{(2)}$$

公式解读：

• 线性模型＋交叉项

  直观地看FM模型表达式，前两项是线性回归模型的表达式，最后一项是二阶特征交叉项（又称组合特征项），表示模型将两个互异的特征分量之间的关联信息考虑进来。用交叉项表示组合特征，从而建立特征与结果之间的非线性关系。

• 交叉项系数 → 隐向量内积

  由于FM模型是在线性回归基础上加入了特征交叉项，模型求解时不直接求特征交叉项的系数$w_{ij}$（因为对应的组合特征数据稀疏，参数学习不充分），故而采用隐向量的内积$⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩$表示$w_{ij}$。

  具体地，FM求解过程中的做法是：对每一个特征分量$x_i$引入隐向量${\mathbf{v}}_i＝(v_{i,1},v_{i,2},\cdots ,v_{i,k})$，利用$v_i{v}_j^T$内积结果对交叉项的系数$w_{ij}$进行估计，公式表示：${\hat{w}}_{ij}:=v_i{v}_j^T$。

隐向量的长度$k$称为超参数$(k\in N^{+},k\ll n)$的含义是用$k$个描述特征的因子来表示第$i$维特征。根据公式(1)，二阶交叉项的参数由$n\cdot n$个减少到$n\cdot k$个，远少于二阶多项式模型中的参数数量。即原来的系数$w_{ij}$为$n\cdot n$个，而现在每一个$x_i$均由隐向量表示，故参数个数就是$V\in R^{n\times k}$，$n\cdot k$个。

此外，参数因子化表示后，使得$x_h{x}_i$的参数与$x_i{x}_j$的参数不再相互独立。这样我们就可以在样本稀疏情况下相对合理的估计FM模型交叉项的参数。这是因为：

$x_h{x}_i$与$x_i{x}_j$的系数分别为$⟨{\mathbf{v}}_h,{\mathbf{v}}_i⟩$和$⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩$，他们之间有共同项$v_i$。也就是说，所有包含$x_i$的非零组合特征（存在某个$j\ne i$，使得$x_i{x}_j\ne 0$）的样本都可以用来学习隐向量$v_i$，这在很大程度上避免了数据稀疏行造成参数估计不准确的影响。即只要某个样本的某2个特征不同时为0，这时这个样本就可以用来学习这某2个特征。

原论文中还提到FM模型的应用场景，并且说公式(1)作为一个通用的拟合模型（Generic Model），可以采用不同的损失函数来解决具体问题。比如：

三、FM参数学习

公式(1)中直观地看，FM模型的复杂度为$O(k{n}^2)$，但是通过下面的等价转换，可以将FM的二次项化简，其复杂度可优化到$O(kn)$。即：
$$\sum _{i=1}^n\sum _{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j=\frac{1}{2}\sum _{f=1}^k⟮{\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2⟯(3)$$

下面给出详细推导：

解读第（1）步到第（2）步，这里用$A$表示矩阵${\sum }_{i=1}^n{\sum }_{j=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j$的上三角元素，$B$表示对角线上的交叉项系数。由于矩阵${\sum }_{i=1}^n{\sum }_{j=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j$是一个对称阵，所以下三角与上三角相等，有下式成立：

$A=\frac{1}{2}(2A+B)-\frac{1}{2}B.\underline{A={\sum }_{i=1}^n{\sum }_{j=i+1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j};\underline{B=\frac{1}{2}{\sum }_{i=1}^n⟨{\mathbf{v}}_i,{\mathbf{v}}_i⟩x_i{x}_i}(4)$

接着，我们把公式（3）替换公式（1）中的交叉特征项，有：

$$\hat{y}(\mathbf{x}):=w_0+\sum _{i=1}^n{w}_i{x}_i+\frac{1}{2}\sum _{f=1}^k⟮{\left(\sum _{i=1}^n{v}_{i,f}{x}_i\right)}^2-\sum _{i=1}^n{v}_{i,f}^2{x}_i^2⟯\text{(5)}$$

如果用随机梯度下降（Stochastic Gradient Descent）法学习模型参数。那么，模型各个参数的梯度如下：
$$\frac{\partial }{\partial \theta }y(\mathbf{x})=\{\begin{array}{ll}1,& \text{if}\theta \text{is}{w}_0\text{(常数项)}\\ x_i& \text{if}\theta \text{is}{w}_i\text{(线性项)}\\ x_i{\sum }_{j=1}^n{v}_{j,f}{x}_j-v_{i,f}{x}_i^2,& \text{if}\theta \text{is}{v}_{i,f}\text{(交叉项)}\end{array}(6)$$

其中， $v_{j,f}$是隐向量$v_j$的第$f$个元素。

由于${\sum }_{j=1}^n{v}_{j,f}{x}_j$只与$f$有关，在参数迭代过程中，只需要计算第一次所有$f$的${\sum }_{j=1}^n{v}_{j,f}{x}_j$，就能够方便地得到所有$v_{i,f}$的梯度。显然，计算所有$f$的${\sum }_{j=1}^n{v}_{j,f}{x}_j$的复杂度是$O(kn)$；已知${\sum }_{j=1}^n{v}_{j,f}{x}_j$时，计算每个参数梯度的复杂度是$O(n)$；得到梯度后，更新每个参数的复杂度是 $O(1)$；模型参数一共有$nk+n+1$个。因此，FM参数训练的时间复杂度为$O(kn)$。

四、FM总结

上面我们主要是从FM模型引入（多项式开始）、模型表达和参数学习的角度介绍的FM模型。我们总结FM模型的核心作用，可以概括为以下3个：

1、FM降低了交叉项参数学习不充分的影响

one-hot编码后的样本数据非常稀疏，组合特征更是如此。为了解决交叉项参数学习不充分、导致模型有偏或不稳定的问题。作者借鉴矩阵分解的思路：每一维特征用$k$维的隐向量表示，交叉项的参数$w_{ij}$用对应特征隐向量的内积表示，即$⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩$（也可以理解为平滑技术）。这样参数学习由之前学习交叉项参数$w_{ij}$的过程，转变为学习$n$个单特征对应$k$维隐向量的过程。

很明显，单特征参数（$k$维隐向量$v_i$）的学习要比交叉项参数$w_{ij}$学习得更充分。示例说明：

<女性，汽车>的含义是女性看汽车广告。可以看到，单特征对应的样本数远大于组合特征对应的样本数。训练时，单特征参数相比交叉项特征参数会学习地更充分。也就是说，如果我们还是用$w_{ij}$的方式去学习<女性，汽车>，那么只有500个样本，而用单特征参数（$k$维隐向量$v_i$）的方式去学习就会有大于30000个样本。

因此，可以说FM降低了因数据稀疏，导致交叉项参数学习不充分的影响。

2、FM提升了模型预估能力

依然看上面的示例，样本中没有<男性，化妆品>交叉特征，即没有男性看化妆品广告的数据。如果用多项式模型来建模，对应的交叉项参数$w_{\text{男性,化妆品}}$是学不出来的，因为数据中没有对应的共现交叉特征。那么多项式模型就不能对出现的男性看化妆品广告场景给出准确地预估。

FM模型是否能得到交叉项参数$w_{\text{男性,化妆品}}$呢？答案是肯定的。由于FM模型是把交叉项参数用对应的特征隐向量内积表示，这里表示为$w_{\text{男性,化妆品}}=⟨{\mathbf{v}}_{男性},{\mathbf{v}}_{化妆品}⟩$。

由于FM学习的参数就是单特征的隐向量，那么男性看化妆品广告的预估结果可以用$⟨{\mathbf{v}}_{男性},{\mathbf{v}}_{化妆品}⟩$得到。这样，即便训练集中没有出现男性看化妆品广告的样本，FM模型仍然可以用来预估，提升了预估能力。

3、 FM提升了参数学习效率

这个显而易见，参数个数由$(n^2+n+1)$变为$(nk+n+1)$个，模型训练复杂度也由$O(m{n}^2)$变为$O(mnk)$。$m$为训练样本数。对于训练样本和特征数而言，都是线性复杂度。

此外，就FM模型本身而言，它是在多项式模型基础上对参数的计算做了调整，因此也有人把FM模型称为多项式的广义线性模型，也是恰如其分的。

从交互项的角度看，FM仅仅是一个可以表示特征之间交互关系的函数表达式，可以推广到更高阶形式，即将多个互异特征分量之间的关联信息考虑进来。例如在广告业务场景中，如果考虑User-Ad-Context三个维度特征之间的关系，在FM模型中对应的degree为3。

最后一句话总结，FM最大特点和优势：

FM模型对稀疏数据有更好的学习能力，通过交互项可以学习特征之间的关联关系，并且保证了学习效率和预估能力。

五、实践

libfm实现了FM的基本操作，pyFM封装了libfm，因此在这里，我们用pyFM来实践一下FM算法。

pyFM官方github。pyFM在windows 10下的安装方法。

github的例子如下：

import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from pyfm import pylibfm
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
import  scipy.sparse
from sklearn.metrics import accuracy_score

X, y = make_classification(n_samples=1000,n_features=100, n_clusters_per_class=1)  # 1000个样本，100个特征，默认2分类

# 直接转化为稀疏矩阵，对有标称属性的数据集不能处理。
# X = scipy.sparse.csr_matrix(X)
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)

# 由于大部分情况下，数据特征都是标称属性，所以需要先转化为字典，再转化稀疏矩阵。（转化为系数矩阵的过程中标称数据自动one-hot编码，数值属性保留）
data = [ {v: k for k, v in dict(zip(i, range(len(i)))).items()}  for i in X]  # 对每个样本转化为一个字典，key为特征索引（0-99），value为特征取值
X_train, X_test, y_train, y_test = train_test_split(data, y, test_size=0.1, random_state=42)

v = DictVectorizer()
X_train = v.fit_transform(X_train)  # 转化为稀疏矩阵的形式，fm算法只能是被这种格式
X_test = v.transform(X_test)  # 转化为稀疏矩阵的形式，fm算法只能是被这种格式
# print(X_train.toarray())   # 打印二维矩阵形式

# 建模、训练、预测、评估
fm = pylibfm.FM(num_factors=50, num_iter=300, verbose=True, task="classification", initial_learning_rate=0.0001, learning_rate_schedule="optimal")
fm.fit(X_train,y_train)
y_pred_pro = fm.predict(X_test)  # 预测正样本概率
for i in range(len(y_pred_pro)):
    if y_pred_pro[i]>0.5:
        y_pred_pro[i] = 1
    else:
        y_pred_pro[i] = 0
print("fm算法 验证集log损失: %.4f" % accuracy_score(y_test,y_pred_pro))


lr = LogisticRegression(verbose=True)
lr.fit(X_train,y_train)
y_pred_pro = lr.predict(X_test)  # 预测正样本概率
print("逻辑回归 验证集log损失: %.4f" % accuracy_score(y_test,y_pred_pro))

'''
fm算法 验证集log损失: 0.7000
[LibLinear]逻辑回归 验证集log损失: 0.8800
'''

我们发现，代码跑得很慢，并且精度也很差。因此，一个新的封装了FM和FFM的工具包xLearn应运而生。
xlearn的优势：
1.通用性好，包括主流的算法（lr, fm, ffm 等），用户不用再切换于不同软件之间
2.性能好,测试 xLearn 可以比 libfm 快13倍，比 libffm 和 liblinear 快5倍
3.易用性和灵活性，xLearn 提供简单的 python 接口，并且集合了机器学习比赛中许多有用的功能
4.可扩展性好。xLearn 提供 out-of-core 计算，利用外存计算可以在单机处理 1TB 数据

可惜得是，目前xLearn只支持Linux和Mac，Windows用户可能要等等了。因为条件的原因，等着xLearn开放了Windows的接口后，我再补上内容。

参考文献

【1】第09章：深入浅出ML之Factorization家族
【2】深入FFM原理与实践
【3】CTR预估算法之FM, FFM, DeepFM及实践
【4】python机器学习案例系列教程——CTR/CVR中的FM、FFM算法
【5】Rendle, S. (2010, December). Factorization machines. In Data Mining (ICDM), 2010 IEEE 10th International Conference on (pp. 995-1000). IEEE.
【6】一文读懂FM算法优势，并用python实现！（附代码）