SIR及SEIR建模的简单示例

概述

看了一些2019-nCoV相关的文章，摘录并总结了一些关于SIR和SEIR模型的定义。并通过代码进了简单模型的实现，使用R语言作为编程工具。

1.一些定义

1.1 一些名词

序号	词汇	解释
1	Pneumonia	肺炎
2	Coronavirus	冠状病毒
3	Incubation	潜伏
4	Quarantined	隔离
5	Susceptible	易感的，这里用于指易感人群，在CDC的公告中，所有人都属于易感人群。
6	zoonotic	动物传播的
7	Reproductive	再生，复制。这里指感染者再传播并产生新的感染者。
8	novel	新的
9	2019-nCoV	2019新型冠状病毒

1.2 一些符号

序号	符号	含义
1	$R_0$	基础再传播人数
2	$\tau$	传染概率，一名易感者和一名感染者接触时被感染的概率
3	$\bar{c}$	单位时间内和感染者接触的易感人员的平均比例值
4	$d$	感染暴露时长
5	$S$	易感人群
6	$I$	感染人群
7	$R$	移除人群，是指，被隔离或治愈而消除影响的感染人群
8	E	暴露人群, 处于潜伏期

1.3 一些定义

$$R_0=\tau \cdot \bar{c}\cdot d$$

用1小时表示1单位时长，通俗的理解：
$$再传播人数=传染率\cdot 接触易感人数的平均值\cdot 感染暴露时长$$
假定$\tau =0.2,\bar{c}=5,d=4$，则$R_0=4$

2.方法论

2.1 SIR

SIR(Susceptible-Infected-Removed)模型，用于传染病的传播人数进行建模。

关于模型的一些定义和假设：

1. N，封闭系统内的总人口。
2. 传染率、排除率等为常量。
3. 不考虑出生和自然死亡。
4. 人群是均匀混合的。任何感染者可以以概率接触任何一名易感者，这里的概率可以用总体均值来替代。

通过模型的假设我们可以看到，SIR实际上是对传染病流行早期传播行为的建模。模型形式如下：
$$\{\begin{array}{rl}& \frac{ds}{dt}=-\beta si\\ & \frac{di}{dt}=\beta si-\gamma i\\ & \frac{dr}{dt}=\gamma i\end{array}$$
其中$\beta =\tau \bar{c}$表示有效接触率，$v$表示消除率， $\gamma $表示移除率，都是常量。因而传染暴露时长实际上是$v$的倒数，有$d=\gamma^{-1}$。

当传染病爆发时，感染者人数随着时间上升，因此有$di/dt\ge 0$，从而有：
$$\begin{gathered} \beta si-\gamma i> \\ \frac{\beta si}{\gamma }>i \end{gathered}$$
在一场疫情的爆发之初，每个人都可视为易感染群，因此这里$s\approx 1$，代入上式有：
$$\frac{\beta }{\gamma }=\tau \bar{c}d=R_0>1$$
因而当$R_0>1$时疫情是处于传染阶段的。

对上述微分方程组求解得到：
$$I=(S_0+I_0)-S+\frac{1}{R_0}\ln \frac{S}{S_0}$$
其中$S_0,I_0$表示初值。当$S_0<\frac{1}{R_0}$时传染降低，为了达到这个目的可采取以下措施：

1. 降低$S_0$,即减少易感者数量，在这里也就是戴口罩、不外出等。
2. 提高$\frac{1}{R_0}$,即降低$\beta $(接触率)，在这里也就是减少人员流动。
3. 提高$\gamma$(移除率)，提高隔离率或治愈率。

2.2 SEIR

SEIR(Susceptible-Exposed-Infected-Removed)，类似于SIR，但是增加了对潜伏期的定义，因此更适用于具有一定潜伏期的传染病。状态之间的转化如下所示：

其中，$\lambda$表示易感人群的输入(人口增加)，$\mu$表示死亡率，$k$表示从暴露人群到确诊感染者的比率，$\gamma$是感染者的移除率。模型由如下四个等式组成：
$$\begin{array}{rl}\dot{S}& =-\beta SI+\lambda -\mu S\\ \dot{E}& =\beta SI-(\mu +k)E\\ \dot{I}& =kE-(\gamma +\mu )I\\ \dot{R}& =\gamma I-\mu R\end{array}$$

2.3 代际传播

2.3.1 传播矩阵

对于同一种传染病而言，每一个患者的感染途径可能是不同的，比如：蝙蝠传人、男人传女人、狗传人等。定义代际传播矩阵$\mathbf{G}$，其中元素$g_{i,j}$表示下一代中由一个$j$类病患导致的$i$类病患的数量，由此可知$\mathbf{G}$是方阵。同时$R_0$对应$G$的谱半径（绝对值最大的特征值）。从$\mathbf{G}$的数学性质来看，它是非奇异的，同时具有一个正的特征值并且严格大于其它特征值，实际上这个特征值就是$R_0$。

对于只有两种状态的传染病而言有：
$$\mathbf{G}=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]$$
其特征值为：${\lambda }_{\pm }=\frac{a+d}{2}\pm \sqrt{((a+d)/2{)}^2-(ad-bc)}$

此外，$\mathbf{G}$也可以写成入下形式：
$$\mathbf{G}=F{V}^{-1}$$
其中$F=\left[\frac{\partial F_i(x_0)}{\partial x_j}\right]$表示新增感染者，$V=\left[\frac{\partial V_i(x_0)}{\partial x_j}\right]$表示感染者的区间传播。

3 模型实现

编码采用R语言，对于SIR系列的建模，R语言中有现成的软件包：SimInf。为了展示数据的迭代过程，这里并不打算直接采用。

3.1 参数设定

结合当前实际情况，有如下设定：

• N，以武汉为中心的辐射人口：19 000 000。
• $\mu$, 患病死亡率：0.02。
• $I_0$，期初患病人数：1。
• $\frac{\beta }{\gamma }$， 2.68。

3.2 SIR

library(deSolve) 
library(ggplot2)

（1）模型

基于如下微分方程组构建模型
$$\begin{array}{rl}& \frac{ds}{dt}=-\beta si\\ & \frac{di}{dt}=\beta si-\gamma i\\ & \frac{dr}{dt}=\gamma i\end{array}$$

sir <- function(time, state, pars) {
  with(as.list(c(state, pars)), {
    dS <- -beta * S * I/N
    dI <- beta * S * I/N - gamma * I
    dR <- gamma * I
    return(list(c(dS, dI, dR)))
  })
}

（2）参数

N <- 1.9e8 # 总人口
I0 <- 1 # 初始感染者数量
RM0 <- 0 # 初始移除人员数量
S0 <- N - I0 - RM0 # 初始易感人群数量
init <- c(S = S0, I = I0, R = RM0) # 初始值
# 以下参数在模型假定下是常量
pars <- c(
  beta = 0.55, # 有效接触率
  gamma = 0.2, # 移除率
  N = N # 人口
  ) 
# 迭代次数，以天计
times <- seq(0, 150, by = 1) 

（3）计算

res <- as.data.frame(ode(y = init, times = times, func = sir, parms = pars))

（4）绘图

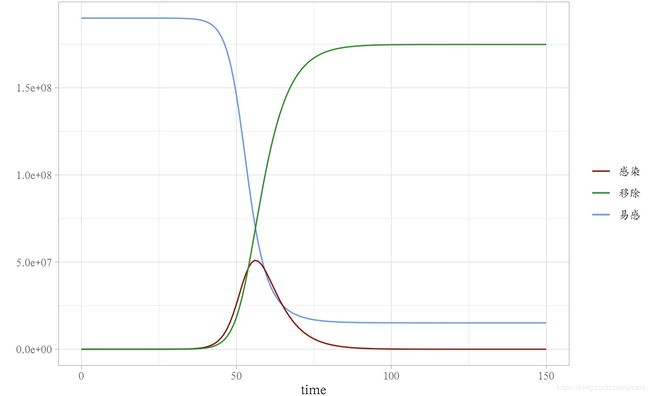
ggplot(res) +
  geom_line(aes(x = time, y = S, col = '易感'))+
  geom_line(aes(x = time, y = I, col = '感染'))+
  geom_line(aes(x = time, y = R, col = '移除'))+
  theme_light(base_family = 'Kai') +
  scale_colour_manual("",
  values=c("易感" = "cornflowerblue", "感染" = "darkred", "移除" = "forestgreen")
  ) +
  scale_y_continuous('')

3.3 SEIR

（1）模型

基于如下微分方程组构建模型
$$\begin{array}{rl}\frac{ds}{dt}& =-\beta S\frac{I}{N}\\ \frac{de}{dt}& =\beta S\frac{I}{N}-kE\\ \frac{dI}{dt}& =kE-(\gamma +\mu )I\\ \frac{R}{dt}& =\gamma I\end{array}$$

seir<-function(time, state, pars){ 
  with(as.list(c(state, pars)),{ 
    dS <-- S * beta * I/N 
    dE <- S * beta * I/N - E * k 
    dI <- E * k - I * (mu + gamma) 
    dR <- I * gamma
    dN <- dS + dE + dI + dR 
    
    list(c(dS,dE,dI,dR,dN)) 
  }) 
} 

（2）参数

N <- 1.9E8 # 总人口
I0 <- 89 # 期初感染数
E0 <- 0 # 期初潜伏数
RM0 <- 0 # 期初移除数
S0 = N - I0 - RM0 # 期初易感人数
init<-c(S = S0, E = E0, I = I0, R = RM0, N = N)	
time <- seq(0, 150, 1) 
pars<-c( 
  beta = 0.55,	#有效接触率
  k = 1,	#潜伏到感染的转化率 
  gamma = 0.2,	#RECOVERY 
  mu=0.02	#感染期死亡率 
) 

（3）计算

res.seir<-as.data.frame(lsoda(y = init, times = time, func = seir, parms = pars)) 

（4）绘图

ggplot(res.seir) +
  geom_line(aes(x = time, y = S, col = '2 易感'))+
  geom_line(aes(x = time, y = E, col = '3 潜伏'))+
  geom_line(aes(x = time, y = I, col = '4 感染'))+
  geom_line(aes(x = time, y = R, col = '5 移除'))+
  geom_line(aes(x = time, y = N, col = '1 人口'))+
  theme_light(base_family = 'Kai') +
  scale_colour_manual("",
  values=c(
    "2 易感" = "cornflowerblue", "3 潜伏" = "orange",
    "4 感染" = "darkred", "5 移除" = "forestgreen", 
    "1 人口" = "black"
    )
  ) +
  scale_y_continuous('')

3.4 小结

对比SIR和SEIR模型的结果，可以看到，相同条件下具有潜伏期的疾病其感染人数峰值的到来要晚于没有潜伏期的疾病，并且持续时间更长。

参考文献

1. Joseph T Wu*, Kathy Leung*, Gabriel M Leung. Nowcasting and forecasting the potential domestic and
   international spread of the 2019-nCoV outbreak originating
   in Wuhan, China: a modelling study.Lancet,2020.
2. Gerardo Chowell.Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts.Infectious Disease Modelling,2017.
3. James Holland Jones.Notes On R0.2007.