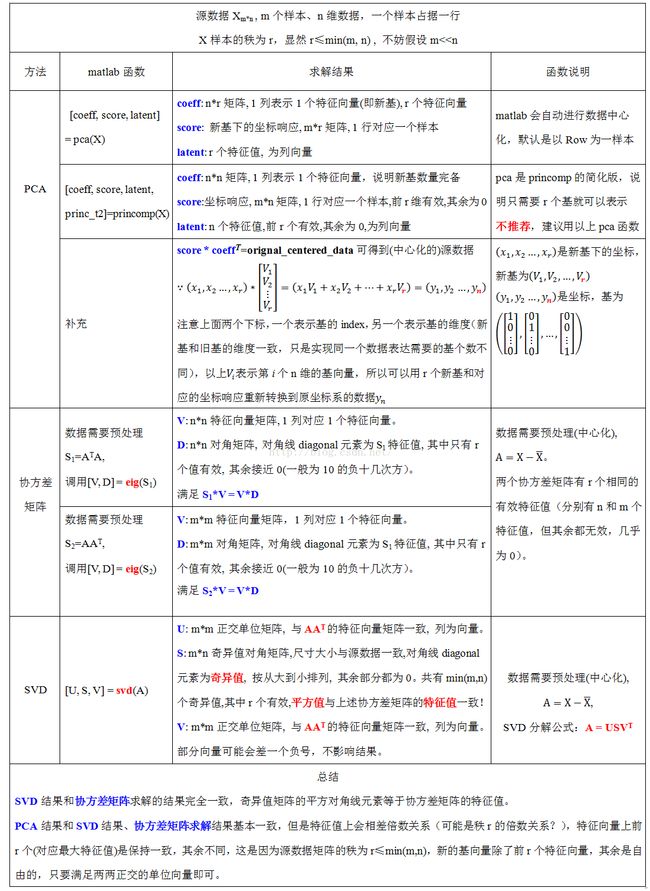
PCA、SVD、协方差矩阵求解的关系和对比(例子说明)
基本上看下面这个图就知道了,如果想要验证,可以接着看下面的数据计算实例。
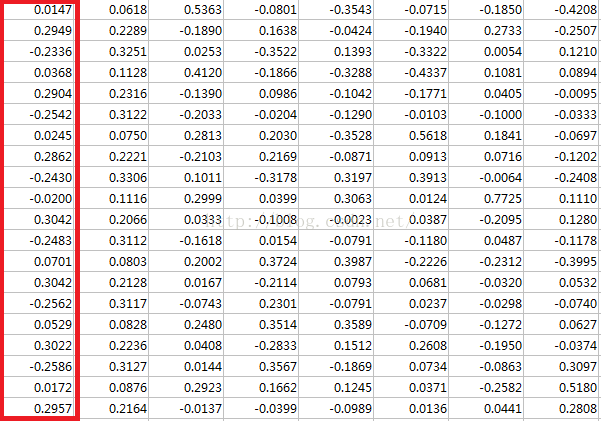
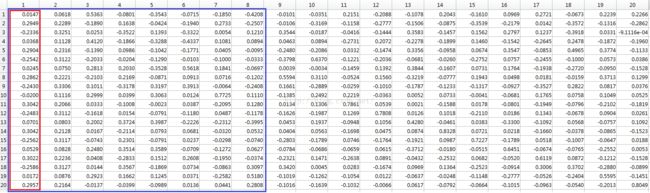
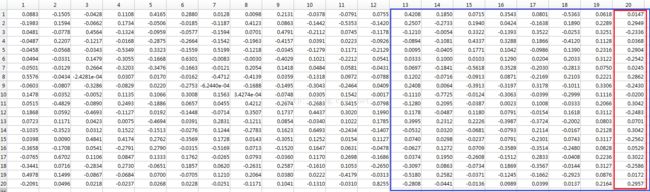
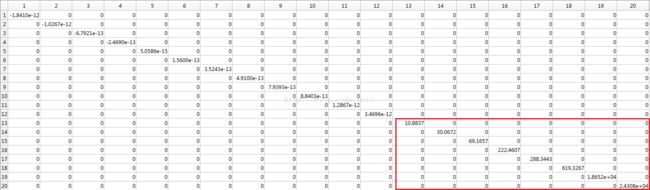
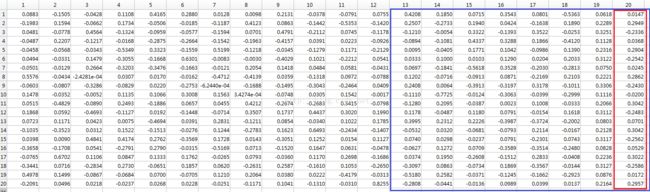
源数据X: 9*20, 9个样本, 20维
源数据
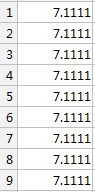
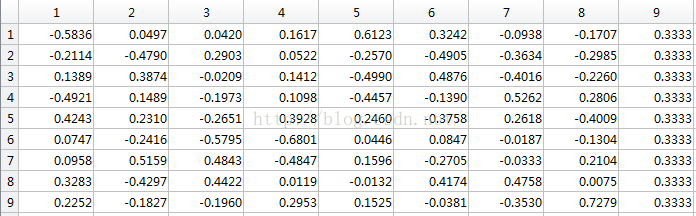
平均值
![]()
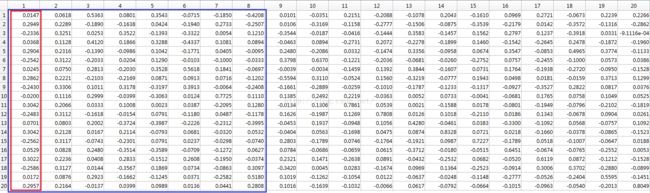
数据中心化:
PCA方法求解
[PCA_coeff, PCA_score, PCA_latent] =pca(X) //默认一行为一个数据样本,matlab自动进行数据中心化
PCA_coeff :主成分向量,每一列是一个成分,对应一个基向量
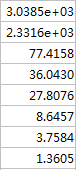
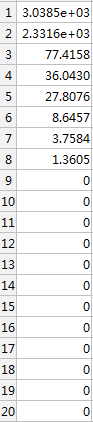
PCA_latent:特征值
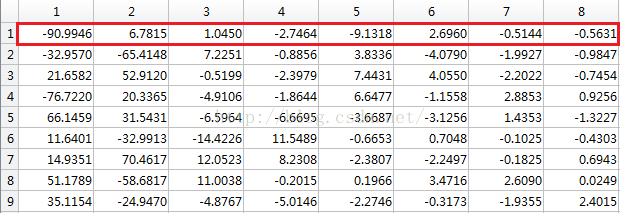
PCA_score: 新基下的坐标响应
PCA分解
[princ_coef, princ_score, princ_latent,princ_t2] = princomp(X)
help('princomp')
princomp Principal Components Analysis(PCA).
Using princomp is discouraged. Use PCA instead. Calls to princomp are
routed to PCA. Please see the documentation of PCA for help.
[coeff, score, latent, tsquare] = princomp(x,econFlag)
princ_coeff:一列为基向量,和PCA一致,只是多了不必要的基向量,但这基向量完备!
(以下是用X'*X做出的特征向量矩阵,有8个特征向量是一致的,只是差了一个负号,由于源数据样本的秩为8,所以转换后主成分基只需要8个,就能够表达源数据,而其余的基只要正交即可,所以剩余的不同。)
princ_latent:特征值
princ_score: 9个样本,每个样本一行,一行每个分量是新基上的响应(就是坐标值,是新坐标系下的值)
princ_t2
用协方差矩阵求解特征值
[Va, Da] = eig(X'*X) [Vb, Db] = eig(X*X')
[V,D] = eig(X) produces a diagonal matrix D of eigenvalues and a
full matrix V whose columns are the corresponding eigenvectors so
that X*V = V*D.
[V,D] = eig(X,'nobalance') performs the computation with balancing
disabled, which sometimes gives more accurate results for certain
problems with unusual scaling. If X is symmetric, eig(X,'nobalance')
is ignored since X is already balanced.
直接对 X 进行求解,发现两个特征值一模一样eig(X'*X)==eig(X*X'),但是对应的特征向量不一样
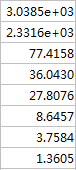
Da对应特征值:
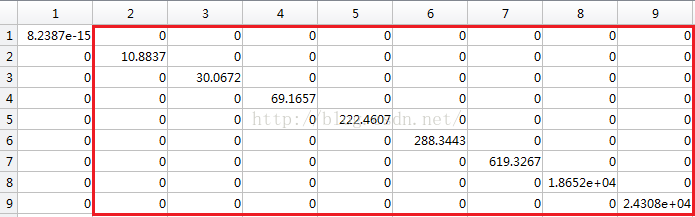
Db:X'*X 特征值
和PCA做出来的特征差倍数关系(倍数=8=特征值个数)
(以下是用SVD做出的奇异值的平方,发现与X'*X 特征值一致)
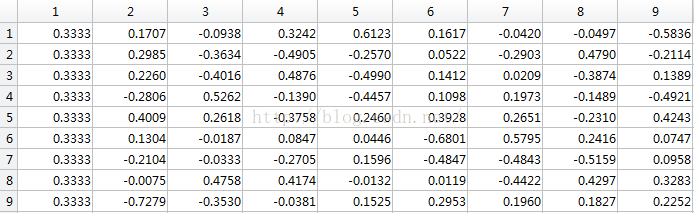
Va:X*X' 特征向量,一列为一个特征向量
Vb:特征向量,一列为一个特征向量
SVD分解
[svd_U, svd_S, svd_V] = svd(X)
[U,S,V] = svd(X) produces a diagonal matrix S,of the same
dimension as X and with nonnegative diagonal elements in
decreasing order, and unitary matrices U and V so that
X= U*S*V'.
[U,S,V] = svd(X,0) produces the "economysize"
decomposition. If X is m-by-n with m > n, then only the
first n columns of U are computed and S is n-by-n.
For m <= n, svd(X,0) is equivalent to svd(X).
[U,S,V] = svd(X,'econ') also produces the"economy size"
decomposition. If X is m-by-n with m >= n, then it is
equivalent to svd(X,0). For m < n, only the first m columns
of V are computed and S is m-by-m.
svd_S:奇异值
svd_S2 = svd_S.^2
svd_U: 和X*X' 特征向量保持一致,区别就是排序不一样
svd_V:和X*X' 特征向量保持一致(部分向量差一个负号,不影响结果)