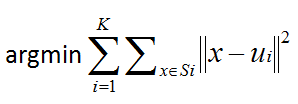聚类算法--K-Means（基于R的应用示例）

K-Means算法描述

前文http://blog.csdn.net/buracag_mc/article/details/74025510已经定义好了对象之间距离的测度。在确定了距离定义下，K-Means聚类算法要求事先确定聚类数目K，并采用分隔方式事先聚类。所谓分隔是指:

首先，将样本随机分成K个区域，对应K个类，并确定K个类的质心位置（一般是指定初始质心的位置）；

然后，计算各个观测点与K个质心的距离，将所有观测点指派到与之最近的类中，形成初始的聚类结果；

由于初始聚类结果是在空间随意分隔的基础上产生的，无法确保所得到的K个类就是客观存在的“自然小类”，故需多次执行，直到收敛或达到终止条件。

 

所以，K-Means聚类算法的具体过程如下：

第一步，输入聚类数目K和待分类数据集。在K-Means聚类中，要根据最终的聚类效果，实际选取K值。

 

第二步，确定K个初始类质心。初始类质心指定的合理性将直接影响到聚类算法收敛的速度。常见的初始类质心的指定方法有：
1.经验选择法，即根据以往经验大致了解聚类数目；

2.随机选取法，即随机指定K个样本观测点作为初始类质心；

3.最小最大法，即先选择所有观测点中相距最远的两个点作为初始类质心，然后选择第三个观测点，它与已确定的类质心的聚类是其余点中最大的。然后按照同样的原则选择其他类质心。

 

第三步，根据最近原则进行聚类。计算样本点到K个类质心的聚类，并按照距K个类质心距离最近的原则，将所有观测分派到最近的类中，形成K个类。

 

第四步，重新确定K个类质心。重新计算K个类的质心（类中各观测点均值），并以该均值点作为新的类质心。

 

第五步，重复三、四步，判断是否达到收敛条件或最大迭代次数。

 

其实，原理很简单。K-Means聚类过程本质上是一个优化求解过程。记样本中的n个观测数据为，K个类记为，则K-Means聚类就是要找到类内离差平方和最小下的类，即

其中ui是第Si类的质心。

 

从而可以知道以下统计量：

##对观测全体计算p个聚类变量的离差平方和之和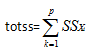：，SSXi表示聚类变量Xi的离差平方和。totss是对全体观测离散总程度的测度。

 

##对最终得到的每个小类，计算p个聚类变量离差平方和之和，并加总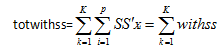：,表示聚类变量Xi的类内离差平方和。totwithss可作为类内离散总程度的测度。

 

##计算betweenss = totss-totwithss，它可作为类间离散总程度的测度。

 

所以，在聚类数目K确定的条件下，totwithss越小越好（类内相似度高）。另外，还需考虑betweenss越大越好（类间差异性性大），也即betweenss/totwithss越大越好。进一步，为消除聚类数目K和样本量n对计算结果的影响，可将betweenss/totwithss修正为：(betweenss/(K-1))/(totwithss/(n-K))，也即此值越大越好。

 

基于R的应用示例

 

函数简述

K-Means聚类的R函数命令是kmeans，基本命令如下：

Kmeans(x=数据矩阵， centers=聚类数目或初始聚类质心，iter.max=10，nstart=1)

 

其中：

1.待聚类样本组织在x指定的矩阵或数据框中。

2.参数centers：若为一个整数，则表示聚类数目K；若为一个矩阵（行数等于聚类数目K，列数等于聚类变量个数），则表示初始类质心，每一行表示一个初始类质心。

3.参数iter.max用于指定最大迭代次数，默认为10次。R中仅以最大迭代次数作为终止迭代条件。

4.当参数为centers为一个整数时，R将采用随机选择法从数据中抽取K个观测值作为初始类质心。我们，不同的初始类质心对最终的聚类结果是存在影响的。所以，R为克服大数据集下终止迭代次数不充分大时，初始类质心抽取的随机性对聚类结果的影响，可指定参数nstar为一个大于1的值（默认为1），表示重复多次抽取质心。

 

Kmeans函数的返回结果是一个列表，包括如下成分：

1.cluster：存储各观测所属的类别编号，也称聚类解。

2.centers：存储各个类的最终类质心。

3.totss：所有聚类变量的离差平方和之和，是对类内部观测数据点离散程度的测度。

4.cotwithss：每个类内所有聚类变量的离差平方和之和的总和。

5.betweenss：各类别间的聚类变量离差平方和之和

6.size：各类的样本量。

 

应用示例

模拟步骤如下：

1.首先，生成包含50个观测且包含2个“最小自然类”的随机样本。

 

2.然后，利用K-Means将样本数据聚成2类。

 

(KMClu1<-kmeans(x=x,centers=2,nstart=1))  

plot(x,col=(KMClu1$cluster+1),main="K-Means聚类K=2",xlab="",ylab="",pch=20,cex=1.5)

 

 

3.利用K-Means将样本数据聚成4类。通过对比2类和4类下的(between/K-1) / (totwithss/n-K),发现聚成4类不恰当。

 

KMClu2<-kmeans(x=x,centers=4,nstart=1)   

plot(x,col=(KMClu2$cluster+1),main="K-Mean聚类K=4,nstart=1",xlab="",ylab="",pch=20,cex=1.5)

 

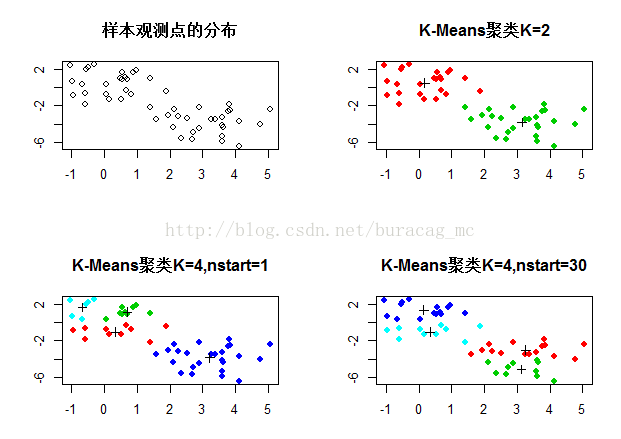
发现聚成4类是不恰当的：

 

 

最后，附上完整代码和样例图：
###对模拟数据的K-Means聚类###

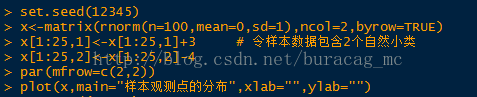
set.seed(12345)

x<-matrix(rnorm(n=100,mean=0,sd=1),ncol=2,byrow=TRUE)  

x[1:25,1]<-x[1:25,1]+3     # 令样本数据包含2个自然小类      

x[1:25,2]<-x[1:25,2]-4

par(mfrow=c(2,2))

plot(x,main="样本观测点的分布",xlab="",ylab="")  

 

###将样本聚成2类###

set.seed(12345)

(KMClu1<-kmeans(x=x,centers=2,nstart=1))  

plot(x,col=(KMClu1$cluster+1),main="K-Means聚类K=2",xlab="",ylab="",pch=20,cex=1.5)

points(KMClu1$centers,pch=3)

 

###将样本聚成4类，其中nstart=1###

set.seed(12345)

KMClu2<-kmeans(x=x,centers=4,nstart=1)   

plot(x,col=(KMClu2$cluster+1),main="K-Means聚类K=4,nstart=1",xlab="",ylab="",pch=20,cex=1.5)

points(KMClu2$centers,pch=3)

KMClu1$betweenss/(2-1)/KMClu1$tot.withinss/(50-2)

KMClu2$betweenss/(4-1)/KMClu2$tot.withinss/(50-4)

 

###将样本聚成4类，其中nstart=30###

set.seed(12345)

KMClu2<-kmeans(x=x,centers=4,nstart=30)

plot(x,col=(KMClu2$cluster+1),main="K-Means聚类K=4,nstart=30",xlab="",ylab="",pch=20,cex=1.5)

points(KMClu2$centers,pch=3)

 

###########样例图###########