【原创】2019.10.12模拟赛 NP问题 坏天平

2019.10.12模拟赛

说在前面

四年前，小白甜；
四年后，腹黑透。

orz NODGD。

NP问题

问题描述

p6pou在平面上画了$n$个点，并提出了一个问题，称为$N-Points$问题，简称NP问题。
p6pou首先在建立的平面直角坐标系，并标出了这$n$个点的坐标。这 个点的坐标都是正整数，任意三个点都不共线。然后，p6pou选择其中一个点$A$ ，画一条$y$轴的平行线，这条直线称为$l$。直线$l$以点$A$为旋转中心逆时针旋转，当直线$l$碰到另外一个点$B$时，就立刻将$B$点作为新的旋转中心继续逆时针旋转。此后，每当直线$l$碰到除了旋转中心以外的另一个点，都会将这个点作为新的旋转中心继续逆时针旋转。这个过程可以一直进行。
p6pou不太关心旋转的完整过程，只想知道，当 旋转至平行于 轴时直线方程有哪些可能。

输入格式

输出文件$np.in$。
第一行输入两个整数$n,A$，表示平面上共有$n$ 个点，一开始$l$与$y$轴平行，直线方程是$x=A$。
第$1$到第$n$行中，第$i$行两个正整数$x_i,y_i$，表示编号为$i$的点的坐标，保证任意三点不共线。

输出格式

输出文件$np.out$。
直线$l$旋转到与$x$轴平行时方程是$y=B$，按从小到大的顺序输出$B$所有可能的值，每行输出一个数。

输入输出样例1

样例输入

4 1
1 2
2 1
3 2
2 3

样例输出

1
3

样例说明

输入输出样例2

样例输入

6 2
2 2
2 4
4 1
4 2
3 4
1 3

样例输出

2
3
4

样例说明

数据规模与约定

对于100%的数据，n<=200 。

分析

这个包里三个700MB的视频，2个G的样例包，差点没吓死我。
于是我录了个gif挂在上面了。

我的做法啊……

以上是考场分析。

因为我相信数学是美丽而优雅的，所以我只dfs了两圈，就是从A点出发以后，第二次回来的话就结束程序。
于是就90分了。
如果我跑4圈就能A。
最好跑n圈，反正时间复杂度够，n才两百。
所以为什么n才两百呢？

于是我寻思着你造数据的时候就造一个大圆大椭圆大抛物线，在上面取点呗，你题面不写保证所有点在一个圆上，也没人会针对你的数据投机取巧，也不至于水到哪里去。

还是那句话，不喜欢冠冕堂皇以暴力为正解的题目。

所以简单说几句正解。为什么说$l$两边的点的个数不变呢？
因为你旋转的时候，撞到了一个点。假设在撞之前，左边有L个，右边有R个，线上只有1个是我原来的旋转中心A，而我新撞到的点是点B，假设A在B左边，那么在撞到你B的前一瞬间，你B在我右边，你现在到线上了，R–，但我A出来了，而且我A不仅出来了还在你l的右边（画图自己看），所以R++。什么也没有发生。

所以我开始竖着的时候的L,R和我在任意时刻的L,R是不会变的。
而可能出现的横着的l就那么n个。
所以排排序就解决了。

#include
#include
#include
#include
#include
using namespace std;
 
inline void Read(int &p)
{
    p=0;
    char c=getchar();
    while(c<'0' || c>'9') c=getchar();
    while(c>='0' && c<='9')
        p=p*10+c-'0',c=getchar();
}
 
const int MAXN=444;
const double pi=acos(-1.0);
 
struct node
{
    int id;
    double alpha;
    bool operator < (const node &n) const
    {
        return alpha<n.alpha;
    }
}arr[MAXN][MAXN];
int n,A,c,B[MAXN],x[MAXN],y[MAXN],ok[MAXN],cnt[MAXN],ans[MAXN];
 
double angel(int i,int j)
{
    double ans=(x[i]==x[j])?pi/2.0:atan((1.0*y[i]-y[j])/(x[i]-x[j]));
    if(ans<0) ans+=pi;
    return ans;
}
 
void dfs(int now,int las,int ed,int all)
{
    if(now==ed) all++;
    if(all==n) return ;
    int pos=(upper_bound(arr[now]+1,arr[now]+1+cnt[now],(node){now,angel(now,las)})-arr[now]);
    if(arr[now][pos].alpha>=pi) ok[now]=1;
    dfs(arr[now][pos].id,now,ed,all);
}
 
int main()
{
    Read(n),Read(A);
    for(int i=1;i<=n;i++) Read(x[i]),Read(y[i]);
    for(int i=1;i<=n;i++)
    {
        if(x[i]==A) B[++c]=i;
        for(int j=1;j<=n;j++)
            if(i!=j)
            {
                arr[i][++cnt[i]].id=j,arr[i][cnt[i]].alpha=angel(i,j);
                if(arr[i][cnt[i]].alpha<pi) arr[i][++cnt[i]].id=j,arr[i][cnt[i]].alpha=arr[i][cnt[i]-1].alpha+pi;
            }
        sort(arr[i]+1,arr[i]+1+cnt[i]);
    }
 
    for(int i=1;i<=c;i++) dfs(B[i],B[i],B[i],0);
         
    for(int i=1;i<=n;i++) if(ok[i]) ans[++ans[0]]=y[i];
    sort(ans+1,ans+1+ans[0]);
    int las=ans[1]; printf("%d\n",las);
    for(int i=2;i<=ans[0];i++) if(ans[i]!=las) printf("%d\n",ans[i]),las=ans[i];
}

坏天平

分析

我们做的是题面5.0的，以下是题面4.0的内容。

题面5.0就直接告诉我们m没有任何用了。

我在考场上做了什么呢？

我做的事情就是算n=1的时候的答案。
题目残酷地告诉我，你辛苦求的$f[i]$居然是$C_i^{\lfloor \frac{i}{2}\rfloor }$。

---

先说说我的f[i]是在搞什么。
首先跳过无数错误的尝试。

$g(x,y)$代表左边放x个，右边放y个的方案数，显然$g(x,y)=g(x,y-1)+[x-1>=y]\ast g(x-1,y)$。然后$f[n]={\sum }_{i=1}^{\lfloor \frac{n+1}{2}\rfloor }g(i,n-i+1)$
所以我说这是一个畸形的杨辉三角：

于是我就愉快地得出了$f[n]$的前面几十项。
于是愉快的发现了规律$f[2n]=2\times f[2n-1],f[2n+1]=2\times f[2n]-Catalan(n)$。

---

我的式子的正确性不浪费时间讨论了，问题是题解给的$C_i^{\lfloor \frac{i}{2}\rfloor }$是怎么来的。

回到——$g(x,y)代表左边放x个，右边放y个的方案数，g(x,y)=g(x,y-1)+[x-1>=y]\ast g(x-1,y)$。然后$f[n]={\sum }_{i=\frac{n+1}{2}}^{n}g(i,n-i+1)$——这一步。

假设没有这个左比右大的条件，我们的答案可以在图上表示为（请忽略橙色的线）：

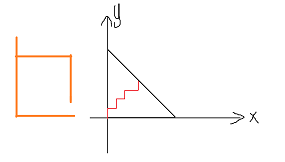
就是我们从$(0,0)$出发，每次横坐标或纵坐标$+1$，最后到达$x+y=n$这条线上某点的方案数，到达$(x_0,y_0)$就是这个点的方案数（就是我$C_n^{x_0}=C_n^{y_0}$哒，至于为什么？快用杨辉三角。你也可以这么理解，总共2n步，你从中选出n步填上向右/上走），然后把这些点全加起来就能得到$2^n$，这就是每一步从$x+1ory+1$中乱选一个的方案数。（这也许可以拿来证明二项式定理？）

那么本题的这个“左>=右”即“x>=y”的条件在图上怎么表现？它就是在说，你在走路的时候，不能越过$y=x$这个蓝线，也就是说，图中的红色是不合法的了，而绿色是合法的。

这是什么，这有卡特兰数内味了。

---

我们卡特兰数是怎么做的？

我们要从$(0,0)$走到$(n,n)$，而且走的时候不能超过$y=x$这条线，问方案数。
我们知道，不设要求乱走，我们的方案数是$C_{2n}^n$这么多，但加上了要求，要减去一些不合法的方案。不合法是什么意思？就是它超出了$y=x$，就是它走到了$y=x+1$上。

我们把不合法路径在越过$y=x$，来到$y=x+1$之后的路径关于$y=x+1$对称，容易发现，求终点为$(\mathbf{n},\mathbf{n})$，中途越过了$\mathbf{y}=\mathbf{x}$的方案数就等于终点为$(\mathbf{n}-1,\mathbf{n}+1)$，没有限制条件的方案数，即$C_{2n}^{n-1}=C_{2n}^{n+1}$。
所以就得到卡特兰数$Catalan(n)=C_{2n}^n-C_{2n}^{n-1}$，后续的化简就省略了。

---

那么对于本题的这个情况，它和卡特兰数的区别在哪里？
它同样有一条不可跨越的线$y=x$，同样从$(0,0)$出发——对了，终点不同，卡特兰数的终点是$(n,n)$，而它的终点则不止一个，$(n,n)$,$(n+1,n-1)$……$(2n,0)$。
终点是$(n,n)$的情况的方案数就是$Catalan(n)=C_{2n}^n-C_{2n}^{n+1}$，那么$(n+1,n-1)$呢？
如果不加限制，我们的方案数就是在一个长为$2n$的操作序列里面选$n+1/n-1$个格子填上向右走/向左走的方案数，就是$C_{2n}^{n+1}=C_{2n}^{n-1}$。
对于那些超过了线的，我们把它的从第一处超过线的位置开始的部分关于$y=x+1$对称，就得到一条从$(0,0)$自由自在无忧无虑走到$(n-2,n+2)$的路线。总共多少条呢，与上文类似的，$C_{2n}^{n-2}=C_{2n}^{n+2}$？
所以说终点为$(n+1,n-1)$的答案是$C_{2n}^{n-1}-C_{2n}^{n-2}$。
敏锐的读者、数学功底无限好的你们一定发现了顶好的规律，你把这些个终点的答案一加起来就得到了$f[2n]=C_{2n}^n-C_{2n}^0=C_{2n}^n$。

太棒了！现在我们知道n=1时的答案了，这样我们就得到了——零分！可喜可贺，可喜可贺。
（出题人，你好狠）

不过n>1的思路在我的那张便签里也有体现，本人，虽然智力障碍，但还是勇敢地试图递推！


以上是题解。

数学功底无限差的我还需要要绕一大圈才能明白，跟我一起绕圈圈吧。
它这个递推和常规的递推有些不同，我们（也许只有我）一般是考虑把第n种物品加入，然后由$d{p}_{n-1}$推出$d{p}_n$。这道题则是把最轻的砝码拿了出来。

现在我们求$an{s}_n$，我们假设我们没有$m^0$这种砝码，只用$m^1,m^2,\cdots ,m^{n-1}$这$n-1$种砝码能摆出的方案数是多少？$an{s}_{n-1}。$
现在我们把$m^0$插入这些方案中。因为它是最轻的，如果我们把$m^0$放在$m^1,m^2,\cdots ,m^{n-1}$之中，我们可以随便摆，爱咋摆咋摆。所以我们设有$i$个$m^0$摆在了大部队之前，它能贡献的方案数就是$C_i^{i/2}(整除)$。那么剩下$k-i$个呢？现在就是一个插板的经典问题了。这篇blog的T1就详细地解释了这个问题。 自己看去。

除去开头的一个，总共$k\ast (n-1)=k\ast n-k$个间隔。你要把$k-i$个板子插进去，而且每个间隔可以塞多个板子。
我们可以把这个的方案数看作方程$x_1+x_2+\cdots +x_{k-i}=k\ast n-k$的非负整数解的个数。
于是我们为了规避某个$x=0$,即某个间隔上出现了多个板子的情况出现，我们把所有$x++$，变成$x_1+x_2+\cdots +x_{k-i}=k\ast n-k+k-i=k\ast n-i$的正整数解的个数，在$k\ast n-i$个间隔里面选$k-i$个出来插板，这是什么啊，这是$C_{k\ast n-i}^{k-i}$。

每次插入时，你都可以任选放在左边还是右边，所以再乘上$2^{k-i}$。

然后枚举$i$。
然后递推推起来。
时间复杂度$\Theta (nk)$。

我的数学怎么这么差。

代码

#include
#include
#include
#include
#include
using namespace std;
 
inline void Read(int &p)
{
    p=0;
    char c=getchar();
    while(c<'0' || c>'9') c=getchar();
    while(c>='0' && c<='9')
        p=p*10+c-'0',c=getchar();
}
 
const int MAXN=10002030,mod=998244353;
int n,m,k,inv[MAXN],arkcpy[MAXN];
 
int main()
{
    inv[0]=inv[1]=arkcpy[0]=1;
    Read(n),Read(m),Read(k);
    for(int i=2;i<=k;i++) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
    for(int i=1;i<=k;i++) arkcpy[i]=1ll*arkcpy[i-1]*i%mod*inv[(i+1)>>1]%mod;
    long long ans=arkcpy[k];
    for(int i=2;i<=n;i++)
    {
        long long t=0,c=1;
        for(int j=0;j<=k;j++) (t+=1ll*c*arkcpy[k-j])%=mod,(c*=2ll*((i-1)*k+j)%mod*inv[j+1]%mod)%=mod; 
        (ans*=t)%=mod;
    }
    cout<<ans<<endl;
}

垃圾分类

这道题真的是垃圾分类，我被分出来了。我是有害垃圾，应当深挖掩埋焚烧隔离。
没想，没写，没打暴力，没看题解。

（其实我看了）