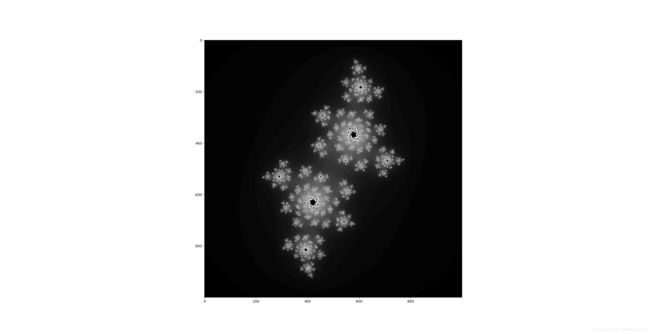
分形：MandelBrot和Julia

分形：MandelBrot和Julia

MandelBrot

• MandelBrot点是构造这样的一个集合：对于复平面上任意点z， x(0) = 0，使用公式x(n+1) = x(n)^2 + z迭代，若最终收敛，则属于此集合

Julia

• Julia集合如示例代码所述，复平面上的点作为x(0)，控制点z取任意值，得到不同的Julia点集

参考代码

• 如下，白色部分就是所求集合

import numpy as np

SEGS = 1000

data = np.zeros([SEGS, SEGS])

MAX_ABS = 1.7
xmin,xmax,ymin,ymax = (-MAX_ABS,MAX_ABS, -MAX_ABS,MAX_ABS)

JULIA_OR_MANDELBROT = True
JULIA_CONTROL_POINT = complex(-0.577, 0.511)

for i in range(SEGS):
    for j in range(SEGS):
        z = complex(xmin + (xmax - xmin) / (SEGS-1) * i, ymin + (ymax - ymin) / (SEGS-1) * j)
        x = complex()

        if JULIA_OR_MANDELBROT:
            x,z = z,x
            z = JULIA_CONTROL_POINT

        iter_cnt = 0
        while (x * x.conjugate()).real < 4:
            iter_cnt += 1
            x = x * x + z
            if iter_cnt > 64:
                break

        if abs(x) < 2:
            data[i][j] = 0
        else:
            data[i][j] = iter_cnt / 64


from matplotlib import pyplot as plt
plt.gray()
plt.imshow(data, interpolation='nearest')
plt.show()