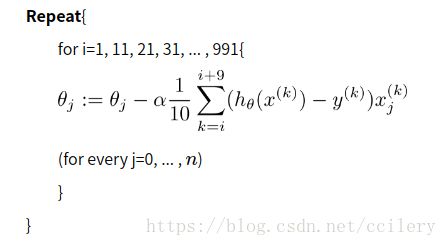线性回归——梯度下降法

统计学习方法主要包括三部分：模型、策略、算法。模型指的是确定一个由函数组成的集合，策略指的是定义对集合中函数的评价准则，算法则指的是从函数集合中按照定义的评价准则找到最优的函数的方法。

本部分从线性回归模型出发，以最小乘为评价准则，介绍梯度下降算法：批量梯度下降(Batch Gradient Descent, BGD)，随机梯度下降(Stochastic Gradient Descent, SGD) 小批量梯度下降(Mini-batch Gradient Descent, MBGD)

模型

线性回归(Linear Regression)的假设函数(Hypothesis function)为：

其中

x=⎡⎣⎢⎢⎢⎢⎢⎢⎢x0x1x2⋮xn⎤⎦⎥⎥⎥⎥⎥⎥⎥,x0=1 x = [ x 0 x 1 x 2 ⋮ x n ] , x 0 = 1

θ=⎡⎣⎢⎢⎢⎢⎢⎢⎢θ0θ1θ2⋮θn⎤⎦⎥⎥⎥⎥⎥⎥⎥ θ = [ θ 0 θ 1 θ 2 ⋮ θ n ]

因为 θ θ 的取值有无数种，所以 h(x) h ( x ) 有无穷多个，这无穷多个 h(x) h ( x ) 组成了模型空间，而我们要做的就是从模型空间中找到对于我们的训练集来说最好的那个函数 h(x) h ( x ) ，那么对于我们的训练集来说这个函数的好坏是怎么定义的呢？这就到了我们的第二步，策略。

策略

一个最直观的方法是比较我们的 h(x) h ( x ) 对训练集中 x x 做出的预测与实际值之间的差距，我们将训练集中所有的 x x 都进行预测，然后将每一个与实际值之间的差距求平方加起来，这样就得到了线性模型的代价函数(cost function)：

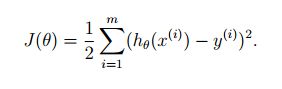
其中， 12 1 2 是为了后面求偏导方便而添加的。

这个代价函数也叫作最小乘代价函数(least-squares cost function).

现在我们已经找到了对函数的评价准则，那么我们下一步要做的就是按照这个评价准则从模型空间中找到最好的那个函数，显然，这个最好的函数能够使我们的评价准则最好，也就是能够使 J(θ) J ( θ ) 最小。那么我们下一步要做的就变成了最优化 J(θ) J ( θ ) ,找到能够使 J(θ) J ( θ ) 最小的参数变量 θ θ .

算法

我们现在的目标是找到能够使 J(θ) J ( θ ) 最小的参数变量 θ θ ,为此我们可以随机初始化 θ θ ,然后不断改变 θ θ 的值，直到 J(θ) J ( θ ) 小到在我们预期的范围内，如此我们便学习到了参数变量 θ θ , 也就从模型空间中挑出来了一个具体的函数，这个函数就是我们从训练集中学到的模型，接下来就可以用这个模型对未知的数据做出预测和分析了。

梯度下降法

梯度下降法就是具体的一种如何改变 θ θ 的方法。

梯度下降法是指按照梯度的方向改变 θ θ 的值，因为梯度的方向就是使得 J(θ) J ( θ ) 变化最快的方向。

α α 为学习率(learning rate)，决定了 θ θ 改变的大小，即决定了学习速度的快慢。

批量梯度下降

先求得

∂∂θjJ(θ)=∑i=1m(hθ(x(i))−y(i))x(i)j ∂ ∂ θ j J ( θ ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

然后更新 θ​ θ ​

θj=θj−α∑i=1m(hθ(x(i))−y(i))x(i)j θ j = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

可以看到每次更新 θ​ θ ​ 要用到训练集中的所有样本数据，也就是说每一次梯度下降(将 θ0到θn​ θ 0 到 θ n ​ 全部更新完)，要用到 x(1)到x(m)​ x ( 1 ) 到 x ( m ) ​ 所有样本，即

θ0=θ0−α∑i=1m(hθ(x(i))−y(i))x(i)j θ 0 = θ 0 − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

θ1=θ1−α∑i=1m(hθ(x(i))−y(i))x(i)j θ 1 = θ 1 − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

θn=θn−α∑i=1m(hθ(x(i))−y(i))x(i)j θ n = θ n − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

这种梯度下降方法就叫做批量梯度下降，每次更新 θ θ 要保证所有样本的代价函数之和变化最快。

如下所示：

随机梯度下降

批量梯度下降每次更新 θ θ 需要用到所有的样本，对于训练集中样本数比较大的时候是不方便的，因此有了随机梯度下降法。

随机梯度下降法是指每次更新 θ θ 的时候只考虑随机一个样本的梯度值，不去考虑所有样本的梯度值，每次更新 θ θ 只保证某一个样本的代价函数变化最快，即此时的代价函数变成了

J(θ)=12(hθ(x(i))−y(i))2 J ( θ ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2

求得

∂∂θjJ(θ)=(hθ(x(i))−y(i))x(i)j ∂ ∂ θ j J ( θ ) = ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

然后更新 θ θ

θj=θj−α(hθ(x(i))−y(i))x(i)j θ j = θ j − α ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

如下所示

小批量梯度下降

小批量梯度下降综合了上述两种方法，他在每次更新 θ θ 的时候选择K个样本，每次更新 θ θ 要保证这k个样本的代价函数之和变化最快。

如下所示

比较

在线性回归模型中，批量梯度下降总是能够找到全局最优，他每一步都是考虑全部样本代价函数的梯度，因而他的迭代次数要少，但样本数比较多的时候速度慢；

随机梯度下降不一定能够找到最优解，可能会在最优解附近徘徊，由于他每一步考虑的只是某个样本代价函数的梯度，所以他在迭代的过程中可能会发生全部样本的代价函数之和增加的现象，迭代次数比较多，但因为每次只考虑一个样本，速度较快；

小批量梯度下降则综合考虑了上述两者，但对于“小”的程度，则需要具体设计。