前言
Paxos算法是用来解决分布式系统中,如何就某个值达成一致的算法。它晦涩难懂的程度完全可以跟它的重要程度相匹敌。目前关于paxos算法的介绍已经非常多,但大多数是和稀泥式的人云亦云,却很少有人能对提出自己的见解。本文试图从不一样的角度来对Paxos made simple的论文进行解释,而不仅仅是对论文的拙劣翻译,希望即使没有看过论文的同学也能看懂。
一致性问题
为了实现集群的高可用性,用户的数据往往要多重备份,多个副本虽然避免了单点故障,但同时也引入了新的挑战。
假设有一组服务器保存了用户的余额,初始是100块,现在用户提交了两个订单,一个订单是消费10元,一个订单是充值50元。由于网络错误和延迟等原因,导致一部分服务器只收到了第一个订单(余额更新为90元),一部分服务器只收到了第二个订单(余额更新为150元),还有一部分服务器两个订单都接收到了(余额更新为140元),这三者无法就最终余额达成一致。这就是一致性问题。
一致性算法并不保证所有提出的值都是正确的(这可能是安全管理员的职责)。我们假设所有提交的值都是正确的,算法需要对到底该选哪个做出决策,并使决策的结果被所有参与者获悉。
一致性算法并不保证所有节点中的数据是完全一致的,但它能保证即使一小部分节点出现故障,仍然能对外提供一致的服务(客户端无感知)
在正式开始介绍Paxos所面临的难题前,为了表述方便,先提一下Paxos算法中的三个角色,后面会比较频繁的用到:
- Proposer:议案发起者。
- Acceptor:决策者,可以批准议案。
- Learner:最终决策的学习者。
我们虚拟一个一致性问题的场景:有一个用户小绿,现在要对他的姓氏信息进行修改,此时有多个不同的议案被提出,如何就最终的结果达成一致。
首先看一下下面这种最简单的情况:A1接受了Pa的议案“赵”,A2和A3接受了Pb的议案“钱”,那么最终小绿应该姓什么?
答案很简单:超过半数的的议案就是最终的选定值。小绿应该姓“钱”!在议案提交后,Pa和Pb只要查询一下小绿姓氏,很容易就能查到 “钱”的数量超过半数,因此Pb的议案将会返回“成功”,Pa的议案将会返回“失败”。
P0. 当集群中,超过半数的Acceptor接受了一个议案,那我们就可以说这个议案被选定了(Chosen)。
P0已经是一个完备的一致性算法,保证了P0也就解决了一致性问题。但是P0的实用性不佳,一个议案想被半数以上的Acceptor接受是一件极其困难的事情!
看下面这种情况:A1,A2,A3分别接受了“赵”,“钱”,“孙”,结果没有任何一个议案形成多数派,所有的议案都将返回“失败”。议案的数量越多,那议案被选定的概率就越低,这显然是没法容忍的。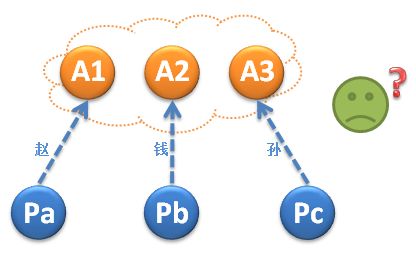
要解决这个问题,必须允许一个Acceptor接受多个议案,后接受的议案可以覆盖掉之前接受的议案。
如下图所示, A1已经接受了“赵”,A2已经接受了“钱”,此时Pc提出了“孙”,并被A1,A2,A3接受,这样就解决了无法形成多数派的问题。
但现在又会面临下图中的新问题:A1,A2,A3已经接受了“赵”,此时我们认为“赵”是被选定的,但此时偏偏Pb和Pc不识时务,Pb向A2提出了“钱”,Pc向A3提出了“孙”。这样就从一致性状态,又回到了不一致的状态…这显然破坏了一致性。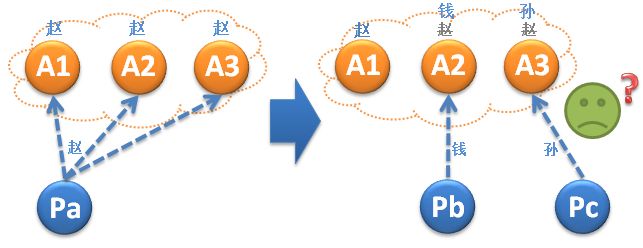
Paxos就是在上述背景下产生的,Paxos要实现的目标的是:
T1.一次选举必须要选定一个议案(不能出现所有议案都被拒绝的情况)
T2.一次选举必须只选定一个议案(不能出现两个议案有不同的值,却都被选定的情况)
Paxos算法的推导
首先,Paxos算法的必须要能满足第一个条件:
P1:一个Acceptor必须接受它收到的第一个议案。
要满足这个条件实在太过简单了,方法略。。。
下面是我个人对这个条件的理解,为什么必须满足这个条件:
假设只有一个Acceptor,只有一个Proposer。如果Acceptor出于某些原因拒绝了Proposer的议案,那必然导致Paxos的目标T1无法达成。因此可以认为目标T1隐含了P1。
在开始P2的推导的前,为了区分不同议案,需要先对每个Proposer的议案进行编号,编号时必须保证每个议案的编号具有唯一性(不讨论实现方法),而且编号是不断增大的。
Paxos的目标T2隐含了P2:
P2:如果一个值为v的议案被选定了,那么被选定的更大编号的议案,它的值必须也是v。
P2很容易理解,除了其中的一个形容词更大编号的,这个形容词很扎眼,为什么只对更大编号的议案进行限制,更小的编号怎么办? 老头子给的解释很简单“By induction on proposal number”(如果不看论文后半部分,没人知道他在说什么…)我说一下我自己的理解:
首先把“更大编号的”几个字换成“其他的”,我们称它为P2S。那么P2S能否满足Paxos的目标?答案是肯定的。然后比较P2和P2S,谁的约束更强?这得看“更小的编号”是怎么处理的,从论文后面的推演来看更小编号的议案绝对不允许被选定!!!因此满足P2的议案是P2S的一个子集。
显而易见,P2S和P2都能满足Paxos目标。换句话说,能满足Paxos目标的办法很多,但我们只选其中一个办法就OK了。不过,要选最简单的办法(看完后面就知道了)。
总之,现在我们可以得出一个结论:
如果P1和P2都能够被满足,那么Paxos的两个目标就能够达成。 如果你对上面这个结论没有异议,那么就说明你已经充分理解了P1和P2。
接下来就需要想办法,如何才能满足P2:议案在选定前,都要先被Acceptor接受,因此要满足P2,我们只要满足下面的条件:
P2a:如果一个值为v的议案被选定了,那么Acceptor接受的更大编号的议案,它的值必须也是v。
P2a是P2的充分条件,但是P2a存在一个大麻烦:当一个议案被选定后,一部分Acceptor无法立刻获得通知。例如下图中A1和A2已经接受了“赵”,这时“赵”就被选定了,此时Pb向A3提出了一个议案“钱”,这是A3接受的第一个议案,为了满足P1,A3必须接受这个议案,此时就会导致P2a无法被满足了。
为了解决上述的问题,我们想一下:要是此时不让Pb提出“钱”这个议案,而是提出“赵”这议案就万事大吉了。顺着这个思路,我们得到了P2b:
P2b:如果一个值为v的议案被选定了,那么Proposer提出的更大编号的议案,它的值必须也是v。
P2b是一个比P2a更强的约束,也就是说P2b是P2a的充分条件,只要能满足P2b,那P2a就自动满足。但P2b很难被满足,考虑下图这种情况,A1接受了议案“赵”,A2即将接受议案“赵”,此时Pb提出了一个议案“钱”,这种情况下我们又会遇到跟P2a完全相同的麻烦。
很明显,要想满足P2b,我们必需让Proposer拥有“预测未来”的能力,这听起来像在讲鬼故事,后面会想办法解决这一点。 在介绍如何“预测未来”之前,我们必须先确定Proposer在提出一个议案时,它的值该如何选取,因为取值的方法决定了“预测”的方法。
一个理所当然的取值方法:找到一个Acceptor的多数派的集合,集合内被接受的议案的值都是v,此时Proposer提出一个新的议案,议案的值必须也是v;如果没有这样的多数派集合,那Proposer就任意提。
这个取值方法,完全能符合P2b,这是一目了然的,但问题出在 “预测”上,我们必须能预测到即将形成多数派的那个议案,如果有谁能做到那就真的是在讲鬼故事了。
Proposal提出议案的正确姿势:
P2c:在所有Acceptor中,任意选取半数以上的Acceptor集合,我们称这个集合为S。Proposal新提出的议案(简称Pnew)必须符合下面两个条件之一:
1)如果S中所有Acceptor都没有接受过议案的话,那么Pnew的编号保证唯一性和递增即可,Pnew的值可以是任意值。
2)如果S中有一个或多个Acceptor曾经接受过议案的话,要先找出其中编号最大的那个议案,假设它的编号为N,值为V。那么Pnew的编号必须大于N,Pnew的值必须等于V。
P2c提出议案的规则有点复杂,它真的能满足P2b吗?至少看上去不是那么一目了然…..老头子用了归纳法来证明P2c能满足P2b,但效果不佳,没什么人能看懂,所以下面的证明过程即使你看不懂也必要太沮丧(后面会给出图文解释)。
证明题(注意!前方高能):
已知议案 $(m, v_a)$,是集合中第一个被选定的议案,接受这个议案的Acceptor集合为 $S_m$,在满足P2c的规则2的情况下,提出了一个新的议案 $(n, v_b)$,其中$n>m$,证明$v_b = v_a$
-
证明初始成立:当议案的编号$n = m+1$时,证明$v_b = v_a$
因为$(m, v_a)$是第一个被选定的议案,因此在$m+1$提出之前,$m$必然是集群当中编号最大的议案。
根据P2c的规则2,议案$(m+1,v_b)$能够被提出,是因为存在一个多数派集合$S_n$,这个集合中,编号最大的议案的值为$v_b$。因为$Sm$和$Sn$都是多数派集合,所以他们必定存在交集。交集中的Acceptor必定都接受了$(m,v_a)$,$m$是整个集群最大的编号,当然也是$S_n$中最大的编号,根据P2c的规则2,议案$m+1$的值只能是$v_a$,若$v_b$不等于$v_a$,将导致矛盾,因此$v_b = v_a$ -
当$n > m+1$时,假设编号从$m+1$到$n-1$的议案的值都是$v_a$,证明$v_b = v_a$
编号为$m+1$到$n-1$的议案提出后,我们没办法判断究竟那一个议案会被选定,但有一点是可以肯定的:所有接受了$v_a$的Acceptor构成了一个新的集合$S_{n-1}$,这个集合包含了集合$Sm$中的所有Acceptor,$S_{n-1}$显然是一个多数派集合,这个集合接受的议案的编号在$m$到$n-1$之间,而且值为$v_a$。没有包含在集合$S_{n-1}$中的Acceptor所接受的议案一定小于$m$。
根据P2c的规则2,议案$(n,v_b)$能够被提出,那么一定存在一个多数派集合$Sn$,$Sn$中接受的最大编号的议案的值为$v_b$。因为$S_n$和都$S_{n-1}$是多数派集合,所以他们必定存在交集。交集中的议案的最大编号一定在$m$到$n-1$之间。因此$S_n$集合中编号最大的议案一定位于交集内。根据P2c的规则,此时$v_b$必定等于$v_a$。
这个证明过程,如果你能看懂,请受我三跪。。。
接下来,上图,举例说明。
假设有一个议案(3,Va)提交后,这个议案成为了被Acceptor集群选定的第一个议案 ,那此时集群的状态可能会如下图所示:
一共5个Acceptor,有3个Acceptor接受了议案(3,Va),刚刚过半。此时有一个编号为4的议案要提出,根据P2c的规则2,首先选一个过半的集合,就选上图中蓝色线圈出来的A3,A4,A5好了(任意选),这个集合中编号最大的议案是(3,Va),因此新提出的议案必定为(4,Va)。符合P2b。
议案(4,Va)提出后,集群的状态可能是下面这样:
此时再提出编号为5或6,7,8,9,10的议案,这个议案的值必定也是Va(不信的话请举出反例),符合P2b。依此类推。。。
由此可证,P2c是能够满足P2b的!!!
想想看P2,P2a,P2b中为什么一定要有“更大编号的”这几个扎眼的字眼,此时你应该能有一点感觉了,可能你会把它理解成“后提出的”,如果你是这样理解的话,请往下看。
有些童鞋肯定早就已经想到了:当议案(3,Va)提交后,这个议案成为了被Acceptor集群选定的第一个议案,此时集群的状态有没有可能是下面这样?
注意,这时议案(4,Vb)才是集群当中的编号最大的议案,要是这样就糟糕了!当我们提出编号为5的议案时,它的取值就有可能是Vb,导致无法满足P2b。
为了保证不出现这种情况,就要用到前面提到的“预测未来”的能力。跟P2c的议案规则相配套的,需要预测的未来是:
当一个议案在提出时(即使已经在发送的半路上了),它必须能够知道当前已经提出的议案的最大编号。
这样的话,议案(3,Va)提交时,就会知道有一个(4,Vb)的议案已经提交了,然后将自己的编号改成5或更大编号提交,一切就完美了。
但是你知道的,我们并不可能真的预测未来,换个思路,议案肯定是要提交给Acceptor的,只要由Acceptor来保证议案编号的顺序就OK了。于是有:
议案(n,v)在提出前,必须将自己的编号通知给半数以上的Acceptor。收到通知的Acceptor将n跟自己之前收到的通知进行比较,如果n更大,就将n确认为最大编号。当半数以上Acceptor确认n是最大编号时,议案(n,v)才能正式提交。
两个编号不同的议案,不可能同时被确认为最大编号,证明略。
但是实际环境上,上面的条件还不足以保证议案被接受的顺序,比如议案(n,Va)被确认为最大编号后,开始向Acceptor发送,此时(n+1,Vb)提出,由于网络速度的原因,(n+1,Vb)可能比(n,Va)更早被Acceptor接收到。
因此Acceptor收到一个新的编号n,在确认n比自己之前收到的编号大时,必须做出承诺(Promise):不再接受比n小的议案。
这个承诺会导致部分漏网之鱼(在发送途中被抢走最大编号的议案),无法形成多数派。
例如下图所示:有一个在途的议案(1,Va),当A2和A3对议案(2,Vb)做出承诺的同时,(1,Va)就失去了形成多数派的权利。
至此,我们就形成了一个完整的算法(具体实现请自行搜索PhxPaxos)。
后记
算法原文中,将Promise看做是P2c的具体实现,而我们将Promise看成是弥补P2c的补充条件。这两者没有质的差别,只是角度不同,我个人认为后一种更容易被理解,所以采用了后一种。不过采用后一种会遇到下面的麻烦:
按下面的顺序提交议案:
①议案(1,Va)向A1发送Prepare,获得A1的承诺。
②议案(2,Vb)向A1发送Prepare,获得A1的承诺。
③发送议案(1,Va)
此时A1会拒绝议案(1,Va)
采用后一种解释的话,会发现A1拒绝议案(1,Va)是违反了P1的,而采用前一种解释则不违反P1。(这不过是个文字游戏,我已经懒的去思考了,就这样吧)
如果我们将半数以上的Acceptor对同一个议案(n,v)做出承诺的状态称作是“锁定”状态。那么这个“锁定”状态具有以下性质:
排它性: 所有比n小的议案都不允许提交,已经在途的议案,则不允许其形成多数派。
唯一性: 任意时刻,全局只有一个议案能获得“锁定”状态。
原子性: 议案n从锁定状态变为非锁定状态的过程是原子的,议案n+1从非锁定状态变更为锁定状态的过程也是原子的。
我相信,正是上面的这三条性质保证了一致性。
最后,感谢老头子给出的如此精彩的算法。