SMPL模型进阶
SMPL模型是一种参数化人体模型,是马普所提出的一种人体建模方法,该方法可以进行任意的人体建模和动画驱动。这种方法与传统的LBS的最大的不同在于其提出的人体姿态影像体表形貌的方法,这种方法可以模拟人的肌肉在肢体运动过程中的凸起和凹陷。因此可以避免人体在运动过程中的表面失真,可以精准的刻画人的肌肉拉伸以及收缩运动的形貌。
该方法中β和θ是其中的输入参数,其中β代表是个人体高矮胖瘦、头身比等比例的10个参数,θ是代表人体整体运动位姿和24个关节相对角度的75个参数。
β参数是ShapeBlendPose参数,可以通过10个增量模板控制人体形状变化: 具体而言:每个参数控制人体形态的变化可以通过动图来刻画:
PoseBlendShape参数是给出肌肉的凸起与凹下去与人体姿态,但是一般都优化算法都不采用poseBlendShape参数,因为PoseBlendShape项的惩罚能量的Landscape不利于非线性优化算法的迭代优化。
但是如果要与Kinect给出的25个参数进行匹配直接进行是不够的,因为两者的关节节点是不匹配的。其中原因在于SMPL不但需要考虑基本的人体构型,还需要考虑关节密度能否控制点的运动,因此胸部并无明显关节的情况下,增加了几个关节,而手上的关节数量较少。此外需要注意因为SMPL为了较好的人体模型表达,因此较为精细的部位增加了较多的点数,如手指部分,按照正常人面积应该点数较少,但这对于SMPL模型不利。
按照doublefusion的思路可以用测地线距离(geodesic distance)为度量进行简化,简化后的模型为了保证关节的正确性,需要额外加入关节附近的顶点索引,此外由于顶点的抽离,在weights、Jregressor、Shape_Tensor、Mean-vertices都应该相应变化,并重新利用Python等语言的脚本进行处理写成新的模型文件(.pkl或Json)。
在实际的关节运动中,由于是级联的铰链的运动(Articulated),因此在CPU或者GPU中都需要进行顺序运算,类似于Ai=Ai-1*Bi,从根节点出发到肢体关节点遍历类似于比遍历一棵特定深度的树,而树的深度决定顺序运算的最长链,树深度越长并行性越差,按照SMPL原始定义从尾骨位置出发的三叉树深度为9,在此种情况下GPU的单个warp最后的两个if会出问题,树的叶子节点深度分别为6,9,9, 5,5,而修改根节点为原来3号节点后,叶子节点的深度变为4,7,7,7,7,因此树深度下降,树平衡性增加,求解节点旋转平移的并行性提高。有望提高节点RT计算速度以及提高后续雅各比矩阵的稀疏性。
Json的索引需要重新排布,
对照表:
smpl [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
new: [ 3 7 8 1 12 13 0 16 17 2 20 21 4 5 6 9 10 11 14 15 18 19 22 23 ]
之前写错成了:(21号重复了两遍)
new: [ 3 7 8 1 12 13 0 16 17 2 20 21 4 5 6 9 10 11 14 21 18 19 22 23 ]
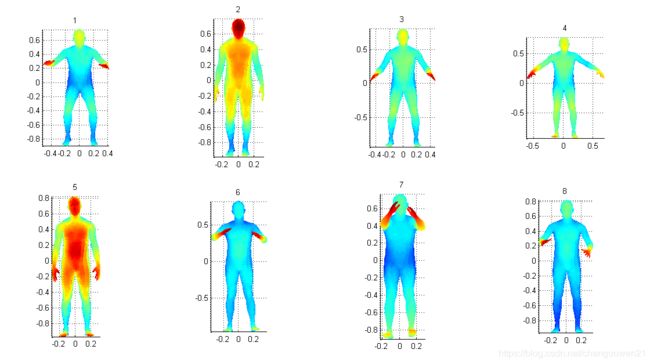
GMM的默认的8个中心姿态:
更改后的关节点编号 原始的关节点编号
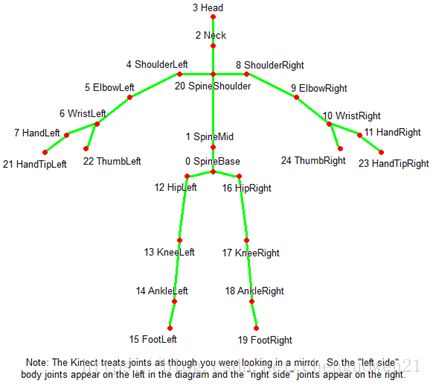
Kinect关节点 SMPL模型关节点
我整理的kinect与SMPL模型关节点对应关系如上图和下表所示, 但并非严格的对应关系。
Table = [ 0 16 12 1 17 13 18 14 15 19 20 4 8 9 10 5 6 7 11 ; %% Kinect
0 1 2 3 4 5 7 8 11 10 12 17 16 18 20 19 21 23 24 ]; %% SMPL
此外从Kinect中人体姿态为T-pose时候可以直接推出人体的部分β参数,如关于人体高矮、头身比例、肢体相关的比例等,但是不能得到胖瘦相关的参数,根据实际实验可以得到前五个参数,后面五个参数较难获得,甚至会因为无法获得而取得较大数值,导致人体模型严重失真。
为了对人体模型进行约束,作者还给了人体姿态的GMM模型参数,该模型由八个中心构成。 其中最大概率的GMM的并非为人站成T-pose状态下。 在利用GMM作为非线性优化重建人体模型相关研究中,GMM一般以对数的形式出现,但是此时需要注意的是目标惩罚函数并非以原始的概率密度的对数作为优化项,而是有一个constant项,甚至为了符合一般性,会先计算出贡献最大的多分布中在特定姿态下概率密度最大的分布,然后乘以相应的固定常数,然后进行优化。