面向过程编程
核心是过程二字,过程即解决问题的步骤,基于面向过程去设计程序就像是在设计一条工业流水线,是一种机械式的思维方式
优点:程序结构清晰可以把复杂的问题简单化,流程化
缺点:可扩展性差,一条流线只是用来解决一个问题
应用场景:linux内核,git,httpd,shell脚本
练习:过滤目录下文件内容包含error的文件
grep –rl ‘error’ /dir
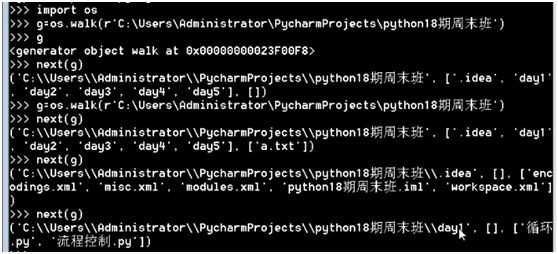
使用os模块walk方法:
os.walk会把目录下的二级目录和文件做成一个迭代器,多次使用实现文件路径的拼接
#grep -rl 'error' /dir/
import os
def init(func):
def wrapper(*args,**kwargs):
g=func(*args,**kwargs)
next(g)
return g
return wrapper
#第一阶段:找到所有文件的绝对路径
@init
def search(target):
while True:
filepath=yield
g=os.walk(filepath)
for pardir,_,files in g:
for file in files:
abspath=r'%s\%s' %(pardir,file)
target.send(abspath)
#第二阶段:打开文件
@init
def opener(target):
while True:
abspath=yield
with open(abspath,'rb') as f:
target.send((abspath,f))
#第三阶段:循环读出每一行内容
@init
def cat(target):
while True:
abspath,f=yield #(abspath,f)
for line in f:
res=target.send((abspath,line))
if res:break
#第四阶段:过滤
@init
def grep(pattern,target):
tag=False
while True:
abspath,line=yield tag
tag=False
if pattern in line:
target.send(abspath)
tag=True
#第五阶段:打印该行属于的文件名
@init
def printer():
while True:
abspath=yield
print(abspath)
g = search(opener(cat(grep('error'.encode('utf-8'), printer()))))
g.send(r'D:\python location\python36\day05\a')
3、递归
递归调用:在调用一个函数的过程中,直接或间接地调用了函数本身
Python中的递归在进行下一次递归时必须要保存状态,效率低,没有优化手段,所以对递归层级做了限制(其他编程语言中有尾递归方式进行优化)
1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3. 递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
尾递归优化:http://egon09.blog.51cto.com/9161406/1842475
#直接
def func():
print('from func')
func()
func()
输出:
from func
from func
…
from funcTraceback (most recent call last):
File "D:/python location/python36/day05/递归.py", line 8, in
func()
[Previous line repeated 993 more times]
RecursionError: maximum recursion depth exceeded while calling a Python object #调用Python对象时的最大递归深度超过了限制
如果递归层级过多,会报如上错误
#间接
def foo():
print('from foo')
bar()
def bar():
print('from bar')
foo()
foo()
输出:
RecursionError: maximum recursion depth exceeded while calling a Python object #调用Python对象时的最大递归深度超过了限制
修改递归层级限制(默认1000)
>>> import sys >>> sys.getrecursionlimit() 1000 >>> sys.setrecursionlimit(2000) >>> sys.getrecursionlimit() 2000
练习:
已知:
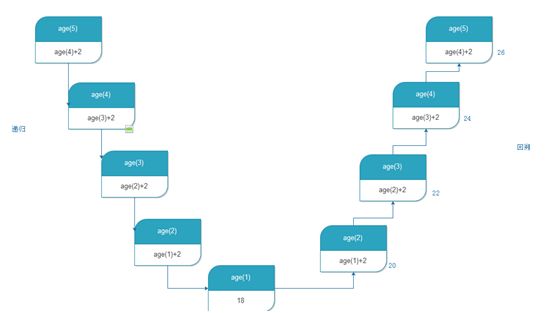
age(5)=age(4)+2
age(4)=age(3)+2
age(3)=age(2)+2
age(2)=age(1)+2
age(1)=18
首先做判断:
age(n)=age(n-1)+2 #n>1
age(1)=18 #n=1
def age(n): if n == 1: return 18 return age(n-1)+2 print(age(5))
递归的执行分为两个阶段:
1 递推
2 回溯
递归和循环功能差不多,但在不知道循环次数时适合使用递归
练习:
取出列表中所有的元素
l =[1, 2, [3, [4, 5, 6, [7, 8, [9, 10, [11, 12, 13, [14,15,[16,[17,]],19]]]]]]] # def search(l): for item in l: if type(item) is list: search(item) else: print(item) search(l)
4、二分法
方法:
判断一个数值是否存在于一个特别大的列表中,如果使用in方法会遍历列表,占内存过多,使用二分法每次会平分列表,占用内存较少
练习:
#二分法
l = [1,2,5,7,10,31,44,47,56,99,102,130,240]
def binary_search(l,num):
print(l) #[10, 31]
if len(l) > 1:
mid_index=len(l)//2 #1
if num > l[mid_index]:
#in the right
l=l[mid_index:] #l=[31]
binary_search(l,num)
elif num < l[mid_index]:
#in the left
l=l[:mid_index]
binary_search(l,num)
else:
print('find it')
else:
if l[0] == num:
print('find it')
else:
print('not exist')
return
binary_search(l,32)