大数据分析案例：财政收入预测分析

财政收入，是指政府为履行其职能、实施公共政策和提供公共物品与服务需要而筹集的一切资金的总和。
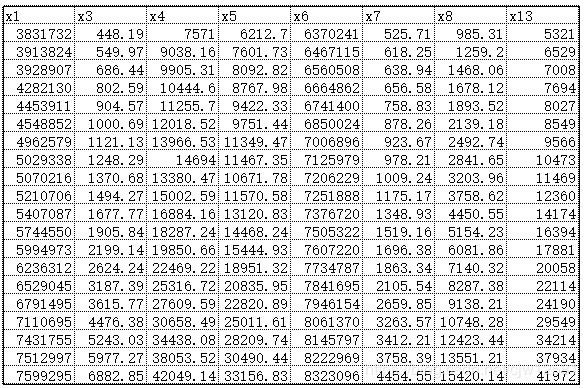
财政收入预测数据基础情况：
对1994年至2013年的数据进行分析，本次数据分析建模目标主要有2个：
1.分析、识别影响地方财政收入的关键特征
2.预测2014年和2015年的财政收入

---

方法选择——最小二乘估计方法
建立财政收入与各待定的影响因素之间的多元线性回归模型，运用最小二乘估计方法来估计回归模型的系数，通过系数来检验它们之间的关系，模型的结果对数据的依赖程度很大，并且普通最小二乘估计求得的解往往是局部最优解，后续步骤的检验可能就会失去应有的意义。
方法选择——Lasso特征选择方法
运用Lasso特征选择方法来研究影响地方财政收入的因素。在Lasso特征选择的基础上，鉴于灰色预测对少量数据预测的优良性能，对单个选定的影响因素建立灰色预测模型，得到它们在2014年及2015年的预测值。由于支持向量回归较强的适用性和容错能力，对历史数据建立训练模型，把灰色预测的数据结果代入训练完成的模型中，充分考虑历史数据信息，可以得到较为准确的预测结果，即2014年和2015年财政收入。

---

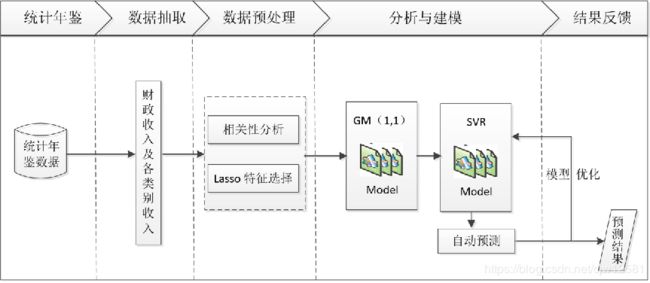
总体流程主要包括以下步骤：
1 对原始数据进行探索性分析

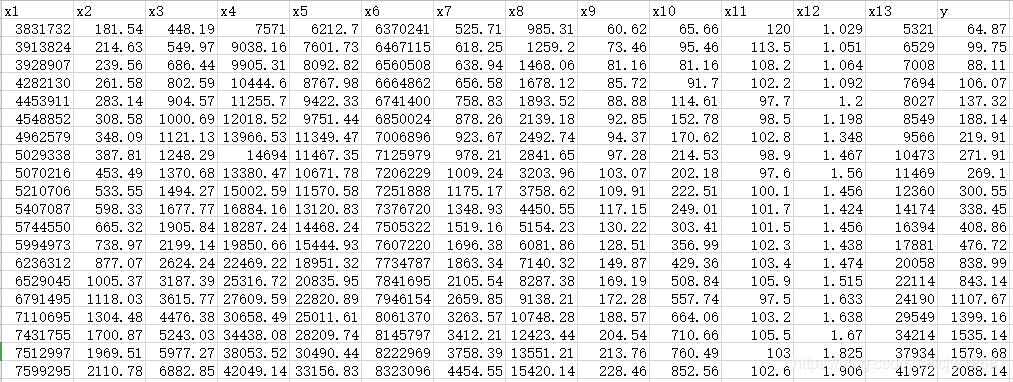
2. 了解原始特征之间的相关性。 利用Lasso特征选择模型进行特征提取
3. 建立单个特征的灰色预测模型以及支持向量回归预测模型。
4. 使用支持向量回归预测模型得出2014-2015年财政收入的预测值
5. 财政收入预测模型进行评价

---

Pearson相关系数
相关性分析是指对两个或多个具备相关性的特征元素进行分析,从而衡量两个特征因素的相关密切程度。
在统计学中,常用Pearson相关系数来进行相关性分析。
Pearson相关系数是用来度量两个特征X和Y之间的相互关系(线性相关的强弱) , 是最简单的一种相关
系数,通常用r或p表示,取值范围在[-1,1]之间。.
Pearson相关系数的一个关键的特性就是它不会随着特征的位置或是大小的变化而变化。

Lasso回归方法
Lasso回归方法属于正则化方法的一种，是压缩估计。
它通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些系数，同时设定一些系数为零，保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。
原理：Lasso以缩小特征集（降阶）为思想，是一种收缩估计方法。
Lasso方法可以将特征的系数进行压缩并使某些回归系数变为0，进而达到特征选择的目的，可以广泛地应用于模型改进与选择。
通过选择惩罚函数，借用Lasso思想和方法实现特征选择的目的。这种过程可以通过优化一个“损失”“惩罚”的函数问题来完成。

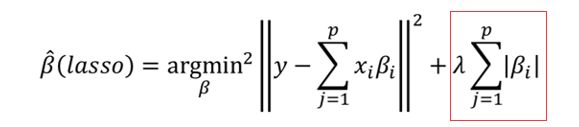
其中,$\lambda$为非负正则参数,控制着模型的复杂程度,$\lambda$越大对特征较多的线性模型的惩罚力度就越大,从而最终获得一 个特征较少的模型, 红框称为惩罚项。调整参数的确定可以采用交叉验证法,选取交叉验证误差最小的A值。最后,按照得到的值,用全部数据重新拟合模型即可。

适用于：当原始特征中存在多重共线性时，Lasso回归不失为一种很好的处理共线性的方法，它可以有效地对存在多重共线性的特征进行筛选。
在机器学习中，面对海量的数据，首先想到的就是降维，争取用尽可能少的数据解决问题，从这层意义上说，用Lasso模型进行特征选择也是一种有效的降维方法。
Lasso从理论上说，对数据类型没有太多限制，可以接受任何类型的数据，而且一般不需要对特征进行标准化处理。

优点：可以弥补最小二乘法和逐步回归局部最优估计的不足，可以很好地进行特征的选择，可以有效地解决各特征之间存在多重共线性的问题。
缺点：如果存在一组高度相关的特征时，Lasso回归方法倾向于选择其中的一个特征，而忽视其他所有的特征，这种情况会导致结果的不稳定性。
虽然Lasso回归方法存在弊端，但是在合适的场景中还是可以发挥不错的效果。在财政收入预测中，各原始特征存在着严重的多重共线性，多重共线性问题已成为主要问题，这里采用Lasso回归方法进行特征选取是恰当的。

import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso

inputFile = 'data.csv'            # 输入的数据文件
outputFile = 'new_reg_data.csv'   # 输出的数据文件
data = pd.read_csv(inputFile)     # 读取数据
pearson = np.round(data.corr(method='pearson'), 2)   # 保留两位小数
print('相关系数矩阵为：', pearson)

lasso = Lasso(1000)               # 调用Lasso()函数，设置λ的值为1000
lasso.fit(data.iloc[:, 0:13], data['y'])
print('相关系数为：', np.round(lasso.coef_, 5))           # 输出结果，保留五位小数
print('相关系数非零个数为：', np.sum(lasso.coef_ != 0))   # 计算相关系数非零的个数

mask = lasso.coef_ != 0                 # 返回一个相关系数是否为零的布尔数组
new_reg_data = data.iloc[:, mask]       # 返回相关系数非零的数据
new_reg_data.to_csv(outputFile, index=None)         # 存储数据
print('输出数据的维度为：', new_reg_data.shape)      # 查看输出数据的维度
# 相关系数为： [-1.8000e-04 -0.0000e+00  1.2414e-01 -1.0310e-02  6.5400e-02  1.2000e-04
#   3.1741e-01  3.4900e-02 -0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
#  -4.0300e-02]

结果（剔除权值为0的列）：

---

灰色预测算法
灰色预测法是一种对含有不确定因素的系统进行预测的方法。
在建立灰色预测模型之前，需先对原始时间序列进行数据处理，经过数据处理后的时间序列即称为生成列。
灰色系统常用的数据处理方式有累加和累减两种。

import numpy as np


def gm11(x0):
    '''
    #自定义灰色预测函数
    :param x0:
    :return:
    '''
    x1 = x0.cumsum()                    # 1-AGO序列
    z1 = (x1[:len(x1)-1] + x1[1:])/2.0  # 紧邻均值（MEAN）生成序列
    z1 = z1.reshape((len(z1), 1))
    B = np.append(-z1, np.ones_like(z1), axis=1)
    Yn = x0[1:].reshape((len(x0)-1, 1))
    [[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn)        # 计算参数
    f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2))    # 还原值
    delta = np.abs(x0 - np.array([f(i) for i in range(1, len(x0)+1)]))
    C = delta.std()/x0.std()
    P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
    return f, a, b, x0[0], C, P   # 返回灰色预测函数、a、b、首项、方差比、小残差概率

适用于：灰色预测法的通用性比较强些，一般的时间序列场合都可以用，尤其适合那些规律性差且不清楚数据产生机理的情况。

优点：具有预测精度高、模型可检验、参数估计方法简单、对小数据集有很好的预测效果。
缺点：对原始数据序列的光滑度要求很高，在原始数据列光滑性较差的情况下灰色预测模型的预测精度不高甚至通不过检验，结果只能放弃使用灰色模型进行预测。

import numpy as np
import pandas as pd
from gm11 import gm11

inputFile = 'new_reg_data.csv'   # 输入的数据文件
inputFile1 = 'data.csv'          # 输入的数据文件
new_reg_data = pd.read_csv(inputFile)   # 读取经过特征选择后的数据
data = pd.read_csv(inputFile1)          # 读取总的数据
new_reg_data.index = range(1994, 2014)
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
col = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']

for i in col:

    f = gm11(new_reg_data.loc[range(1994, 2014), i].as_matrix())[0]
    new_reg_data.loc[2014, i] = f(len(new_reg_data)-1)    # 2014年预测结果 len()：列长
    new_reg_data.loc[2015, i] = f(len(new_reg_data))      # 2015年预测结果
    new_reg_data[i] = new_reg_data[i].round(2)            # 保留两位小数
# new_reg_data.loc[2014, i] 当i=x13时：
# Out[23]: 44506.47
# len(new_reg_data)
# Out[24]: 22
outputFile = 'new_reg_data_GM11.xls'            # 灰色预测后保存的路径
y = list(data['y'].values)                      # 提取财政收入列，合并至新数据框中
y.extend([np.nan, np.nan])   # y列新增两行 NaN
new_reg_data['y'] = y
new_reg_data.to_excel(outputFile)                        # 结果输出
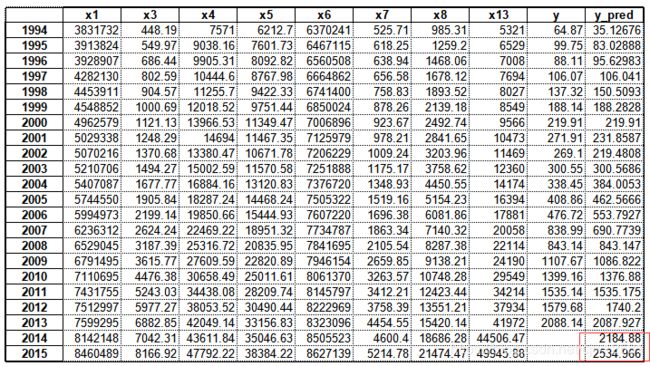
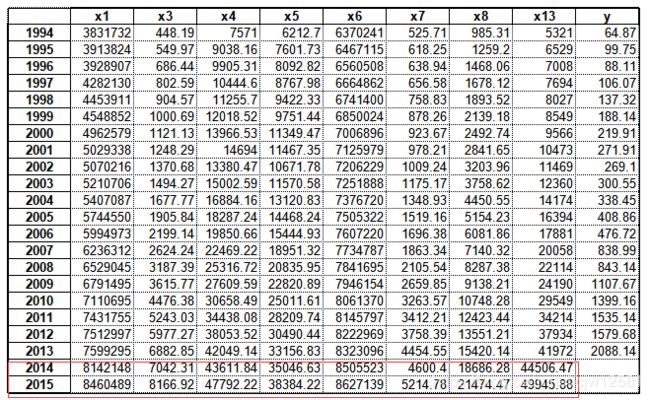
print('预测结果为：', new_reg_data.loc[2014: 2015, :])   # 预测结果展示

结果为：

SVR算法
sklearn库的LinearSVR函数实现了线性支持向量回归，其使用语法如下：
class sklearn.svm.LinearSVR(epsilon=0.0, tol=0.0001, C=1.0, loss=’epsilon_insensitive’…)
max_iter 接收int。指定最大迭代次数，默认为1000。
由于支持向量机拥有完善的理论基础和良好的特性，人们对其进行了广泛的研究和应用，涉及分类、回归、聚类、时间序列分析、异常点检测等诸多方面。

优点：支持向量回归不仅适用于线性模型，对于数据和特征之间的非线性关系也能很好抓住；支持向量回归不需要担心多重共线性问题，可以避免局部极小化问题，提高泛化性能，解决高维问题；支持向量回归虽然不会在过程中直接排除异常点，但会使得由异常点引起的偏差更小。
缺点：计算复杂度高，在面临数据量大的时候，计算耗时长。

使用sklearn构建的SVR模型属性及其说明如下表所示：

 def fit(self, X, y, sample_weight=None):
        """Fit the model according to the given training data.

        Parameters
        ----------
        X : {array-like, sparse matrix}, shape = [n_samples, n_features]
            Training vector, where n_samples in the number of samples and
            n_features is the number of features.

        y : array-like, shape = [n_samples]
            Target vector relative to X

import pandas as pd
from sklearn.svm import LinearSVR
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示，否则可能无法显示中文或者是各种字符错乱
plt.rcParams['axes.unicode_minus'] = False

inputFile = 'new_reg_data_GM11.xls'              # 灰色预测后保存的路径
data = pd.read_excel(inputFile, index_col=0)     # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
data_train = data.loc[range(1994, 2014)].copy()  # 取2014年前的数据建模 .copy()防止数据data被改变

data_mean = data_train.mean()  # 求平均值
data_std = data_train.std()  # 求标准差值
data_train = (data_train - data_mean)/data_std   # 数据标准化
'''标准化后数据 data_train'''
#             x1        x3        x4  ...        x8       x13         y
# 1994 -1.384721 -1.001807 -1.183344  ... -1.054057 -1.075938 -0.908018
# 1995 -1.319682 -0.948774 -1.039547  ... -0.992899 -0.967199 -0.850768
# 1996 -1.307732 -0.877665 -0.954558  ... -0.946262 -0.924082 -0.869873
# 1997 -1.027884 -0.817144 -0.901702  ... -0.899357 -0.862331 -0.840394
# 1998 -0.891787 -0.764006 -0.822206  ... -0.851259 -0.832356 -0.789102
# 1999 -0.816568 -0.713922 -0.747442  ... -0.796405 -0.785368 -0.705689
# 2000 -0.488784 -0.651165 -0.556517  ... -0.717457 -0.693822 -0.653543
# 2001 -0.435893 -0.584907 -0.485218  ... -0.639547 -0.612178 -0.568193
# 2002 -0.403507 -0.521135 -0.613957  ... -0.558646 -0.522522 -0.572805
# 2003 -0.292201 -0.456737 -0.454973  ... -0.434793 -0.442319 -0.521184
# 2004 -0.136614 -0.361123 -0.270560  ... -0.280290 -0.279030 -0.458977
# 2005  0.130748 -0.242285 -0.133043  ... -0.123162 -0.079196 -0.343410
# 2006  0.329151 -0.089458  0.020188  ...  0.083972  0.054657 -0.232028
# 2007  0.520357  0.132044  0.276833  ...  0.320320  0.250621  0.362584
# 2008  0.752281  0.425479  0.555917  ...  0.576452  0.435693  0.369396
# 2009  0.960212  0.648690  0.780642  ...  0.766437  0.622566  0.803582
# 2010  1.213105  1.097119  1.079465  ...  1.125956  1.104959  1.282019
# 2011  1.467472  1.496590  1.449903  ...  1.500009  1.524882  1.505210
# 2012  1.531837  1.879172  1.804253  ...  1.751833  1.859740  1.578316
# 2013  1.600209  2.351033  2.195865  ...  2.169154  2.223223  2.412877

x_train = data_train[feature].values             # 特征数据
y_train = data_train['y'].values                 # 标签数据
svr = LinearSVR(max_iter=10000)                  # 调用LinearSVR()函数
svr.fit(x_train, y_train)                        # 模型训练
#LinearSVR(C=1.0, dual=True, epsilon=0.0, fit_intercept=True,
#           intercept_scaling=1.0, loss='epsilon_insensitive', max_iter=10000,
#           random_state=None, tol=0.0001, verbose=0)

x = ((data[feature] - data_mean[feature])/data_std[feature]).values  # 预测，并还原结果。
data[u'y_pred'] = svr.predict(x) * data_std['y'] + data_mean['y']
# svr.predict(x)值如下：
# array([-0.95679683, -0.87818492, -0.85752099, -0.8404333 , -0.76744221,
#        -0.70544665, -0.65354974, -0.63395572, -0.6542656 , -0.52117245,
#        -0.38423108, -0.25528617, -0.10555373,  0.11927907,  0.36936224,
#         0.76935001,  1.24543625,  1.50521006,  1.841692  ,  2.41243839,
#         2.57161102,  3.14622657])

outputFile = 'new_reg_data_GM11_revenue.xls'     # SVR预测后保存的结果
data.to_excel(outputFile)
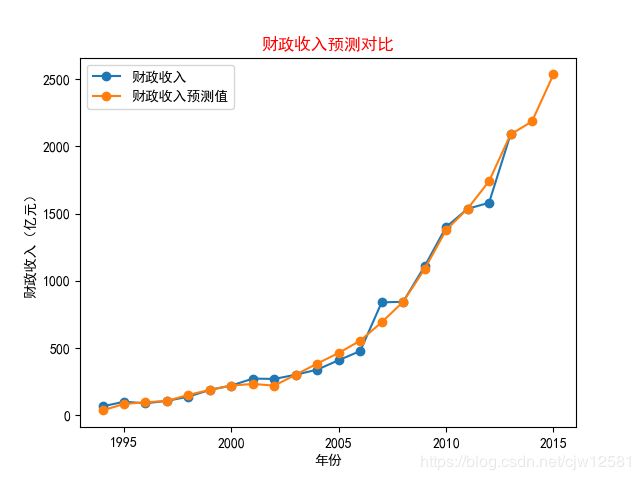
plt.title('财政收入预测对比', color='r')
plt.xlabel('年份')
plt.ylabel('财政收入（亿元）')
plt.plot(data[['y', 'y_pred']], marker='o')  # 画图对比
plt.legend(['财政收入', '财政收入预测值'])  # 指定当前图形的标签
plt.savefig('1.png')  # 保存绘制的图片
plt.show()

结果为：

---

模型评价指标：
采用回归模型评价指标对地方财政收入的预测值进行评价：

from sklearn.metrics import mean_squared_error        # 均方根误差
from sklearn.metrics import mean_absolute_error       # 平均绝对误差
from sklearn.metrics import r2_score                  # 校正决定系数R方值
from sklearn.metrics import mean_squared_log_error    # 均方根对数误差
from sklearn.metrics import median_absolute_error     # 中位数绝对误差
from sklearn.metrics import explained_variance_score  # 解释回归模型的方差得分
import pandas as pd                                   # 导入pandas模块

data = pd.read_excel('new_reg_data_GM11_revenue.xls')  # 读取数据
y_test = data.loc[0:19, 'y']                          # 已有测试值
y_predict = data.loc[0:19, 'y_pred']                  # 预测值
print('平均绝对误差:', mean_absolute_error(y_test, y_predict))
print('均方根误差:', mean_squared_error(y_test, y_predict))
print('校正决定系数:', r2_score(y_test, y_predict))
print('均方根对数误差:', mean_squared_log_error(y_test, y_predict))
print('中位数绝对误差:', median_absolute_error(y_test, y_predict))
print('解释回归模型的方差得分:', explained_variance_score(y_test, y_predict))
# 平均绝对误差: 34.27441608673626
# 均方根误差: 3251.333034114142
# 校正决定系数: 0.990779799573139
# 均方根对数误差: 0.02880077518000288
# 中位数绝对误差: 18.784616662693224
# 解释回归模型的方差得分: 0.9907862002416017

可以看出平均绝对误差与中位数绝对误差较小，解释回归模型的方差得分与R方值接近于1，表明建立的支持向量回归模型拟合效果优良，模型可以用于预测。