旷视2019CVPR-Multi-Label Image Recognition with Graph Convolutional Networks
文章目录
- Multi-Label Image Recognition with Graph Convolutional Networks
- 导语
- 介绍
- 方法
- 动机
- 图卷积网络简介
- 用于多标签识别的GCN
- 相关系数矩阵
- 实验
- MS-COCO实验结果
- VOC 2007实验结果
- 结论
- 开源地址
Multi-Label Image Recognition with Graph Convolutional Networks
转载自旷视南京研究院 https://zhuanlan.zhihu.com/p/62212910
导语
多标签图像识别(multi-label image recognition)任务的目标是预测一张图像中出现的多个物体标签,其在搜索引擎、推荐系统中应用广泛,长期以来作为计算机视觉和机器学习领域一项基础研究课题备受学界业界关注。由于多个相关物体通常同时出现在一副图像之中,因此提升识别性能的一个理想方法就是针对多标记识别的核心问题,即“如何有效建模标记间的协同关系”进行探索,对标签之间的依赖性进行有效建模。
为获取和利用这种依赖性,旷视研究院提出一种基于图卷积网络(Graph Convolutional Network,GCN)的多标签分类模型。该模型通过 data-driven 方式建立标记间有向图(directed graph)并由 GCN 将类别标记映射(mapping)为对应类别分类器,以此建模类别关系,同时可提升表示学习能力。
此外针对 GCN 中的关键元素 correlation matrix 进行了深入分析和重设计,使其更胜任多标记问题。在两个多标签图像识别权威数据集上的实验结果显示,ML-GCN 明显优于目前所有的最佳方法。另外,可视化结果显示,模型习得的分类器还能保持有意义的语义拓扑结构。
介绍
多标签图像识别是计算机视觉领域的一项基本任务,其目标是识别图像中存在的一系列对象。这项技术可应用于医学诊断识别、人类属性识别和零售识别等诸多领域。相比于多类别图像分类,多标签任务的难度更大,因为其输出空间随着类别数目呈指数增大。

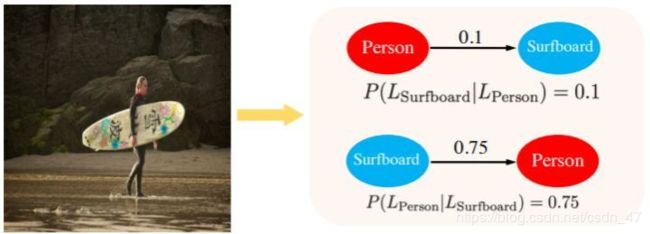
由于现实世界中很多物体通常会同时出现,因此对标签之间的相关性进行建模就成了多标签图像识别的关键,如图 1 所示。
解决多标签识别问题的一个朴素方法是分离地看待各个目标,通过将多标签问题转换成多组二值分类问题,预测每个目标是否存在。由于深度卷积神经网络在单标签图像分类上取得的巨大成功,二值分类的性能已得到极大提升。
但是这些方法忽视了物体之间复杂的拓扑结构,因此在本质上有局限性。正是这个缺陷促使研究员寻找能够获取并从多个角度探索标签之间相关性的方法。其中的部分方法基于概率图模型或循环神经网络(RNN),可显式地对标签依赖性进行建模。
另一个研究方向是通过注意力机制来对标签相关性进行隐式建模。该方法考虑的是图像中被注意区域之间的关系(可视为局部相关性)。不过即便如此,该方法还是忽略了图像中标签之间的全局相关性(全局相关性需要通过单张图像之外的知识才能推断出来)。
为此,旷视研究院提出基于图卷积网络(GCN)的全新模型,即 ML-GCN(Multi-Label Graph Convolutional Network),用于建立多标签之间的相关性,该方法有其它方法无法具备的扩展性和灵活性。
除了将目标分类器视为一组待学习的独立参数向量外,旷视研究院还提出一种可从标签的先验特征(如词嵌入向量)学习相互依赖的目标分类器方法,它通过一个基于 GCN 的映射函数来实现。随后,生成的分类器再被应用于由另一个子网络生成的图像特征,以实现端到端训练。
由于这些从词嵌入向量到分类器的映射参数是在所有类别(如图像标签)之间共享,因此来自所有分类器的梯度都会影响这个基于 GCN 的分类器生成函数。这可以对标签的相关性进行隐式建模。此外,由于分类器的学习涉及到对标签相关性的建模,因此本文设计了一个有效的标签相关系数矩阵,来引导信息在 GCN 各个节点之间的传递。
方法
本节将介绍这一新提出的多标签图像识别模型 ML-GCN。首先是这一方法的动机,接着是一些图卷积网络初步知识,最后是 ML-GCN 模型以及用于相关系数矩阵构建的二次加权方法。
动机
如何有效获取目标标签之间的相关性?如何利用这些标签相关性提升分类表现?这是多标签图像识别的两个重要问题。本文使用图(graph)来对标签之间的相互依赖关系进行建模。这种方法能够灵活地获取标签空间中的拓扑结构。
旷视研究员将图中的每个节点(标签)都表示为该标签的词嵌入向量,并提出使用 GCN 直接将词嵌入向量映射到一组互相依赖的分类器上,这些分类器进一步又可直接应用于图像特征以进行分类。基于 GCN 的模型有两个设计动机:
- 由于从词嵌入向量到分类器的映射参数在所有类别中是共享的,所以习得的分类器能够在词嵌入空间中(语义相关的概念在词嵌入空间中彼此临近)保留较弱的语义结构。与此同时,对于可以对标签依赖性进行隐式建模的分类器函数,所有分类器的梯度都会对它产生影响。
- 基于标签的共现模式,旷视研究员设计了一个全新的标签相关系数矩阵,可显式地用 GCN建模标签相关性,让节点的特征在更新时也能从相关联的节点(标签)吸收信息。
图卷积网络简介
图卷积网络可用于进行半监督分类任务,其核心思想是通过节点之间的信息传播来更新节点的表示。
不同于在一张图像局部欧氏结构之上进行操作的标准卷积方法,GCN 的目标是学习一个图 G的函数 f ( . , . ) f(., .) f(.,.)。该函数的输入是特征描述 H l ∈ R h × d H^{l}\in\mathbb{R}^{h\times d} Hl∈Rh×d和相关系数矩阵 A ∈ R n × n A\in \mathbb{R}^{ n\times n} A∈Rn×n ,从而把节点特征更新为 H l + 1 ∈ R n × d ′ H^{l+1}\in\mathbb{R}^{n\times d^{'}} Hl+1∈Rn×d′。每个 GCN 层都可以写成一个非线性函数:
H l + 1 = f ( H l , A ) \boldsymbol { H } ^ { l + 1 } = f \left( \boldsymbol { H } ^ { l } , \boldsymbol { A } \right) Hl+1=f(Hl,A)
f (., .) 可以表示为:
H l + 1 = h ( A ^ H l W l ) \boldsymbol { H } ^ { l + 1 } = h \left( \widehat { \boldsymbol { A } } \boldsymbol { H } ^ { l } \boldsymbol { W } ^ { l } \right) Hl+1=h(A HlWl)
如此一来,便可以通过堆叠多个 GCN 层来对节点之间交织的复杂关系进行建模。
用于多标签识别的GCN
GCN 的设计初衷是半监督分类,其节点层面的输出结果是每个节点的预测分数。不同的是,在 ML-GCN 中,每个 GCN 节点的最终输出都被设计成与标签相关的分类器。此外,不同于其它任务,这里的多标签图像分类任务没有提供预定义的图结构(即相关系数矩阵)。这需要从头构建相关系数矩阵。
图 2 展示了该方法的整体架构,它包含两个主要模块:图像特征学习模块和基于 GCN 的分类器学习模块。

图像特征学习:原则上可使用任意基于 CNN 的模型学习图像特征。本文在实验中使用 ResNet-101 作为实验基础模型;然后应用 全局最大池化 获取图像层面的特征 x:
x = f G M P ( f c n n ( I ; θ c n n ) ) ∈ R D \boldsymbol { x } = f _ { \mathrm { GMP } } \left( f _ { \mathrm { cnn } } \left( \boldsymbol { I } ; \theta _ { \mathrm { cnn } } \right) \right) \in \mathbb { R } ^ { D } x=fGMP(fcnn(I;θcnn))∈RD
GCN 分类器学习:通过一个基于 GCN 的映射函数从标签特征学习相互依赖的目标分类器
W = { w i } i = 1 C \boldsymbol { W } = \left\{ \boldsymbol { w } _ { i } \right\} _ { i = 1 } ^ { C } W={wi}i=1C
旷视研究员使用堆叠 GCN,其中每个 GCN 层 I 的输入都取前一层 H l H^{l} Hl的节点特征作为输入,然后输出新的节点特征 H l + 1 H^{l+1} Hl+1。第一层的输入是词嵌入向量
Z ∈ R C × d Z \in \mathbb { R } ^ { C \times d } Z∈RC×d
通过将所学到的分类器应用于图像特征,得到预测分数:
y ^ = W x \hat { \boldsymbol { y } } = \boldsymbol { W } \boldsymbol { x } y^=Wx
假设一张图像的真实标签是
y ∈ R C y \in \mathbb { R } ^ { C } y∈RC
那么整个网络可使用传统多标签分类的损失函数来训练,如下:
L = ∑ c = 1 C y c log ( σ ( y ^ c ) ) + ( 1 − y c ) log ( 1 − σ ( y ^ c ) ) \mathcal { L } = \sum _ { c = 1 } ^ { C } y ^ { c } \log \left( \sigma \left( \hat { y } ^ { c } \right) \right) + \left( 1 - y ^ { c } \right) \log \left( 1 - \sigma \left( \hat { y } ^ { c } \right) \right) L=c=1∑Cyclog(σ(y^c))+(1−yc)log(1−σ(y^c))
相关系数矩阵
基于相关系数矩阵,GCN 可在节点之间进行信息传递,因此如何构建相关系数矩阵 A 就成了GCN 模型中一个非常重要的问题。旷视研究员在本文中以数据驱动的方式构建了一个相关系数矩阵,换句话说,相关性可以通过挖掘标签在数据集中的共现模式而来定义。
本文以条件概率的形式(即
P ( L j ∣ L i ) P \left( L _ { j } | L _ { i } \right) P(Lj∣Li)
P ( L j ∣ L i ) P \left( L _ { j } | L _ { i } \right) P(Lj∣Li)
为构建相关系数矩阵,本文首先统计了训练数据集中标签对的出现次数,得到矩阵
M ∈ R C × C M \in \mathbb { R } ^ { C \times C } M∈RC×C
然后使用这个标签共现矩阵得到条件概率矩阵:
P i = M i / N i \boldsymbol { P } _ { i } = \boldsymbol { M } _ { i } / N _ { i } Pi=Mi/Ni
然而,上面这种简单的相关性可能有两个缺陷。首先,一个标签和其它标签的共现模式可能表现为长尾分布,其中某些罕见的共现可能是噪声;其次,训练和测试中共现的绝对数可能并不完全一致。因此,本文提出对相关系数矩阵进行二值化处理。具体而言,研究人员将阈值用于过滤噪声边,其中 A 是二值相关系数矩阵
A i j = { 0 , if P i j < τ 1 , if P i j ≥ τ A _ { i j } = \left\{ \begin{array} { l l } { 0 , } & { \text { if } P _ { i j } < \tau } \\ { 1 , } & { \text { if } P _ { i j } \geq \tau } \end{array} \right. Aij={0,1, if Pij<τ if Pij≥τ
过度平滑问题(我不是很懂):根据 (2) 式可以知道,经过 GCN 后,一个节点的特征是其自身特征和相邻节点特征的加权和。而二值化相关系数矩阵的一个直接问题是其可能导致过度平滑。为了缓解这一问题,本文提出以下二次加权方法:
A i j ′ = { p / ∑ j = 1 i ≠ j C A i j , if i ≠ j 1 − p , if i = j \boldsymbol { A } _ { i j } ^ { \prime } = \left\{ \begin{array} { l l } { p / \sum _ { j = 1 \atop i \neq j } ^ { C } \boldsymbol { A } _ { i j } , } & { \text { if } i \neq j } \\ { 1 - p , } & { \text { if } i = j } \end{array} \right. Aij′={p/∑i̸=jj=1CAij,1−p, if i̸=j if i=j
通过这种做法,在更新节点特征时,节点本身的权重是固定的,相关节点的权重则由邻近分布确定。当 p→1 时,不考虑节点本身的特征;当 p→0 时,往往忽略相邻信息。
实验
多标签图像识别基准数据集 MS-COCO 和 VOC 2007 上的实验结果表明,本文方法实现当前最优。
MS-COCO实验结果
对于 ML-GCN,旷视研究员给出了基于二值相关系数矩阵与基于二次加权相关系数矩阵两个版本的结果,后者的分类表现更好,可以有效缓解上述问题,从而在几乎所有指标上领先其它方法,这证明了新提出的网络与二次加权法的有效性。具体实验结果见表 1。

VOC 2007实验结果
为公平对比,旷视研究员给出了以 VGG 为基本模型的结果。由表 2 可知,使用权重更新方案的 ML-GCN 模型在 mAP 指标上得到 94% 的分数,高出先前最优方法 2%。此外,即使以 VGG 为基础模型,仍然超出先前最佳水平 0.8%。

结论
标签相关性建模是多标签图像识别的一大关键问题。为建模和利用这种重要信息,旷视研究院提出基于 GCN 的模型来根据先验的标签特征(比如词嵌入向量)学习互相依赖的目标分类器。
为了对标签相关性进行显式建模,文中设计了一种全新的二次加权方法,可通过平衡节点与其相邻节点来为 GCN 构建一个相关系数矩阵,以更新节点特征,从而有效缓解了妨碍 GCN 性能的两大问题:过拟合与过度平滑。定量和定性实验结果都表明新方法的优越性。
开源地址
https://github.com/chenzhaomin123/ML_GCN