算法岗常见面试题
文章目录
- 深度学习
- 1.讲一讲faster_rcnn
- 2.你了解哪些激活函数?分别有什么用?
- 3.批梯度下降、随机梯度下降和mini-batch梯度下降的区别?
- 4.CNN里有哪些常见的梯度下降方法?
- 5.池化层是怎样进行反向传播的?
- 6.深度学习不适合哪些应用场景?
- 7.浅层神经网络和深层神经网络的差别?
- 8.什么是过拟合?防止过拟合的方法?
- 9.为什么负梯度方向是函数局部值最快的方向?
- 10.为什么图像处理中一般用最大池化而不用平均池化?
- 11.softmax loss和cross entropy的区别?
- 12.全连接层的作用
- 13.训练不收敛(loss不下降)怎么办?
- 14.怎么计算感受野(receptive field)?
- 15.详细介绍一下Batch Normalization(怎么计算均值、方差,怎么反向传播等)
- 16.RNN和LSTM有什么不同?
- RNN:
- LSTM:
- 17. 为什么RNN不用Relu函数而要用tanh函数?
- 18.写一下卷积的实现
- 19.空洞卷积的思想?或者说相比如标准卷积有什么改进?
- 机器学习
- 1.介绍一下线性回归
- 2.推导一下逻辑回归(LR)
- 3.偏差与方差
- 4.介绍一下SVM
- 5.讲一讲PCA(SVD)
- 6.数据不均衡怎么办?
- 7.有哪些经典的聚类算法?
- 8. 归一化的好处?哪些模型需要归一化?
- 10. k-measn的k值如何确定?
- 11. KNN的k值选取方法的k值大小的影响?
- 12. GBDT和XGBoost的区别?
- 13.XGboost的损失函数?XGBoost哪些参数可以用来防止过拟合?
- 14.XGBoost和LightGBM的区别?
- 15.特征选择方法有哪些?
- 16.XGBoost和Random Forest单棵树谁的深度更深?
- 图像处理
- 1.图像处理的知识
- 2.传统的特征提取方法有哪些?
- 3.两个图像库,场景一一对应,一个有雨滴,一个没有雨滴,对有雨滴的图像去除雨滴,要不留痕迹。
- 数据结构/算法
- 1.会写红黑树吗?
- 2.复习一下排序算法。
- 3.散列表解决冲突的方法有哪些?
- 4.二叉树的递归遍历和非递归遍历
- 5.KMP算法
- 操作系统/计算机网络/数据库
- 1.进程和线程的区别?
- 2.什么是死锁?产生的原因?必要条件?解决办法?
- 3.进程间的通信?
- 4.线程间的通信方式?
- 5.TCP传输为什么可靠(TCP是怎么实现可靠传输的)?
- 6. 拥塞控制
- 7.TCP和UDP有什么区别?
- 8. 为什么TCP建立会话要三次握手?
- 9.四次挥手
- Python/C++
- 1.Python中is和==的区别?
- 2.Python中range和xrange的区别?
- 3.Python多线程为什么是鸡肋?
- 4.Python赋值、浅拷贝和深拷贝的区别?
- 5.python传参会改变参数值吗(python是值传递还是引用传递)?
- 6.Python装饰器?
- 7.Python生成器?
- 8.C++的多态是什么?怎么实现的?
- 9.C++中的static、external、register这些关键字
- 10.结构体占多少字节?
- 11.写一下lower_bound和upper_bound的实现。
- 12.指针和引用的区别?
- 13.你用过哪些C++11的特性?
- 14.sizeof和strlen的区别?
- 15.C++中的const关键字。
- 16.了解vector的实现吗?
- 17.getline的用法
- 18.重写与重载的区别?
- 19.define和const的区别?
- 20. 结构和联合的区别?
- 21.C++单例模式了解吗?
- Linux/Spark
- 1.查看进程的命令?
- 2.在linux某个文件中搜索?
- 数学/思维
- 1.一个骰子,6面,1个面是 1, 2个面是2, 3个面是3, 问平均掷多少次能使1,2,3都至少出现一次?
- 2.给10x10的棋盘,扫雷,随机放置10个点作为雷,如何保证随机放置?
- 3.有54张牌,分3组,大王小王同在一组的概率?
- 4.站在地球上的某一点,向南走一公里,然后向东走一公里,最后向北走一公里,回到了原点。地球上有多少个满足这样条件的点?
- 5.一个四位数abcd,满足abcd * 4 = dcba,求这个数。
- 6.一个圆上随机三个点组成锐角三角形的概率?
- 7.100个人坐100个座位,第一个人随机坐,后面每个人如果能做自己的座位就坐自己的座位,不能的话就随机坐,问第100个人坐自己的座位的概率?
- 项目相关
- 1.文字检测项目有什么不错的做法和创新?
- 2.谈谈深度学习发展
- 3.文字检测部分网络用的损失函数是什么?
- 4.推导一下CTC_LOSS
- 5.文字检测和识别你还看过哪些论文?
- 6.半自然驾驶数据集项目碰到的最大困难?
- 7.半自然驾驶数据集项目中数据主要分析过程
- 8.除了softmax还有哪些方法可以把数值转换成概率?
- 9.多卡训练时的梯度更新过程?
- 10.目标检测中如果目标是倒着的怎么办?
- 11.GCN的损失函数?
- HR面
- 1.做一下自我介绍
- 2.你未来的职业规划是什么?(做研究?做业务?做平台?)
- 3.你研究生生涯遇到的最大挑战是什么?怎么解决的?
- 4.你最骄傲/自豪的事情是什么?
深度学习
1.讲一讲faster_rcnn
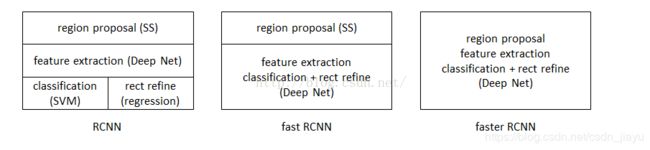
首先从rcnn讲起,rcnn可以称得上是用深度学习进行目标检测的开山之作。其方法是首先用Selective Search算法选出约2000-3000个候选区域(region proposal),然后将这些区域图块归一化成227*227的图像,再通过CNN提取特征,得到4096维的特征。接下来分为两步:对上面每一个区域得到的特征都用一个二分类SVM分类器判断候选区域是否是目标(在SVM中正负样本数差别悬殊,可通过增大数量少的样本的C值来增大“少数样本误分类”带来的影响,避免被多数样本掩盖);如果候选区域属于某个类别,用线性脊回归器对该候选进行位置精修。
详见博客:【目标检测】RCNN算法详解
Fast RCNN
RCNN主要存在三个问题:
- 训练时速度慢
- 测试时速度慢
- 训练所需空间大
Fast RCNN分别针对这三个问题进行了改进:
- RCNN训练时速度慢是因为对每一个候选框都要使用CNN进行特征提取,而各个候选框之间大量重叠,因此造成大量冗余计算。而Fast RCNN先将一整张图片送入网络,然后再送入候选区域,因此前几层不需要再重复计算,提高了计算速度。
- RCNN测试时速度慢原因同上,而Fast RCNN将一整张图归一化后送入网络,在邻接时才送入候选框,只需要在后基层处理候选框就行。
- RCNN中分类器和回归器都需要大量的特征作为训练数据,而Fast RCNN统一用深度学习网络进行类别估计和位置精修,不需要额外存储。
总的来说,Fast RCNN的的流程就是先将图片归一化为224*224大小,然后用基础网络提取特征,在基础网络的输出层加入候选区域(例如VGG16就是在最后一层池化层加入候选区域,将每个候选区域均匀分成M*N块,再用max_pool将候选区域调整到大小一致,再送入下一层),通过全连接层得到4096维的数据。在用多任务学习,同时学习候选区域是否属于某一类以及对照该类的标签框精修候选区域位置。
详情参见:【目标检测】Fast RCNN算法详解
** Faster RCNN**
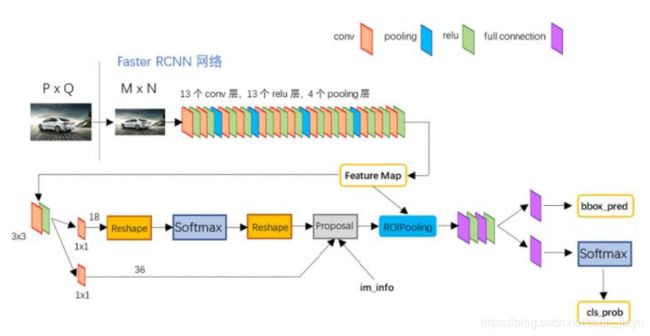
主要解释Proposal层:
- 生成anchors,利用bbox_regression分支得到的(tx, ty, tw, th)参数对anchors进行修正。
- 对anchors按foreground_softmax_scores从高到低进行排序,取top_n(eg: 6000)的留下,从而获得修正后的positive_anchors
- 对超出边界的positive_anchors进行修剪
- 剔除太小的positive_anchors
- nms
- 对nms后的positive_anchors再次按foreground_softmax_scores从高到低排序,留下top_n(eg: 300)的positive_anchors。
- 现在还留下的anchors就是proposals
详见:一文读懂Faster RCNN
2.你了解哪些激活函数?分别有什么用?
激活函数的主要作用是引入非线性变换,如果没有激活函数的话,神经网络层数再多,也只是简单的线性变换,无法处理图像、语音等复杂的任务。
1.阶跃函数
用于二分类,但导数始终为0,不能用于反向传播,理论意义大于实际意义。
2.sigmoid函数
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
同样用于二分类,X靠近0的时候,一点小小的值变化也能引起Y的很大变化,这说明函数区域将数值推向极值,很适合二分类。而X远离0的时候,X值变化对Y起作用很小,函数的导数变化也很小,在反向传播中几乎起不到更新梯度的作用;且sigmoid函数只能得到正值,在很多情况下不适用。
3.tanh函数
f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} f(x)=ex+e−xex−e−x
对sigmoid函数的改进,函数值在(-1, 1)之间,改善了sigmoid函数只能得到正值的缺点,其他特点与sigmoid函数一模一样。
4.ReLU函数
ReLU函数是近年来神经网络使用最广泛的激活函数,它的一大优点就是当输入值是负值的时候,输出值为0,这意味着一段时间内只有部分神经元被激活,神经网络的这种稀疏性使其变得高效且易于计算。但X小于0时函数的梯度为0,这就意味着在反向传播的时候权重得不到更新,那么正想传播过程中输出值为0的神经元永远得不到激活,变成了死神经元。
5.Leaky ReLU函数
解决了死神经元的问题。
6.Softmax函数
Softmax函数也可以看作是用作多分类的激活函数,将神经网络的输出值编程概率。
此外还有线性激活函数,效果等同于未激活,在Keras中不激活时就是用f(x)=x这一激活函数。
二分类时用sigmoid函数和tanh函数,但存在梯度消失问题时应避免使用这两种函数。ReLU函数适用于绝大多数情况,如果存在梯度不更新的问题时可以用Leaky ReLU函数替代。
详见:深度学习基础篇:如何选择正确的激活函数?
3.批梯度下降、随机梯度下降和mini-batch梯度下降的区别?
- 批梯度下降是每次使用所有数据用于更新梯度,使得梯度总是朝着最小的方向更新,但数据量很大的时候更新速度太慢,而且容易陷入局部最优。
- 随机梯度下降是每次使用一条数据来更新梯度,在梯度更新过程中梯度可能上升也可能下降,但总的来说梯度还是朝着最低的方向前进;最后梯度会在极小值附近徘徊。随机梯度下降的梯度更新速度快于批梯度下降,且由于每次梯度的更新方向不确定,陷入局部最优的时候有可能能跳出该局部极小值。
- mini-batch梯度下降介于批梯度下降和随机梯度下降之间,每次用若干条数据更新梯度。mini-batch梯度下降可以使用矩阵的方式来计算梯度,因此速度快于随机梯度下降,且同样具有跳出局部最优的特点。
4.CNN里有哪些常见的梯度下降方法?
这个问题一般是问有哪些优化器
GradientDescent
g t = ▽ f ( θ t − 1 ) △ θ t = − η ∗ g t g_t=\bigtriangledown f(\theta_{t-1})\\ \bigtriangleup \theta_t=-\eta*g_t gt=▽f(θt−1)△θt=−η∗gt
其中 g t g_t gt表示梯度, η \eta η表示学习率。如果算力和时间足够,用SGD训练出的神经网络效果最好。
Momentum
m t = μ ∗ m t − 1 + ( 1 − μ ) g t △ θ t = − η ∗ m t m_t = \mu * m_{t-1}+(1-\mu)g_t\\ \bigtriangleup \theta_t = -\eta * m_t mt=μ∗mt−1+(1−μ)gt△θt=−η∗mt
借用物理学中动量的概念,积累之前的动量代替真正的梯度进行更新。如果本次梯度衰减方向与上一次相同,则可以加速梯度下降;如果不一致,则抑制梯度的改变。
RMSprop
n t = ν n t − 1 + ( 1 − ν ) g t 2 △ θ t = − η n t + ϵ ∗ g t n_t = \nu n_{t-1} + (1-\nu)g_t^2\\ \bigtriangleup \theta_t = -\frac{\eta}{\sqrt{n_t+\epsilon}}*g_t nt=νnt−1+(1−ν)gt2△θt=−nt+ϵη∗gt
用初始学习率除以通过衰减系数控制的梯度平方和的平方根,相当于给每个参数赋予了各自的学习率。梯度相对平缓的地方,累积梯度小,学习率会增大;梯度相对陡峭的地方,累积梯度大,学习率会减小。从而加速训练。
Adam
m t = μ m t − 1 + ( 1 − μ ) g t n t = ν n t − 1 + ( 1 − ν ) g t 2 m t ^ = m t 1 − μ t n t ^ = n t 1 − ν t △ θ t = − η n t ^ + ϵ ∗ m t ^ m_t = \mu m_{t-1} + (1-\mu)g_t\\ n_t = \nu n_{t-1} + (1-\nu)g_t^2\\ \hat {m_t} = \frac{m_t}{1-\mu^t}\\ \hat {n_t} = \frac{n_t}{1-\nu^t}\\ \bigtriangleup \theta_t = -\frac{\eta}{\sqrt{\hat {n_t}+\epsilon}}*\hat {m_t} mt=μmt−1+(1−μ)gtnt=νnt−1+(1−ν)gt2mt^=1−μtmtnt^=1−νtnt△θt=−nt^+ϵη∗mt^
Adam本质上是带有动量项的RMSprop,结合了两者的优点,可以为不同的参数计算不同的自适应学习率,在实践中一般都用Adam优化器。
详见:深度学习最全优化方法总结比较(SGD,Adagrad,Adadelta,Adam,Adamax,Nadam)
5.池化层是怎样进行反向传播的?
反向传播在经过池化层的时候梯度的数量发生了变化,例如对于2*2的池化操作,第L+1层梯度数量是L层的1/4,所以每个梯度要对应回4个梯度,而这对于mean_pooling和max_pooling来说存在区别。
mean_pooling

由于mean_pooling正向传播时取周围4个像素的均值,所以反向传播将梯度平均分成4分,再分给上一层。
max_pooling
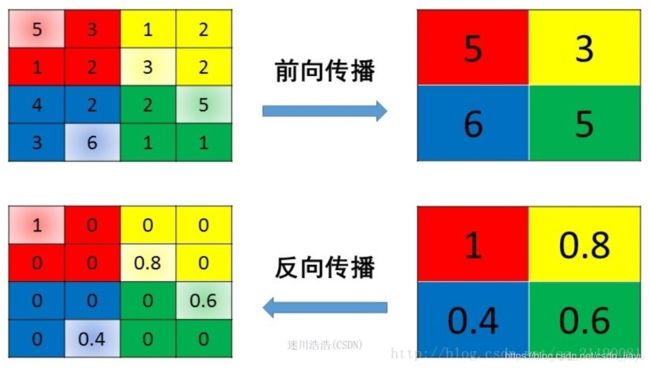
max_pooling正向传播时取周围4个像素的最大值保留,其余的值丢弃,所以反向传播时将梯度对应回最大值的位置,其他位置取0。一般来说,为了知道最大值的位置,深度学习框架在正向传播时就用max_id来记录4个像素中最大值的位置。
详见博客:深度学习笔记(3)——CNN中一些特殊环节的反向传播
6.深度学习不适合哪些应用场景?
- 日常生活的预测问题或生物学中的小样本问题:在这些问题中使用线性模型往往能比深度学习效果更好,而且速度更快。
- 需要知道变量与结果之间的关系,而不是仅仅给出一个预测值的时候。例如,医生想要知道人口变量对死亡率的影响,这个时候深度学习就不适合。
- 非结构化数据中深度学习不适合。
详见博客:深度学习的先入之见、局限性及其未来
7.浅层神经网络和深层神经网络的差别?
神经网络中,权重参数是给数据做线性变换,而激活函数给数据带来的非线性变换。增加某一层神经元数量是在增加线性变换的复杂性,而增加网络层数是在增加非线性变换的复杂性。
理论上来说,浅层神经网络就能模拟任何函数,但需要巨大的数据量,而深层神经网络可以用更少的数据量来学习到更好的拟合。
8.什么是过拟合?防止过拟合的方法?
过拟合是模型学习能力太过强大,把部分数据的不太一般的特性都学到了,并当成了整个样本空间的特性。在深度学习中主要有以下几个方法防止过拟合:
- L2正则化
原loss是 L 0 L_0 L0,加入L2正则化后loss是 L = L 0 + λ 2 n ∣ ∣ W ∣ ∣ 2 L=L_0+\frac{\lambda}{2n}||W||^2 L=L0+2nλ∣∣W∣∣2
所以L的梯度是 ∂ L ∂ W = ∂ L 0 ∂ W + λ n W \frac{\partial{L}}{\partial{W}}=\frac{\partial{L_0}}{\partial{W}}+\frac{\lambda}{n}{W} ∂W∂L=∂W∂L0+nλW
∂ L ∂ b = ∂ L 0 ∂ b \frac{\partial{L}}{\partial{b}}=\frac{\partial{L_0}}{\partial{b}} ∂b∂L=∂b∂L0
可以看出,L2正则化只对W有影响,对b没有影响。而加入L2正则化后的梯度更新:
W = W − α ( ∂ L 0 ∂ W + λ n W ) = ( 1 − α λ n ) W − α ∂ L 0 ∂ W W=W-\alpha(\frac{\partial{L_0}}{\partial{W}}+\frac{\lambda}{n}{W})=(1-\frac{\alpha\lambda}{n})W-\alpha\frac{\partial{L_0}}{\partial{W}} W=W−α(∂W∂L0+nλW)=(1−nαλ)W−α∂W∂L0
相比于原梯度更新公式,改变的是 ( 1 − 2 α λ ) W (1-2\alpha\lambda)W (1−2αλ)W这里,而由于 α 、 λ 、 n \alpha、\lambda、n α、λ、n都是正数,所以 ( 1 − α λ n ) < 1 (1-\frac{\alpha\lambda}{n})<1 (1−nαλ)<1。
因此,L2正则化使得反向传播更新参数时W参数比不添加正则项更小。在过拟合中,由于对每个数据都拟合得很好,所以函数的变化在小范围内往往很剧烈,而要使函数在小范围内剧烈变化,就是要W参数值很大。L2正则化抑制了这种小范围剧烈变化,使得拟合程度“刚刚好”。 - L1正则化
原loss是 L 0 L_0 L0,加入L1正则化后loss是 L = L 0 + λ n ∣ W ∣ L=L_0+\frac{\lambda}{n}|W| L=L0+nλ∣W∣
所以L的梯度是 ∂ L ∂ W = ∂ L 0 ∂ W + λ n ∣ W ∣ \frac{\partial{L}}{\partial{W}}=\frac{\partial{L_0}}{\partial{W}}+\frac{\lambda}{n}|W| ∂W∂L=∂W∂L0+nλ∣W∣
∂ L ∂ b = ∂ L 0 ∂ b \frac{\partial{L}}{\partial{b}}=\frac{\partial{L_0}}{\partial{b}} ∂b∂L=∂b∂L0
可以看出,L2正则化只对W有影响,对b没有影响。而加入L2正则化后的梯度更新:
W = W − α ( ∂ L 0 ∂ W + λ n ∣ W ∣ ) = W − λ n ∣ W ∣ − α ∂ L 0 ∂ W W=W-\alpha(\frac{\partial{L_0}}{\partial{W}}+\frac{\lambda}{n}{|W|})=W-\frac{\lambda}{n}|W|-\alpha\frac{\partial{L_0}}{\partial{W}} W=W−α(∂W∂L0+nλ∣W∣)=W−nλ∣W∣−α∂W∂L0
如果W为正,相对于原梯度就减小;如W为负,相对于原梯度就增大。
所以,L1正则化使得参数W在更新时向0靠近使得参数W具有稀疏性。而权重趋近0,也就相当于减小了网络复杂度,防止过拟合。 - Dropout
Dropout在每次训练时,有一部分神经元不参与更新,而且每次不参与更新的神经元是随机的。随着训练的进行,每次用神经元就能拟合出较好的效果,少数拟合效果不好的也不会对结果造成太大的影响。 - 增大数据量
既然过拟合是学习到了部分数据集的特有特征,那么增大数据集就能有效的防止这种情况出现。 - Early stop
数据分为训练集、验证集和测试集,每个epoch后都用验证集验证一下,如果随着训练的进行训练集loss持续下降,而验证集loss先下降后上升,说明出现了过拟合,应该立即停止训练。 - Batch Normalization(下面另有BN的详细过程,见问题21)
BN的过程中,每次都是用一个mini_batch的数据来计算均值和反差,这与整体的均值和方差存在一定偏差,从而带来了随机噪声,起到了与Dropout类似的效果,从而减轻过拟合。
详见博客:正则化方法:L1和L2 regularization、数据集扩增、dropout
9.为什么负梯度方向是函数局部值最快的方向?
假设存在函数 f ( x ) f(x) f(x), l l l是任意方向的单位向量,要现在的目的就是要找到一个 l l l使得 f ( x + l ) − f ( x ) f(x+l)-f(x) f(x+l)−f(x)的变化值最大。
根据公式有 f ( x + l ) − f ( x ) = < g r a d f , l > f(x+l)-f(x)=
详见博客:在梯度下降法中,为什么梯度的负方向是函数下降最快的方向?
10.为什么图像处理中一般用最大池化而不用平均池化?
池化的主要目的有两个:(1)保持主要特征不变的同时减小了参数(2)保持平移、旋转、尺度不变性,增强了神经网络的鲁棒性
详见:如何理解CNN中的池化?
而之所以用最大池化而不用平均池化,主要原因是最大池化更能捕捉图像上的变化、梯度的变化,带来更大的局部信息差异化,从而更好地捕捉边缘、纹理等特征。
11.softmax loss和cross entropy的区别?
输入数据经过神经网络后得到的logits是一个[n, 1]向量(n表示进行n分类),此时向量中的数字可以是负无穷到正无穷的任意数字,经过softmax函数后才转换为概率。
softmax函数:
P i = e i ∑ k = 1 n e k P_i=\frac{e^i}{\sum_{k=1}^{n}e^k} Pi=∑k=1nekei
softmax loss:
L = − ∑ i = 1 n y i l o g p i L=-\sum_{i=1}^{n}y_ilogp_i L=−i=1∑nyilogpi
cross entropy:
L = − ∑ i = 1 n y i l o g p i L=-\sum_{i=1}^{n}y_ilogp_i L=−i=1∑nyilogpi
交叉熵函数形式与softmax loss函数几乎一样,当cross entropy的输入是softmax函数函数的输出时,二者就完全一样。
最后看一下logistic regression函数:
L = − y i l o g p i − ( 1 − y i ) l o g ( 1 − p i ) L=-y_ilogp_i-(1-y_i)log(1-p_i) L=−yilogpi−(1−yi)log(1−pi)
12.全连接层的作用
全连接层的作用主要是“分类”,将卷积层提取到的特征进行维数调整,同时融合各通道之间的信息。
还有一个作用就是在迁移学习的过程中,有全连接层的模型比没有全连接层的表现更好。
详见博客:全连接层的作用是什么? - 魏秀参的回答 - 知乎
13.训练不收敛(loss不下降)怎么办?
(1)首先检查是否进行了数据归一化
(2)网络的输出层是否用了正确的激活函数(如果最后一层是回归,最好不要用激活函数)
(3)调整学习率试试
(4)仔细检查自己定义的网络层是否有错误
(5)检查loss是否有错误
(6)调整batch_size试试
(6)如果还不行,试试只用几张图片,去除正则化等优化手段,看是否能过拟合。不能的话可能是网络结构有问题,仔细检查代码是否错误,以及调整网络结构试试。
(7)另外:善用tensorboard可视化训练过程
详见:神经网络不学习的原因
14.怎么计算感受野(receptive field)?
感受野指的是当前层每一个特征对应输入图的区域大小。假设输入特征时5*5特征图(下图中蓝色方块区域),采用kernel_size=3,padding=1, stride=2的方式连续进行两次卷积。第一次卷积后得到3*3特征图(绿色方块区域),再次卷积后得到2*2特征图(橙色方块区域)。下图左列是我们常见的特征图可视化方式,右列是固定大小特征图可视化方式,我们根据固定大小特征图计算感受野。
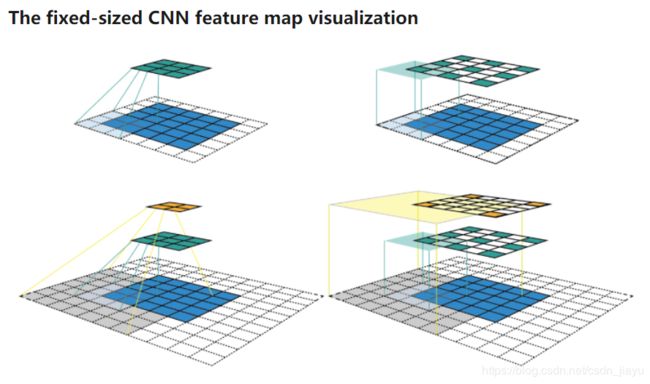
首先定义几个参数: j j j表示在固定两个特征之间的距离, r r r表示感受野大小, s s s表示stride大小, k k k表示kernel_size。
第一次卷积前后:
j o u t = j i n ∗ s = 1 ∗ 2 = 2 j_{out}=j_{in}*s=1*2=2 jout=jin∗s=1∗2=2
r o u t = r i n + ( k − 1 ) ∗ j i n = 1 + ( 3 − 1 ) ∗ 1 = 3 r_{out}=r_{in}+(k-1)*j_{in}=1+(3-1)*1=3 rout=rin+(k−1)∗jin=1+(3−1)∗1=3
所以第一次卷积后感受野大小为3.
第二次卷积前后(上一层的 j o u t 、 r o u t j_{out}、r_{out} jout、rout作为这一层的 j i n 、 r i n j_{in}、r_{in} jin、rin):
j o u t = j i n ∗ s = 2 ∗ 2 = 4 r o u t = r i n + ( k − 1 ) ∗ j i n = 3 + ( 3 − 1 ) ∗ 2 = 7 j_{out}=j_{in}*s=2*2=4\\ r_{out}=r_{in}+(k-1)*j_{in}=3+(3-1)*2=7 jout=jin∗s=2∗2=4rout=rin+(k−1)∗jin=3+(3−1)∗2=7
因此本例中两次卷积后橙色区域特征图感受野为7*7。
15.详细介绍一下Batch Normalization(怎么计算均值、方差,怎么反向传播等)
神经网络反向传播后每一层的参数都会发生变化,在下一轮正向传播时第 l l l层的输出值 Z l = W ⋅ A l − 1 + b Z^l=W\cdot{A}^{l-1}+b Zl=W⋅Al−1+b也会发生变化,从而导致第 l l l层的 A l = r e l u ( Z l ) A^l=relu(Z^l) Al=relu(Zl)发生变化。而 A l A^l Al作为第 l + 1 l+1 l+1层的输入, l + 1 l+1 l+1就需要去适应适应这种数据分布的变化,这就是神经网络难以训练的原因之一。
为此,Batch Normalization的做法是调整数据的分布来改变这一现象,具体做法如下:
-
训练
训练过程中,一般每次的训练数据都是一个batch,假设 m = b a t c h _ s i z e m=batch\_size m=batch_size,则:
(1)计算各个特征均值 μ = 1 m ∑ i = 1 m z i \mu=\frac{1}{m}\sum_{i=1}^{m}z^i μ=m1∑i=1mzi,其中 z i z^i zi表示第 i i i条数据
(2)计算方差 σ 2 = 1 m ∑ i = 1 m ( z i − μ ) 2 \sigma^2=\frac{1}{m}\sum_{i=1}^{m}(z^i-\mu)^2 σ2=m1∑i=1m(zi−μ)2
(3)归一化后的 Z n o r m i = z i − μ σ 2 + ϵ Z_{norm}^i=\frac{z^i-\mu}{\sqrt{\sigma^2+\epsilon}} Znormi=σ2+ϵzi−μ, ϵ \epsilon ϵ表示一个极小值,防止计算出现Nan。
(4)这样调整分布后能加速训练,但之前层学习到的参数信息可能会丢失,所以加入参数 γ 、 β \gamma、\beta γ、β进行调整: Z ~ i = γ Z n o r m i + β \widetilde{Z}^i=\gamma{Z_{norm}^i}+\beta Z i=γZnormi+β -
反向传播
∂ L ∂ Z n o r m i = ∂ L ∂ Z ~ i λ \frac{\partial{L}}{\partial{Z_{norm}^i}}=\frac{\partial{L}}{\partial{\widetilde{Z}^i}}\lambda ∂Znormi∂L=∂Z i∂Lλ
∂ L ∂ λ = ∂ L ∂ Z ~ i Z n o r m i \frac{\partial{L}}{\partial\lambda}=\frac{\partial{L}}{\partial{\widetilde{Z}^i}}Z_{norm}^i ∂λ∂L=∂Z i∂LZnormi
∂ L ∂ β = ∂ L ∂ Z ~ i \frac{\partial{L}}{\partial\beta}=\frac{\partial{L}}{\partial{\widetilde{Z}^i}} ∂β∂L=∂Z i∂L
∂ L ∂ σ 2 = ∂ L ∂ Z n o r m i ∂ Z n o r m i ∂ σ 2 = ∂ L ∂ Z n o r m i ( − 1 2 ) ( σ 2 + ϵ ) − 3 2 \frac{\partial{L}}{\partial\sigma^2}=\frac{\partial{L}}{\partial{Z_{norm}^i}}\frac{\partial{Z_{norm}^i}}{\partial\sigma^2}=\frac{\partial{L}}{\partial{Z_{norm}^i}}(-\frac{1}{2})(\sigma^2+\epsilon)^{\frac{-3}{2}} ∂σ2∂L=∂Znormi∂L∂σ2∂Znormi=∂Znormi∂L(−21)(σ2+ϵ)2−3
∂ L ∂ μ = ∂ L ∂ Z n o r m i ∂ Z n o r m i ∂ μ + ∂ L ∂ σ 2 ∂ σ 2 ∂ μ \frac{\partial{L}}{\partial\mu}=\frac{\partial{L}}{\partial{Z_{norm}^i}}\frac{\partial{Z_{norm}^i}}{\partial\mu}+\frac{\partial{L}}{\partial\sigma^2}\frac{\partial{\sigma^2}}{\partial{\mu}} ∂μ∂L=∂Znormi∂L∂μ∂Znormi+∂σ2∂L∂μ∂σ2 = ∂ L ∂ Z n o r m i − 1 σ 2 + ϵ + ∂ L ∂ σ 2 − 2 ∑ i = 1 m ( z i − μ ) m =\frac{\partial{L}}{\partial{Z_{norm}^i}}\frac{-1}{\sqrt{\sigma^2+\epsilon}}+\frac{\partial{L}}{\partial\sigma^2}\frac{-2\sum_{i=1}^{m}(z^i-\mu)}{m} =∂Znormi∂Lσ2+ϵ−1+∂σ2∂Lm−2∑i=1m(zi−μ)
∂ L ∂ Z i = ∂ L ∂ Z n o r m i ∂ Z n o r m i ∂ Z i + ∂ L ∂ σ 2 ∂ σ 2 ∂ Z i + ∂ L ∂ μ ∂ μ ∂ Z i \frac{\partial{L}}{\partial{Z^i}}=\frac{\partial{L}}{\partial{Z_{norm}^i}}\frac{\partial{Z_{norm}^i}}{\partial{Z^i}}+\frac{\partial{L}}{\partial\sigma^2}\frac{\partial{\sigma^2}}{\partial{Z^i}}+\frac{\partial{L}}{\partial\mu}\frac{\partial\mu}{\partial{Z^i}} ∂Zi∂L=∂Znormi∂L∂Zi∂Znormi+∂σ2∂L∂Zi∂σ2+∂μ∂L∂Zi∂μ = ∂ L ∂ Z n o r m i 1 σ 2 + ϵ + ∂ L ∂ σ 2 2 ( Z i − μ ) m + ∂ L ∂ μ 1 m =\frac{\partial{L}}{\partial{Z_{norm}^i}}\frac{1}{\sqrt{\sigma^2+\epsilon}}+\frac{\partial{L}}{\partial\sigma^2}\frac{2(Z^i-\mu)}{m}+\frac{\partial{L}}{\partial\mu}\frac{1}{m} =∂Znormi∂Lσ2+ϵ1+∂σ2∂Lm2(Zi−μ)+∂μ∂Lm1
-
测试
测试时一般每次只送入一个数据,计算其均值和方差都是有偏估计,但训练过程中保存了每一组batch每一层的均值和方差,则对每一层都可以使用均值和方差的无偏估计:
μ t e s t = E ( μ b a t c h ) σ t e s t 2 = m m − 1 E ( σ b a t c h 2 ) \mu_{test}=E(\mu_{batch})\\ \sigma^2_{test}=\frac{m}{m-1}E(\sigma^2_{batch}) μtest=E(μbatch)σtest2=m−1mE(σbatch2)
然后计算该层的输出:
Z ~ i = γ Z t e s t i − μ σ t e s t 2 + ϵ + β \widetilde{Z}^i=\gamma{\frac{Z^i_{test}-\mu}{\sqrt{\sigma_{test}^2+\epsilon}}}+\beta Z i=γσtest2+ϵZtesti−μ+β -
加在哪里
原始论文中加在激活函数前面,但改论文部分作者主张加在激活函数后面,从实践上来说也是加在激活函数后面效果更好。 -
局限
- 实验表明,当batch_size小于8时,BN反而会带来负面作用
- 不适用于RNN
详见:Batch Normalization原理与实战和Batch Normalization梯度反向传播推导
16.RNN和LSTM有什么不同?
RNN:
RNN(循环神经网络)最主要的特点就是每一步的输出不仅与这一步的输入有关,还跟上一步的输出有关。例如判断一句话中某个词是否是人名,不仅与这个词有关,还与这个词之前的那些单词有关。
其传播过程如下图所示:
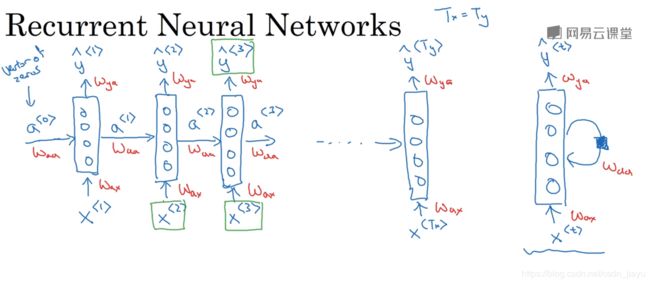
假设输入为x(长度为T),则输出公式如下:
a < t > = g ( W a a a < t − 1 > + W a x x < t > + b a ) a^{
y < t > = g ( W y a a < t > + b y ) y^{
其中 x < t > x^{
RNN的应用包括(1)many-to-many:上面讲的预测人名;或者语言翻译(2)many-to-one:情感预测(预测某部电影的情感)(3)one-to-many:音乐生成
RNN存在一个很大的问题就是梯度消失:当序列长度很长的时候(比如一个句子有100个单词),那么在反向传播的过程中,后面的梯度就很难对前面的参数产生影响,造成了梯度消失。
LSTM:
LSTM(长短时记忆)加入了“输入门”,“遗忘门”和“输出门”,解决了简单RNN序列太长梯度消失的问题。公式如下:
当 前 输 入 : z = t a n h ( W z [ a < t − 1 > , x t ] + b z ) 当前输入:z=tanh(W_z[a^{
输 入 门 : z i = s i g m o i d ( W i [ a < t − 1 > , x t ] + b i ) 输入门:z^i=sigmoid(W_i[a^{
遗 忘 门 : z f = s i g m o i d ( W f [ a < t − 1 > , x t ] + b f ) 遗忘门:z^f=sigmoid(W_f[a^{
输 出 门 : z o = s i g m o i d ( W o [ a < t − 1 > , x t ] + b o ) 输出门:z^o=sigmoid(W_o[a^{
更 新 c < t > : c < t > = z i ∗ z + z f ∗ c t − 1 更新c^{
更 新 a < t > : a < t > = z o ∗ t a n h ( c < t > ) 更新a^{
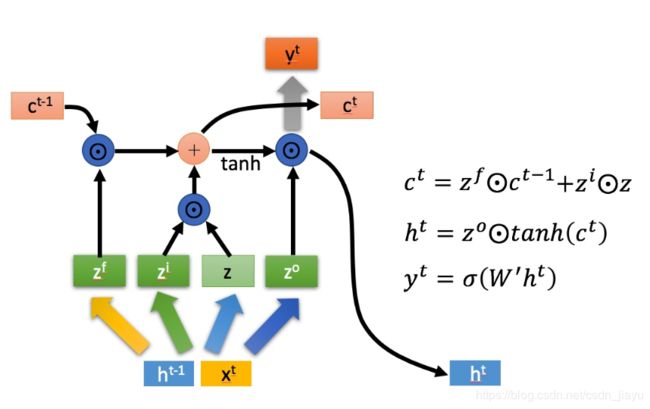
就这样,通过“门”的控制,LSTM遗忘不重要的信息,记住重要的信息,从而实现长期记忆。
详见:人人都能看懂的LSTM
17. 为什么RNN不用Relu函数而要用tanh函数?
CNN中用ReLU函数能解决梯度消失的问题是因为Relu函数梯度为1,能解决梯度爆炸的问题是因为反向传播时 W 1 , W 2 . . . W i W_1, W_2...W_i W1,W2...Wi互不相同,它们连乘很大程度上能抵消梯度爆炸的效果;而RNN中用Relu是若干个 W W W连乘,不能解决梯度爆炸的问题。所以想要解决RNN中的梯度消失问题,一般都是用LSTM。
详见:RNN中为什么要采用tanh而不是ReLu作为激活函数? - 何之源的回答 - 知乎
18.写一下卷积的实现
# coding=utf-8
import cv2 as cv
import numpy as np
def convolution(img, stride=1, pading='SAME'):
kernel=np.array([[1, 0, -1],
[1, 0, -1],
[1, 0, -1]]) # 卷积核
# 对原图进行填充
padding=int(kernel.shape[0]/2)
padding_fm=np.zeros((img.shape[0]+2*padding, img.shape[0]+2*padding))
padding_fm[padding:padding+img.shape[0], padding:padding+img.shape[1]]=img
result=np.zeros((int(img.shape[0]/stride), int(img.shape[1]/stride))) # 存放结果
# 卷积
for h_index in range(padding, padding_fm.shape[0]-padding, stride):
for w_index in range(padding, padding_fm.shape[1]-padding, stride):
roi=padding_fm[h_index-padding:h_index+padding+1,
w_index-padding:w_index+padding+1]
result[(int)((h_index-padding)/stride),
(int)((w_index-padding)/stride)]=np.sum(roi*kernel)
return result
if __name__=="__main__":
img=cv.imread('cat.jpg', 0)
cv.imshow('Origin image', img)
result = convolution(img, stride=2)
#print(result)
cv.imshow('After convolution', result)
19.空洞卷积的思想?或者说相比如标准卷积有什么改进?
- 标准卷积随着层数加深,虽然感受野会增大,但是分辨率会降低,这样不利于检测小目标;而空洞卷积可以在增大感受野的同时保持分辨率不变,有利于提升小目标的检测率,同时能对目标精确定位。
- 改变空洞卷积中的dilation rate,就能获得多尺度信息。
详见:总结-空洞卷积(Dilated/Atrous Convolution)
机器学习
1.介绍一下线性回归
对于给定数据集 ( X , Y ) = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x i , y i ) , . . . ( x m , y m ) (X, Y)={(x_1, y_1), (x_2, y_2), ...(x_i, y_i),...(x_m, y_m)} (X,Y)=(x1,y1),(x2,y2),...(xi,yi),...(xm,ym) ,其中 x i = ( x i 1 , x i 1 , . . . x i n ) x_i=(x_{i1}, x_{i1}, ...x_{in}) xi=(xi1,xi1,...xin),我们试图找到参数 W = ( w 1 , w 2 , . . . w n ) W=(w_1, w_2, ...w_n) W=(w1,w2,...wn)和 b b b使得 y i = W x i + b y_i=Wx_i+b yi=Wxi+b。为了找到这样的参数,我们定义损失函数:
L = − 1 2 m ∑ i = 1 m ( ( W x i + b ) − y i ) 2 L=-\frac{1}{2m}\sum_{i=1}^{m}((Wx_i+b)-y_i)^2 L=−2m1i=1∑m((Wxi+b)−yi)2
想让Loss最小化。所以我们用梯度下降法(梯度方向为什么是函数值下降最快方向在问题9已经证明):
∂ L ∂ W = − 1 m ( W x i + b − y i ) x i \frac{\partial{L}}{\partial{W}}=-\frac{1}{m} (Wx_i+b-y_i)x_i ∂W∂L=−m1(Wxi+b−yi)xi
∂ L ∂ b = − 1 m ( W x i + b − y i ) \frac{\partial{L}}{\partial{b}}=-\frac{1}{m} (Wx_i+b-y_i) ∂b∂L=−m1(Wxi+b−yi)
W和b的偏导都计算完之后利用如下公式更新W和b:
W = W − α ∂ L ∂ W W=W-\alpha \frac{\partial{L}}{\partial{W}} W=W−α∂W∂L
b = b − α ∂ L ∂ b b=b-\alpha \frac{\partial{L}}{\partial{b}} b=b−α∂b∂L
其中 α \alpha α表示学习率,一般取0.01~0.1.
除了梯度下降法,当 X T X X^T X XTX可逆的时候,还可以用正规方程法。此时的损失函数用矩阵形式表示(此处为方便表示,将参数b当做参数W的一部分):
L = − ( y − X W ) T ( y − X W ) L=-(y-XW)^T (y-XW) L=−(y−XW)T(y−XW)
根据公式 ∂ U T V ∂ x = ∂ U ∂ x V + ∂ V ∂ x U \frac{\partial{U^T V}}{\partial{x}}=\frac{\partial{U}}{\partial{x}}V + \frac{\partial{V}}{\partial{x}}U ∂x∂UTV=∂x∂UV+∂x∂VU有
∂ L ∂ W = − ∂ ( y − X W ) T ( y − X W ) ∂ W = − ∂ ( y − X W ) ∂ W ( y − X W ) − ∂ ( y − X W ) ∂ W ( y − X W ) = 2 X T ( y − X W ) \frac{\partial{L}}{\partial{W}}=-\frac{\partial{(y-XW)^T (y-XW)}} {\partial{W}}\\ =-\frac{\partial{(y-XW)}} {\partial{W}} (y-XW) - \frac{\partial{(y-XW)}} {\partial{W}}(y-XW)\\ =2X^T(y-XW) ∂W∂L=−∂W∂(y−XW)T(y−XW)=−∂W∂(y−XW)(y−XW)−∂W∂(y−XW)(y−XW)=2XT(y−XW)
令 ∂ L ∂ W = 0 \frac{\partial{L}}{\partial{W}}=0 ∂W∂L=0,可得 W = ( X T X ) − 1 X y W=(X^TX)^{-1}Xy W=(XTX)−1Xy
2.推导一下逻辑回归(LR)
注:一般来说LR指的是逻辑回归,而不是线性回归
线性回归得到的是一个数值,如果想要得到的 y ^ \hat y y^是类别,只需找一个单调可微的函数将线性回归的预测值与类别关联起来即可。而逻辑回归(准确来说应该是对数几率回归,叫逻辑回归是翻译问题)用的就是 s i g m o i d sigmoid sigmoid函数:
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
对线性回归 W x + b Wx+b Wx+b的值用 s i g m o i d sigmoid sigmoid函数即可得到类别:
y ^ = g ( W x + b ) = 1 1 + e − ( W x + b ) \hat y=g(Wx+b) =\frac{1}{1+e^{-(Wx+b)}} y^=g(Wx+b)=1+e−(Wx+b)1
其中 y ^ \hat y y^表示数据 x x x属于类别 y y y的概率,那么很明显, 1 − y ^ 1-\hat y 1−y^就表示数据 x x x不属于类别 y y y的概率。也即:
p ( y ^ = 1 ∣ x , W , b ) = 1 1 + e − ( W x + b ) = e W x + b 1 + e W x + b p(\hat y=1 | x, W, b) =\frac{1}{1+e^{-(Wx+b)}} =\frac{e^{Wx+b}} {1+e^{Wx+b}} p(y^=1∣x,W,b)=1+e−(Wx+b)1=1+eWx+beWx+b
p ( y ^ = 0 ∣ x , W , b ) = 1 − p ( y ^ = 1 ∣ x , W , b ) = 1 1 + e W x + b p(\hat y=0 | x, W, b) =1-p(\hat y=1 | x, W, b) =\frac{1} {1+e^{Wx+b}} p(y^=0∣x,W,b)=1−p(y^=1∣x,W,b)=1+eWx+b1
根据极大似然法,我们就是要找到一组参数 W , b W, b W,b使得 P ( Y ^ = Y ∣ W , b , X ) P(\hat Y=Y|W, b, X) P(Y^=Y∣W,b,X)最大:
P ( Y ^ = Y ∣ W , b , X ) = ∏ i = 1 m P ( y ^ i = y i ∣ x i , W , b ) P(\hat Y=Y|W, b, X) =\prod_{i=1}^{m} P(\hat y_i=y_i | x_i, W, b) P(Y^=Y∣W,b,X)=i=1∏mP(y^i=yi∣xi,W,b)
这样的连乘会造成数值下溢,所以取对数:
l n ∏ i = 1 m P ( y ^ i = y i ∣ x i , W , b ) = ∑ i = 1 m l n P ( y ^ i = y i ∣ x i , W , b ) = ∑ i = 1 m ( y i l n P ( y ^ i = 1 ∣ x i , W , b ) + ( 1 − y i ) l n P ( y ^ i = 0 ∣ x i , W , b ) ) = ∑ i = 1 m ( y i l n ( g ( W x i + b ) ) + ( 1 − y i ) l n ( 1 − g ( W x i + b ) ) ) ln \prod_{i=1}^{m} P(\hat y_i=y_i | x_i, W, b)\\ =\sum_{i=1}^{m} ln P(\hat y_i=y_i | x_i, W, b)\\ =\sum_{i=1}^{m} (y_i ln P(\hat y_i=1| x_i, W, b) + (1-y_i) ln P(\hat y_i=0| x_i, W, b))\\ =\sum_{i=1}^{m} (y_i ln (g(Wx_i+b)) + (1-y_i) ln (1-g(Wx_i+b))) lni=1∏mP(y^i=yi∣xi,W,b)=i=1∑mlnP(y^i=yi∣xi,W,b)=i=1∑m(yilnP(y^i=1∣xi,W,b)+(1−yi)lnP(y^i=0∣xi,W,b))=i=1∑m(yiln(g(Wxi+b))+(1−yi)ln(1−g(Wxi+b)))
找到 W , b W, b W,b使得 P ( Y ^ = Y ∣ W , b , X ) P(\hat Y=Y|W, b, X) P(Y^=Y∣W,b,X)最大,就是找到 W , b W, b W,b使得 − P ( Y ^ = Y ∣ W , b , X ) -P(\hat Y=Y|W, b, X) −P(Y^=Y∣W,b,X)最小。由此,我们定义损失函数:
L = − 1 m ∑ i = 1 m y i l n ( g ( W x i + b ) ) + ( 1 − y i ) l n ( 1 − g ( W x i + b ) ) L=-\frac{1}{m} \sum_{i=1}^{m} y_i ln (g(Wx_i+b)) + (1-y_i) ln (1-g(Wx_i+b)) L=−m1i=1∑myiln(g(Wxi+b))+(1−yi)ln(1−g(Wxi+b))
用梯度下降法最小化 L L L可得:
∂ L ∂ W = − 1 m ∑ i = 1 m ( y i h ( 1 − h ) h x i + ( 1 − y i ) − h ( 1 − h ) 1 − h x i ) = − 1 m ∑ i = 1 m ( y i − h ) x i \frac{\partial L}{\partial W} =-\frac{1}{m} \sum_{i=1}^{m} (y_i\frac{h(1-h)}{h}x_i + (1-y_i)\frac{-h(1-h)}{1-h}x_i)\\ =-\frac{1}{m} \sum_{i=1}^{m} (y_i-h)x_i ∂W∂L=−m1i=1∑m(yihh(1−h)xi+(1−yi)1−h−h(1−h)xi)=−m1i=1∑m(yi−h)xi
∂ L ∂ b = 1 m ∑ i = 1 m ( y i h ( 1 − h ) h + ( 1 − y i ) − h ( 1 − h ) 1 − h = − 1 m ∑ i = 1 m ( y i − h ) \frac{\partial L}{\partial b} =\frac{1}{m} \sum_{i=1}^{m} (y_i\frac{h(1-h)}{h} + (1-y_i)\frac{-h(1-h)}{1-h}\\ =-\frac{1}{m} \sum_{i=1}^{m} (y_i-h) ∂b∂L=m1i=1∑m(yihh(1−h)+(1−yi)1−h−h(1−h)=−m1i=1∑m(yi−h)
W = W − α ∂ L ∂ W = W − α m ( h − y i ) x i W=W-\alpha \frac{\partial L}{\partial W}=W-\frac{\alpha}{m} (h-y_i)x_i W=W−α∂W∂L=W−mα(h−yi)xi
b = b − α ∂ L ∂ b = b − α m ( h − y i ) b=b-\alpha \frac{\partial L}{\partial b}=b-\frac{\alpha}{m} (h-y_i) b=b−α∂b∂L=b−mα(h−yi)
3.偏差与方差
如果令 y y y表示数据的标记(label), f ( x ) f(x) f(x)表示测试数据的预测值, f ( x ) ‾ \overline{f(x)} f(x)表示学习算法对所有数据集的期望预测值。
则偏差表示期望预测值 f ( x ) ‾ \overline{f(x)} f(x)与标记 y y y之间的差距,差距越大说明偏差越大;而方差是测试预测值 f ( x ) f(x) f(x)与预测值的期望值 f ( x ) ‾ \overline{f(x)} f(x)之间的差距,差距越大说明方差越大。
也就是说,偏差表征模型对数据的拟合能力;而方差表征数据集的变动导致的学习性能的变化,也就是泛化能力。
详见博客:偏差与方差
4.介绍一下SVM
SVM要解决的问题和逻辑回归类似,就是要找到一个超平面将数据 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x i , y i ) , . . . ( x m , y m ) (x_1, y_1), (x_2, y_2), ... (x_i, y_i), ... (x_m, y_m) (x1,y1),(x2,y2),...(xi,yi),...(xm,ym)分开。只不过逻辑回归标定的类别是1和0,而SVM标定的类别是1和-1。也即找到一个超平面 W x + b Wx+b Wx+b使得 W x i + b > 0 Wx_i+b>0 Wxi+b>0时 y i = 1 y_i=1 yi=1, W x i + b < 0 Wx_i+b<0 Wxi+b<0时 y i = − 1 y_i=-1 yi=−1。
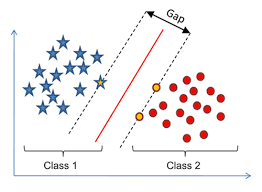
在空间中,这样的超平面有无数个,我们希望找到一个能将数据分得最“好”的超平面。而空间中任意样本点距离到超平面距离为: ∣ W x + b ∣ ∣ ∣ W ∣ ∣ \frac{|Wx+b|}{||W||} ∣∣W∣∣∣Wx+b∣
当 y i = 1 时 , W x i + b > 0 y_i = 1时,Wx_i + b > 0 yi=1时,Wxi+b>0,当 y i = − 1 时 , W x i + b < 0 y_i = -1时,Wx_i + b < 0 yi=−1时,Wxi+b<0
通过缩放变换使得下式成立:
{ W x i + b > = 1 y i = + 1 W x i + b < = − 1 y i = − 1 \begin{cases}Wx_i+b>=1 \quad y_i=+1 \\\\ Wx_i+b<=-1 \quad y_i=-1\end{cases} ⎩⎪⎨⎪⎧Wxi+b>=1yi=+1Wxi+b<=−1yi=−1
而离超平面最近的几个点使得上式中的等式成立,所以“最大间隔”(上图中的gap)等于 2 ∣ ∣ W ∣ ∣ \frac{2}{||W||} ∣∣W∣∣2,优化目标就是要使“最大间隔”最大化,等价于最小化 1 2 ∣ ∣ W ∣ ∣ 2 \frac{1}{2} ||W||^2 21∣∣W∣∣2,即:
m i n 1 2 ∣ ∣ W ∣ ∣ 2 s . t . y i ( W x i + b ) > = 1 i = 1 , 2 , . . . , m min\frac{1}{2} ||W||^2 \\ s.t. \quad y_i(Wx_i+b)>=1 \quad i=1, 2, ... , m min21∣∣W∣∣2s.t.yi(Wxi+b)>=1i=1,2,...,m
这个式子是个凸二次规划问题,能直接求解,但直接求解太麻烦,所以用拉格朗日乘子法计算它的对偶问题。
首先写出优化目标的拉格朗日函数:
L ( w , b , α ) = 1 2 ∣ ∣ W ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( W x i + b ) ) L(w, b, \alpha) = \frac{1}{2} ||W||^2 + \sum_{i=1}^{m} \alpha _i (1-y_i(Wx_i+b)) L(w,b,α)=21∣∣W∣∣2+i=1∑mαi(1−yi(Wxi+b))
其中 α i = ( α 1 , α 2 , . . . , α m ) \alpha _i=(\alpha _1, \alpha _2, ..., \alpha _m) αi=(α1,α2,...,αm)。对w和b求偏导,令偏导等于0可得:
W = ∑ i = 1 m α i y i x i W=\sum_{i=1}^{m} \alpha _i y_i x_i W=i=1∑mαiyixi
b = ∑ i = 1 m α i y i b=\sum_{i=1}^{m} \alpha _i y_i b=i=1∑mαiyi
将w和b带回拉格朗日函数得就成功得到优化目标的对偶函数:
L = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . α i y i = 0 , a i > = 0 , i = 1 , 2 , . . . , m L=\sum_{i=1}^{m} \alpha _i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha _i \alpha _j y_i y_j x_i^T x_j \\ s.t. \quad \alpha_i y_i=0, a_i>=0, i=1, 2, ..., m L=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t.αiyi=0,ai>=0,i=1,2,...,m
接下来用SMO算法求解 α \alpha α即可。SMO算法主要思想如下:
(1)选取一对需要更新的变量 α i 、 α j \alpha_i 、\alpha_j αi、αj(应使得选取样本所对应的样本之间的间隔最大)
(2)固定 α i 、 α j \alpha_i 、\alpha_j αi、αj以外的参数,求解损失函数L以更新 α i 、 α j \alpha_i 、\alpha_j αi、αj
(3)不断迭代(1)、(2)直到收敛
核函数
当数据线性不可分时,就需要将数据映射到高维空间进行分割。而只要数据的属性数量是有限的,那么一定可以找到一个高维特征空间使得数据线性可分。将数据映射到高维特征空间后,数据形式为 φ ( x ) \varphi(x) φ(x),此时对应的优化目标:
L = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j φ ( x i T ) φ ( x j ) s . t . α i y i = 0 , a i > = 0 , i = 1 , 2 , . . . , m L=\sum_{i=1}^{m} \alpha _i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha _i \alpha _j y_i y_j \varphi(x_i^T) \varphi(x_j) \\ s.t. \quad \alpha_i y_i=0, a_i>=0, i=1, 2, ..., m L=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjφ(xiT)φ(xj)s.t.αiyi=0,ai>=0,i=1,2,...,m
这样就要计算 φ ( x i ) 、 φ ( x j ) \varphi(x_i)、\varphi(x_j) φ(xi)、φ(xj)的内积,但高维特征空间的维数可能很高,甚至可能是无穷维,所以直接计算内积同时很困难,这个时候就需要找到一个函数k使得:
k ( x i , x j ) = < φ ( x i ) , φ ( x j ) > k(x_i, x_j)=<\varphi(x_i), \varphi(x_j)> k(xi,xj)=<φ(xi),φ(xj)>
对于一个对称函数,只要它的核矩阵半正定,那它就可以做核函数。常见的核函数有线性核、多项式核、高斯核、sigmoid核等。
软间隔与硬间隔的区别
硬间隔是希望所有样本都被正确划分,而软间隔允许某些样本划分不正确,软间隔对应损失函数为:
1 2 ∣ ∣ W ∣ ∣ 2 + C ∑ i = 1 m l 0 / 1 ( y i ( W x i + b ) − 1 ) \frac{1}{2}||W||^2 + C \sum_{i=1}^{m}l_{0/1}(y_i(Wx_i + b) - 1) 21∣∣W∣∣2+Ci=1∑ml0/1(yi(Wxi+b)−1)
C C C越大,越需要 ( y i ( W x i + b ) − 1 ) > = 0 (y_i(Wx_i + b) - 1)>=0 (yi(Wxi+b)−1)>=0,即希望所有样本分类正确,越接近硬间隔。
5.讲一讲PCA(SVD)
主成分分析(PCA)就是找到一个k维空间,将原数据投影到k维空间,使得投影距离最小的算法。其主要步骤如下:
(1)对数据各个维度进行归一化
(2)计算协方差矩阵 ∑ = 1 m ∑ i = 1 n X T X \sum=\frac{1}{m}\sum_{i=1}^{n} X^TX ∑=m1i=1∑nXTX
其中 X X X是特征缩放后的特征向量, ∑ ∈ R n ∗ n \sum\in{R}^{n*n} ∑∈Rn∗n。
(3)计算特征向量矩阵U(可用 [ U , S , D ] = s v d ( ∑ ) [U, S, D]=svd(\sum) [U,S,D]=svd(∑)计算,SVD的推导过程可以在相关的线性代数书籍上找到),得到 U = ( u ( 1 ) U ( 2 ) . . . U ( 3 ) ) U=\begin{pmatrix}u^{(1)}&U^{(2)}&...&U^{(3)}\end{pmatrix} U=(u(1)U(2)...U(3))
U ∈ R n ∗ n , U ( i ) ∈ R n ∗ n U\in{R}^{n*n}, U^{(i)}\in{R}^{n*n} U∈Rn∗n,U(i)∈Rn∗n。
(4)取前k列得 U r e d u c e = ( U ( 1 ) U ( 2 ) . . . U ( k ) ) U_{reduce}=\begin{pmatrix}U^{(1)}&U{(2)}&...&U{(k)}\end{pmatrix} Ureduce=(U(1)U(2)...U(k))
,最后得到降维后的数据 Z = X ⋅ U r e d u c e Z=X\cdot{U_{reduce}} Z=X⋅Ureduce, Z ∈ R m ∗ k Z\in{R}^{m*k} Z∈Rm∗k
其中k的取法为:
投影距离平方的平均: 1 m ∑ i = 1 m ∣ ∣ x i − x a p p r o x i ∣ ∣ 2 \frac{1}{m}\sum_{i=1}^{m}||x^i-x^i_{approx}||^2 m1∑i=1m∣∣xi−xapproxi∣∣2
数据原本的总变差: 1 m ∑ i = 1 m ∣ ∣ x i ∣ ∣ 2 \frac{1}{m}\sum_{i=1}^{m}||x^i||^2 m1∑i=1m∣∣xi∣∣2
取 1 m ∑ i = 1 n ∣ ∣ x i − x a p p r o x i ∣ ∣ 2 1 m ∑ i = 1 n ∣ ∣ x i ∣ ∣ 2 < 0.01 \frac{\frac{1}{m}\sum_{i=1}^{n}||x^i-x^i_{approx}||^2}{\frac{1}{m}\sum_{i=1}^{n}||x^i||^2}<0.01 m1∑i=1n∣∣xi∣∣2m1∑i=1n∣∣xi−xapproxi∣∣2<0.01时的k值。
Q:PCA为什么有效?
A:从信号的角度来看,大多数能量储存在低频信号。
6.数据不均衡怎么办?
数据不均衡(例如目标检测中正例很少,负例却很多)一般有4种办法:
- 欠采样:对负例进行欠采样。一种代表性算法是将负例分成很多份,每次用其中一份和正例一起训练,最后用集成学习综合结果。
- 过采样:对正例进行过采样。一种代表性方法是堆正例进行线性插值来获得更多的正例。
- 调整损失函数:训练时正常训练,分类时将数据不均衡问题加入到决策过程中。例如在我做的文本检测项目中,正常训练,但是判断某个像素是否是文本时 L o s s = − β Y l o g Y ^ − ( 1 − β ) ( 1 − Y ) l o g ( 1 − Y ^ ) Loss=-\beta{Y}log\hat{Y}-(1-\beta)(1-Y)log(1-\hat{Y}) Loss=−βYlogY^−(1−β)(1−Y)log(1−Y^)。其中 Y Y Y是样本的标记, Y ^ \hat{Y} Y^是预测值, β \beta β是负样本和总体样本的比值。通过加入 β \beta β和 1 − β 1-\beta 1−β使得数量较少的正样本得到更多的关注,不至于被大量的负样本掩盖。
- 组合/集成学习:例如正负样本比例1:100,则将负样本分成100份,正样本每次有放回采样至与负样本数相同,然后取100次结果进行平均。
7.有哪些经典的聚类算法?
1.原型聚类
所谓“原型”指的是样本空间中具有代表性的点。原型聚类的代表性算法是k-means算法:
- 随机选取k个点
- 依次计算剩下所有的点到这k个点的距离,并分分配给这k个点,形成k个簇
- 计算k簇点的均值,作为其新的中心点。重新计算所有的点这个k个中心点的距离,并将这些点重新分配给新计算出的中心点。
- 重复3,直到点属于的簇不再变化。
复杂度为O(n)。
2.密度聚类
- 随意选取一个点p
- 如果p点是核心对象(邻域eps范围内有超过MinPts个点),则寻找并合并p密度可达的点
- 如果p点不是核心对象,就重新选取一个点
- 重复1-3,直到所有的点被处理
3.层次聚类
层次聚类有自底向上和自顶向下两种聚合策略,这里以自底向上距离
- 所有的点每个点都属于一类
- 两两计算所有类的距离,将距离最近的两类合并为一类
- 计算新和成的类与其他所有点的距离,将距离最近的两类合并为一类
- 重复3,直到达到终止条件(如已经得到k个类)
详见博客:各种聚类算法的系统介绍和比较
8. 归一化的好处?哪些模型需要归一化?
归一化的好处主要有两点:
- 加快收敛速度:在进行梯度下降的过程中,如果不进行归一化,那下降过程很可能会是“之”字形,归一化后每一步都朝着损失函数最低点前进。
- 提升模型效果:如果不进行归一化,模型可能会偏向尺度较大的特征,导致模型交过变差。
AdaBoost、GBDT、XGBoost、LR、SVM之类的最优化算法需要归一化;而决策树、RF这类的概率模型主要关注变量的分布,是否缩放不影响分裂点,所以不需要归一化。
详见:机器学习中一些模型为什么要对数据归一化?
10. k-measn的k值如何确定?
- 经过数据分析得到数据的先验知识,从而确定k值。
- 用肘部法则,寻找代价值变化很大的点。
- 轮廓系数法:通过枚举不同的k值,计算不同k值下的平均轮廓系数,找到平均轮廓系数最大的k值。
详见:k-means的k值该如何确定?
11. KNN的k值选取方法的k值大小的影响?
先取一个较小值,然后通过交叉验证选取最优值。
k太小会导致过拟合,因为这样选的点数太少,在测试集上泛化性能不高;k太大会导致欠拟合,因为加入了很多无关点,导致模型你和能力差。
12. GBDT和XGBoost的区别?
- GBDT用CART作为基分类器,只能用于回归;XGBoost既能用于回归,又能用于分类。
- GBDT优化时只用到一阶导数信息;而XGBoost进行了泰勒展开,用到了二阶导数信息,加快了收敛速度,同时用泰勒展开取得函数做自变量的二阶导数形式,使得XGBoost只依靠数据就能选取分裂点,不依靠模型,这就是为什么XGBoost既能用于分类,又能用于回归。
- XGBoost在代价函数加入了正则项,降低了过拟合的可能性。
- GBDT只能串行;而XGBoost在训练之前,预先对数据的特征值进行了排序,保存为block结构,使得XGBoost支持特征粒度的并行。
- GBDT没有对缺失值进行处理,而XGBoost对缺失值做了处理(和lightgbm一样,每次分割的时候,分别把缺失值放在左右两边各计算一次,然后比较两种情况的增益,择优录取。)。
- GBDT每次用所有的特征进行分裂,XGBoost类似随机森林每次随机选择一部分特征进行分裂。
详见:RF、GBDT、XGBoost常见面试题整理
13.XGboost的损失函数?XGBoost哪些参数可以用来防止过拟合?
L t = ∑ i = 1 m l ( F t − 1 ( x i ) + f t ( x i ) , y i ) + 1 2 λ ∑ i = 1 t W j 2 = ∑ i = 1 m l ( F t − 1 x i , y i ) + l ′ ( F t − 1 x i , y i ) f t ( x i ) + 1 2 l ′ ′ ( F t − 1 x i , y i ) f t 2 ( x i ) + 1 2 λ ∑ i = 1 t W j 2 L_t = \sum_{i=1}^{m}l(F_{t-1}(x_i)+f_t(x_i), y_i)+\frac{1}{2}\lambda \sum_{i=1}^{t}W_j^2 \\=\sum_{i=1}^{m}l(F_{t-1}x_i, y_i)+l^{'}(F_{t-1}x_i, y_i)f_t(x_i)+\frac{1}{2}l^{''}(F_{t-1}x_i, y_i)f_t^2(x_i)+\frac{1}{2}\lambda \sum_{i=1}^{t}W_j^2 Lt=i=1∑ml(Ft−1(xi)+ft(xi),yi)+21λi=1∑tWj2=i=1∑ml(Ft−1xi,yi)+l′(Ft−1xi,yi)ft(xi)+21l′′(Ft−1xi,yi)ft2(xi)+21λi=1∑tWj2
其中 G j G_j Gj和 H j H_j Hj分别是 l ( F t − 1 ( x ) , y ) l(F_{t-1}(x), y) l(Ft−1(x),y)的一阶和二阶展开式。
可以用l1、l2、数的深度max_depth、属性采样率subsample_bytree和样本采样率subsample。
14.XGBoost和LightGBM的区别?
- XGBoost是level-wise的,不论结点分裂的增益大小都进行分裂;而LightGBM是leaf-wise的,只对当前增益最大的结点进行分裂。所以LightGBM更高效,但也更容易过拟合,所以要控制叶子数。
- LightGBM采用Histogram算法,只用存储特征离散化后的值,降低了存储开销;而且XGBoost需要对每个特征值都进行分裂计算增益,而LightGBM只进行k次分裂。
- LightGBM进行了直方图加速:一个叶子结点的直方图可以由它的父亲直方图减去兄弟直方图得到。
15.特征选择方法有哪些?
(1)过滤式选择:比如利用Pearson系数进行特征选择。
(2)包裹式选择:每次随机选择一部分特征进行交叉验证,如果loss能降低或者loss相同但维数更少,就更新特征子集。最终留下来的特征子集就是需要的特征。
(3)嵌入式选择:把特征选择过程和模型学习过程融为一体,也就是L1和L2正则化。
(4)用xgboots、lightgbm或Random Forest自带的特征重要程度排序进行选择。
16.XGBoost和Random Forest单棵树谁的深度更深?
XGBoost是boosting算法,boosting算法是根据每一轮的表现调整训练数据的权重,所以关注的是降低偏差;而对一个算法来说,要同时关注偏差和方差,所以boosting算法的基学习器必须要方差小。Random Forest是bagging算法,对数据自主采样后各自训练,通过加权各棵树来降低方差;其基学习器和单棵决策树训练一样,主要在关注降低偏差。
详见:为什么xgboost/gbdt在调参时为什么树的深度很少就能达到很高的精度? - 于菲的回答 - 知乎
图像处理
1.图像处理的知识
-
有哪些常用滤波器?
GaussianBlur
MediumBlur
MeanBlur -
边缘检测算子有哪些?
canny算子(一阶差分)
sobel算子(一阶差分)
laplacian算子(二阶差分)
(先进行滤波,再进行边缘检测)
- canny算子是怎么做的?
(1)将图像处理成灰度图
(2)进行高斯滤波
(3)分别计算x方向和y方向梯度,再用平方和开根号计算综合梯度
(4)用非极大值抑制去除非边缘像素
(5)设置高阈值和低阈值:大于高阈值的被保留;低于低阈值的被抛弃;处于低阈值和高阈值之间的,如果和高阈值像素相连则被保留,否则被放弃。
对比:canny算子检测的边缘很细,可能只有一个像素大小,没有强弱;sobel算子检测的边缘有强弱;laplacian算子对边缘很敏感,但可能会将不是边缘的也当成边缘。
详见:数字图像 - 边缘检测原理 - Sobel, Laplace, Canny算子
-
霍夫变换是干嘛的?
主要是用来提取直线特征的。(首先要进行边缘检测得到二值化图像,再进行霍夫变换) -
形态学操作
腐蚀(用周围的最大值填充)、膨胀(用周围的最小值填充):分别相当于“腐蚀”(减小)白色区域和“膨胀”(增大)白色区域。
开运算:先腐蚀后膨胀,把黑色区域连横一块。
闭运算:先膨胀后腐蚀,把黑色区域分成多块。
顶帽:原图与开运算之差。
黑帽:原图与闭运算之差。 -
漫水填充
将一块连通区域填充为某种指定颜色。一般用于获取掩码或者某块区域用。 -
图像直方图
直方图是一种数据统计的集合,统计数据可以是亮度、灰度、梯度任何能描述图像的特征。横轴表示强度值,纵轴表示该强度值区域下统计数据的数量。 -
mat申请矩阵后怎么释放内存?
mat.release()函数 -
RGB图像怎么转为灰度图?
opencv的cvtColor(src, COLOR_RGB2GRAY)函数,具体的算法是 g r a y = 0.299 ∗ R + 0.587 ∗ G + 0.114 ∗ B gray = 0.299*R + 0.587*G + 0.114*B gray=0.299∗R+0.587∗G+0.114∗B
2.传统的特征提取方法有哪些?
SIFT
- 构建DOG尺度空间:对原图进行多次采样,形成图像金字塔,这样做的目的是对于尺寸较大的图片获得概貌特征,对于尺寸较小的图片获得细节特征。对金字塔每一层的图片都用不同 σ \sigma σ值进行高斯滤波,由此每一层金字塔都有若干张图片,每一层金字塔称为一个尺度。
- 关键点定位:对于一个点是不是关键点,要用它和同尺度空间(包括不同 σ \sigma σ值)26个相邻点进行比较,如果这个点是最小点或最大点,那这个点就是关键点。得到关键点后进行曲线拟合,得到精确的关键点位置。
- 方向赋值:利用梯度直方图根据检测到的关键点的局部图像结构为特征点赋值。
- 生成描述子:描述子不但包括关键点,还包括周围对其有贡献的像素点,使关键点具有更多的不变特性,提高目标匹配效率。通过采样、坐标旋转和计算梯度直方图,最终形成n维SIFT特征向量。
HOG
- 图像灰度化
- 图像归一化(调节图像对比度,减小光照、阴影、噪声的影响)
- 计算每个像素的梯度
- 将图像分成一个个cells(如6*6/cell),统计每个小块内梯度直方图,就是每个cell的descriptor
- 将一个个cell合并成block,将一个block中各个cell的descriptor串联起来,就是每个block的HOG特征的descriptor。
- 将图形中所有block的HOG特征串联起来就是整幅图的HOG特征描述子。
SIFT提取的是关键点,而HOG提取的是边缘特征。CNN其实还在学习一个能很好地提取信息的滤波器。
SURF是对SIFT的改进,简化了其中一些运算,基本保留了SIFT的效果;ORB也是对SIFT的改进,基本上实现了实时性。
详见:图像处理之特征提取
3.两个图像库,场景一一对应,一个有雨滴,一个没有雨滴,对有雨滴的图像去除雨滴,要不留痕迹。
用opencv对两幅图进行模板匹配(templateMatch),然后圈出不同区域,用无雨滴的图块覆盖有雨滴的图块即可。
数据结构/算法
1.会写红黑树吗?
红黑树是一种常见的平衡二叉搜索树,它的查找、插入、删除操作时间复杂度都是O(log(n)),并且一直保持在log(n),不会像二叉搜索树那样,当数字有序的时候退化成一条链,时间复杂度编程O(n)。而它之所以保持这样的性质,是因为它的五条性质:
- 每个结点要么是红的,要么是黑的
- 根结点是黑的
- 叶节点(这里的叶结点和我们平时理解的叶结点不太一样,指的是叶结点下的NULL结点)都是黑的
- 如果一个结点是红色的,那么它的两个子结点都是黑的
- 对于任意一个结点,到它所有叶结点的每一条路径上黑色结点数量都一样
- 证明具有n个结点的红黑树最大高度是 2 l o g ( n + 1 ) 2log(n+1) 2log(n+1)
- 原命题为 h < = 2 l o g ( n + 1 ) h<=2log(n+1) h<=2log(n+1);要证 h < = 2 l o g ( n + 1 ) h<=2log(n+1) h<=2log(n+1),就是要证 l o g ( n + 1 ) > = h / 2 log(n+1)>=h/2 log(n+1)>=h/2;要证 l o g ( n + 1 ) > = h / 2 log(n+1)>=h/2 log(n+1)>=h/2,就是要证 n > = 2 h / 2 − 1 n>=2^{h/2}-1 n>=2h/2−1。
x的左右子树的高度不同,但根据性质5,x任意一条路径的黑色节点数相同。定义某一结点x到叶结点(不包括x)的任意一条路径上黑色结点的个数为黑高度,用 b h ( x ) bh(x) bh(x)来表示。
根据性质4, b h ( x ) > = h / 2 bh(x)>=h/2 bh(x)>=h/2,那么要证 n > = 2 h / 2 − 1 n>=2^{h/2}-1 n>=2h/2−1,只需证明 n > = 2 b h ( x ) − 1 n>=2^{bh(x)}-1 n>=2bh(x)−1即可。
利用归纳法来证明 n > = 2 b h ( x ) − 1 n>=2^{bh(x)}-1 n>=2bh(x)−1:
(1)当x的高度等于0时,x为空结点, 2 b h ( x ) − 1 = 2 0 − 1 = 0 2^{bh(x)}-1=2^{0}-1=0 2bh(x)−1=20−1=0成立
(2)当x的高度大于0时且有两个子树时:若子结点为红结点,则子结点的黑高度为 b h ( x ) bh(x) bh(x);若子结点为黑结点,则子结点的黑高度为 b h ( x ) − 1 bh(x)-1 bh(x)−1。如果子结点的结点数至少为 2 b h ( x ) − 1 − 1 2^{bh(x)-1}-1 2bh(x)−1−1成立,那么x结点的结点数至少为 2 b h ( x ) − 1 − 1 + 2 b h ( x ) − 1 − 1 + 1 = 2 b h ( x ) − 1 2^{bh(x)-1}-1+2^{bh(x)-1}-1+1=2^{bh(x)}-1 2bh(x)−1−1+2bh(x)−1−1+1=2bh(x)−1。即 n > = 2 b h ( x ) − 1 n>=2^{bh(x)}-1 n>=2bh(x)−1,所以原命题得证。
STL中的map和set都是用红黑树实现的。
了解以上知识即可,一般不需要实现红黑树。
2.复习一下排序算法。
冒泡排序
void bubbleSort(vector& nums)
{
for (int p = nums.size() - 1; p >= 0; p--) // 注意p不要导致nums[i]下标越界即可
{
bool hasChanged = false;
for (int i = 0; i < p; ++i)
{
if (nums[i] > nums[i + 1])
{
swap(nums[i], nums[i + 1]);
hasChanged = true;
}
}
if (hasChanged == false) // 如果某次排序过程一次交换也没有发生,说明数组已经有序
break;
}
}
插入排序
void insertSort(vector& nums)
{
for (int p = 1; p < nums.size(); ++p) // 从第一张牌开始摸(第0张牌不用摸),插入正确的位置
{
int temp = nums[p];
int i;
for (i = p; i > 0 && nums[i - 1] > temp; --i) // 牌的前面有更大的值
{
nums[i] = nums[i - 1]; // 腾出空位
}
nums[i] = temp; // 将牌放到正确的位置(注意这里是i不是i-1)
}
}
选择排序
void selectSort(vector& nums)
{
for (int p = 0; p < nums.size(); ++p)
{
int minIndex = p;
for (int i = p; i < nums.size(); ++i)
{
if (nums[i] < nums[minIndex]) // 比较的时候注意不要写错了
{
minIndex = i;
}
}
swap(nums[p], nums[minIndex]);
}
}
希尔排序
void shellSort(vector& nums) // 希尔排序是插入排序的进阶
{
for (int D = nums.size() / 2; D > 0; D /= 2) // 希尔排序增量
{
for (int p = D; p < nums.size(); p++) // 这里是p++
{
int temp = nums[p];
int i;
for (i = p; i >=D && nums[i - D] > temp; i -= D) // 注意这里是i>=D
{
nums[i] = nums[i - D];
}
nums[i] = temp;
}
}
}
归并排序
void mergeArray(vector& nums, vector& tempNums, int lstart, int rstart, int rend) // 合并两个相邻的有序子序列
{
int lend = rstart - 1;
int numSubArray = rend - lstart + 1;
int temp = lstart; // 存放结果数组的初始位置
while (lstart <= lend && rstart <= rend) // 直到左右指针相遇才能用完较小序列的所有元素
{
if (nums[lstart] <= nums[rstart]) // 这里比较的时候不要把nums忘了
{
tempNums[temp++] = nums[lstart++];
}
else
{
tempNums[temp++] = nums[rstart++];
}
}
while (lstart <= lend) // 直接复制左边剩下的
tempNums[temp++] = nums[lstart++];
while (rstart <= rend) // 直接复制右边剩下的
tempNums[temp++] = nums[rstart++];
// 将有序子列复制回原数组
for (int i = rend; i >= rend - numSubArray + 1; --i)
nums[i] = tempNums[i];
}
void mSort(vector& nums, vector& tempNums, int lstart, int rend)
{
if (lstart < rend) // 当子列只有一个数值,说明已经是有序的了
{
int center = (lstart + rend) / 2;
mSort(nums, tempNums, lstart, center); // 归并排序做子列
mSort(nums, tempNums, center + 1, rend); // 归并排序右子列
mergeArray(nums, tempNums, lstart, center+1, rend); // 主要这里是center+1
}
}
void mergeSort(vector& nums)
{
vector tempNums(nums);
mSort(nums, tempNums, 0, nums.size() - 1);
}
堆排序
void downAdjust(vector& nums, int low, int high)
{
int i = low, j = 2 * i + 1; // i是待调整结点,j是它的左节点
while (j <= high) // 存在孩子结点
{
// 找到子结点中更大的值
if (j + 1 <= high && nums[j + 1] > nums[j]) // 如果i的右结点存在且右节点更大
{
j = j + 1;
}
if (nums[i] < nums[j])
{
swap(nums[i], nums[j]);
i = j; // i变更为待调整结点
j = 2 * i + 1;
}
else // 无需再调整,说明下面已经是堆了
{
break;
}
}
}
void heapSort(vector& nums)
{
// 建大顶堆
for (int i = nums.size()/ 2-1; i >= 0; --i) // 从最后一个有子结点的结点开始调整,**直到第0个结点**
{
downAdjust(nums, i, nums.size() - 1); // 最后一个结点是nums.size() - 1
}
// 排序
for (int i = nums.size() - 1; i > 0; --i)
{
swap(nums[0], nums[i]); // 交换第一个和最后一个无序的数字
downAdjust(nums, 0, i - 1); // 要调整的是0到i-1
}
}
快速排序
void qSort(vector& nums, int left, int right)
{
if (left < right) // 当子序列只有一个数字时已经有序,无需再排序,只有子序列数字量大于1才排序
{
int begin = left, end = right; // 存储子序列的首尾位置
int pos = round(1.0*rand() / RAND_MAX * (right - left)) + left;
swap(nums[pos], nums[left]);
int temp = nums[left]; // 选取left处的值作为主元,用一个临时变量存储
while (left < right) // 直至左右指针相遇
{
while (lefttemp)
right--; // 只要右指针的值比主元大,就移动右指针
nums[left] = nums[right];
while (left < right && nums[left] <= temp) // 两次判断时至少有一次带=符号,否则会无限循环
left++; // 只要左指针的值比主元小,就移动左指针
nums[right] = nums[left];
}
nums[left] = temp; // 将主元放到正确的位置
qSort(nums, begin, left - 1);
qSort(nums, left + 1, end);
}
}
void quickSort(vector& nums)
{
srand((unsigned)time(NULL));
qSort(nums, 0, nums.size() - 1); // 注意这里的右边界是nums.size()-1
}
算法比较:
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 稳定 | O ( 1 ) O(1) O(1) | n小时较好 |
| 交换 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( 1 ) O(1) O(1) | n小时较好 |
| 选择 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定(例如:5 5 2) | O ( 1 ) O(1) O(1) | n小时较好 |
| 插入 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n2) O(n2) | 稳定 | O ( 1 ) O(1) O(1) | 大部分已排序时较好 |
| 基数 | O ( l o g R B ) O(logRB) O(logRB) | O ( l o g R B ) O(logRB) O(logRB) | 稳定 | O ( n ) O(n) O(n) | B是真数(0-9) R是基数(个十百) |
| Shell | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n s ) 1 < s < 2 O(n^s) \quad 1 |
不稳定 | O ( 1 ) O(1) O(1) | s是所选分组 |
| 快速 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( n l o g n ) O(nlogn) O(nlogn)(递归调用栈) | n大时较好 |
| 归并 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | 稳定 | O ( 1 ) O(1) O(1)(可以做到原地排序,不需要辅助空间;可以不用递归,而是自下而上归并) | n大时较好 |
| 堆 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | 不稳定 | O ( 1 ) O(1) O(1) | n大时较好 |
3.散列表解决冲突的方法有哪些?
- 线性探查法
遇到冲突时,将位置+1,直到没有冲突为止,这样做的缺点是容易扎堆。 - 平方探查法
遇到冲突时 + − i 2 +-i^2 +−i2.如果超出tablesize就对tablesize取余,小于0就加上tablesize。 - 链地址法
将散列值相同的键放在同一个单链表中,遇到冲突时就遍历单链表。 - 再哈希法
构造多个不同的散列函数。遇到冲突后,用新的散列函数取计算,直到不产生冲突为止。
详见:数据结构-浙江大学p123-p134
4.二叉树的递归遍历和非递归遍历
#include
#include
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}
};
void insertNode(TreeNode*& root, int x)
{
// 递归边界,插入节点
if (root == nullptr)
{
root = new TreeNode(x);
return;
}
if (x == root->val) // 刚好相等,说明结点已在树中
return; // 什么都不做
else if (x < root->val) // 递归往左插入
insertNode(root->left, x);
else // 递归往右插入
insertNode(root->right, x);
}
TreeNode* createBST(vector nums)
{
TreeNode* root = nullptr;
for (int i = 0; i < nums.size(); ++i) // 遍历每一个元素,依次加入树中
{
insertNode(root, nums[i]);
}
return root;
}
void preOrderRecursive(TreeNode* root)
{
if (root == nullptr)
return;
cout << root->val << " ";
preOrderRecursive(root->left);
preOrderRecursive(root->right);
}
void preOrderNoRecursive(TreeNode* root)
{
stack s;
TreeNode* cur = root;
while (!s.empty() || cur != nullptr) // 左子树没遍历完或右子树没遍历完
{
while (cur != nullptr) // 左子树没遍历完,一直遍历左边,遍历过程中输出根节点的值
{
cout << cur->val << " ";
s.push(cur);
cur = cur->left;
}
if (!s.empty())
{
cur = s.top();
s.pop();
cur = cur->right;
}
}
}
// BST的中序遍历相当于排序输出
void inOrderRecursive(TreeNode* root)
{
if (root == nullptr)
return;
inOrderRecursive(root->left);
cout << root->val << " ";
inOrderRecursive(root->right);
}
void inOrderNoRecursive(TreeNode* root)
{
stack s;
TreeNode* cur = root;
while (cur != nullptr || !s.empty())
{
while (cur != nullptr)
{
s.push(cur);
cur = cur->left;
}
if (!s.empty())
{
cur = s.top();
s.pop();
cout << cur->val << " ";
cur = cur->right;
}
}
}
void postOrderRecursive(TreeNode* root)
{
if (root == nullptr)
return;
postOrderRecursive(root->left);
postOrderRecursive(root->right);
cout << root->val << " ";
}
// 首先将根节点入栈,然后判断根节点是否有左右孩子,没有就直接访问
// 如果有左孩子或右孩子,但左右孩子都被访问过了,也能访问这个根节点
// 否则就先将右孩子入栈,再将左孩子入栈。这样访问顺序依次是左->右->根
void postOrderNoRecursive(TreeNode* root)
{
stack s;
TreeNode* cur = root; // 当前节点
TreeNode* pre = nullptr; // 前一次访问的节点
s.push(cur);
while (!s.empty())
{
cur = s.top(); // 此时不要将s.top()出栈,因为还没有决定是否要访问这个节点
if (cur->left == nullptr && cur->right == nullptr)
{
cout << cur->val << " ";
s.pop(); // 将访问了的节点出栈
pre = cur; // 设置访问节点为这个被访问的节点
}
// 如果不判断pre!=nullptr,可能cur刚好有一个孩子为空,但其实它的孩子没有被访问过
else if ((pre == cur->left || pre == cur->right) && pre != nullptr)
{
cout << cur->val << " ";
s.pop();
pre = cur;
}
else
{
if (cur->right != nullptr)
s.push(cur->right);
if (cur->left != nullptr)
s.push(cur->left);
}
}
}
int main()
{
// 建树(建立一颗二叉搜索树,这样中序遍历是排序数组,从而检验建树是否正确)
vector nums{ 4, 8, 3, 6, 5, 2 };
TreeNode* root = createBST(nums);
cout << "先序遍历(递归:) ";
preOrderRecursive(root);
cout << endl;
cout << "先序遍历(非递归:) ";
preOrderNoRecursive(root);
cout << endl;
cout << "中序遍历(递归:) ";
inOrderRecursive(root);
cout << endl;
cout << "中序遍历(非递归:) ";
inOrderNoRecursive(root);
cout << endl;
cout << "后序遍历(递归:) ";
postOrderRecursive(root);
cout << endl;
cout << "后序遍历(非递归:) ";
postOrderNoRecursive(root);
cout << endl;
system("pause");
return 0;
}
5.KMP算法
#include
#include
using namespace std;
vector getNext(char str[], int len)
{
vector next(len, -1); // 定义并初始化next数组
next[0] = -1;
int j = -1; // 初始化j = next[0] = -1
for (int i = 1; i < len; ++i)
{
while (j != -1 && str[i] != str[j + 1])
{
j = next[j];
}
if (str[i] == str[j + 1])
{
j++;
}
next[i] = j;
}
return next;
}
bool KMP(char* text, char* pattern)
{
int n = strlen(text), m = strlen(pattern); // 字符串的长度
if (n < m)
return false;
vector next = getNext(pattern, m); // 获取模式串的next数组
int j = -1; // i表示text中当前欲匹配字符,j表示pattern中已经匹配成功的字符,所以初始位置为-1
for (int i = 0; i < n; ++i)
{
while (j != -1 && text[i] != pattern[j + 1]) // 当前字符不匹配
{
j = next[j];
}
if (text[i] == pattern[j + 1])
{
j++; // 当前字符匹配,那么j需要增加1,i在下一轮的时候会增加1
}
if (j == m - 1)
return true; // pattern[m-1]匹配成功,说明pattern是text的子串
}
return false;
}
int main()
{
char text[] = "abababab", pattern[] = "abab";
bool isSubStr = KMP(text, pattern);
system("pause");
return 0;
}
操作系统/计算机网络/数据库
1.进程和线程的区别?
进程是程序的一次动态执行过程,一个程序可以包含多个进程(例如Chrome浏览器,每一个网页都是一个进程);线程是进程的一条执行流程,一个进程可以包含多个线程(例如计算天气预报的时候,就需要用多线程模式,多个线程之间并发运行)。
一个进程包含数据段、代码段、栈空间、堆空间以及该进程管理的资源,每个进程的地址空间都是独立的;而一个进程的多个线程之间共享数据段、代码段、堆空间和文件资源,每个线程有自己独立的栈空间,存放其局部变量、函数参数和返回值。

举个例子,你写了一个音乐播放器程序,这个程序内部实现分为读取数据、解码、送入声卡三块功能,想让这三块功能同时执行,就可以让这三款功能分为三个线程同时执行,而音乐播放器则是一个进程。
明白了这些之后,进程和线程的区别包括:
- 线程的创建和终止时间都比进程短,因为线程只需要考虑栈空间的创建和回收,不需要管理资源等。
- 切换同一个进程的不同线换比切换进程快,因为同一个进程的不同线程都在同一块地址空间,拥有同一个页表,不需要切换页表。
- 同一进程的不同线程共享内存和地址空间,可以进行不通过内核的通信。
- 多线程的优点是运行速度快,可以并发执行,但如果一个线程崩溃,所有的进程都会崩溃;多线程一个线程崩溃,其他线程不会受到影响,例如浏览网页一个网页崩溃了,其他网页不受影响。
详见:操作系统_清华大学(向勇、陈渝) p35-p44
2.什么是死锁?产生的原因?必要条件?解决办法?
- 定义:死锁是指多个进程之间循环等待彼此占有的资源而导致的无限僵持等待的局面。
- 产生的原因:第一是系统提供的资源太少,第二是程序设计不合理
- 必要条件:(1)某个资源一段时间内只能被一个进程占有,不能同时被两个及以上进程占有 (2)进程获得的资源在使用完之前,不能由进程申请者强行从资源占有者手中剥夺资源(3)进程占有资源后,又申请了一个新的被其他进程占有的资源,从而处在等待状态(4)若干个进程形成环,每个进程都占有对方申请的下一个资源
- 解决办法:典型的有鸵鸟算法(什么都不干)和银行家算法(每次申请新的资源之前判断能否申请这个资源)。
详见:死锁的原因,条件和解决办法
3.进程间的通信?
- 管道(pipe):是一种半双工通信,数据只能单向流动;且只能在具有亲缘关系的进程间使用。
- 命名管道(named_pipe):克服了管道没有名字的限制,因此能在不具有亲缘关系的进程间使用。
- 信号量(semaphore):信号量是一个计数器,用来控制多个进程对共享资源的访问。常作为一种锁机制,防止某个进程正在访问该资源时,其他进程也访问该资源。
- 信号(signal):信号是一种比较复杂的通信机制,用于接收通知进程某个事件已发生。
详见:Linux进程间通信的几种方式总结–linux内核剖析(七)
4.线程间的通信方式?
(1)通过全局变量进行通信,因为各个线程都能更改全局变量。
(2)通过消息进行通信,每个线程拥有自己的消息队列,因此可以通过消息进行线程通信。
(3)通过共享的内存和地址空间可以进行不经内核的通信。
详见:线程间的通信、同步方式与进程间通信方式
5.TCP传输为什么可靠(TCP是怎么实现可靠传输的)?
TCP实现可靠传输主要靠停止等待协议和自动重传请求,停止等待协议就是说每发送一个数据包就要求接收方发送确认信息,自动重传请求是如果超过RTT((往返)传播时延+(排队)等待时延+(应用程序)数据处理时延)时间还没收到确认信息,那就自动重传。TCP传输有以下四种情况:
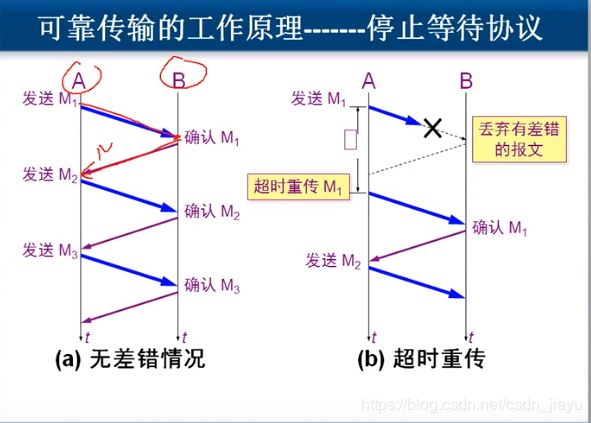

但是这样效率太低,所以采用累积确认的方法,即接收端收到若干条数据包才确认一次。如果发送方发出123456,接收方收到123(456还在传输路程中),那么接收方返回的确认好就是4(要求发送方发送4);如果发送方发出123456,但接收方收到的是124(56还在传输路程中),那么接收方返回的确认号就是3,发送方会重新发送3456。
而在事实上的网络中,TCP传输是以字节流发送数据的,因此采用滑动窗口来实现上述内容。在TCP建立连接的过程中,接收方会告诉发送方接收缓存以及接收窗口大小,那么发送方就将自己的发送窗口大小设置为接收窗口大小,将发送缓存设置为接收缓存大小。发送方先将数据包都扔到发送缓存中,然后在发送窗口中每次发送若干个字节(一直不停地发,不管是否收到确认,直到发送窗口中的字节发完),接收方累积收到若干字节后返回确认,发送方的发送窗口就可以在发送缓存中右移。如果字节丢失,接收方会告诉发送方丢失的是哪些字节,发送方只需重新发送那些字节即可,不需要像之前说的累积确认那样,再次发送丢失数据以及之后的所有数据。此时的超时重传采用加权平均法,加权平均往返时间 R T T n e w = ( 1 − α ) R T T o l d + α ∗ R T T n e w , α = 1 8 RTT_{new}=(1-\alpha)RTT_{old}+\alpha*RTT_{new}, \alpha=\frac{1}{8} RTTnew=(1−α)RTTold+α∗RTTnew,α=81,超时重传时间应略大于这个时间。
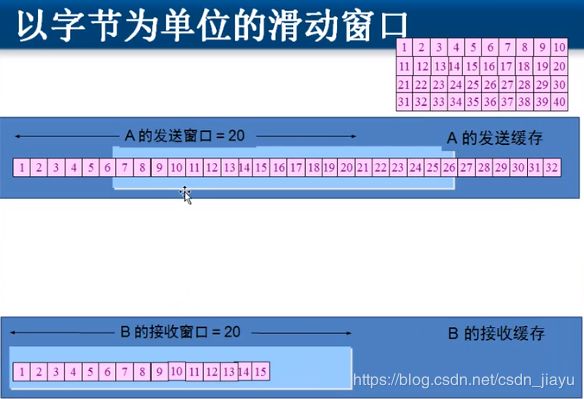
除此之外,TCP可靠传输还包括流量控制和拥塞控制。流量控制是在发送过程中,如果接收方应用程序来不及处理接收缓存中的字节,那么接收窗口大小就动态调整,发送窗口也相应地动态调整,从而实现了流量控制。拥塞控制是网络吞吐量随着负荷的增大而下降,所以发送窗口大小从1开始,指数增长,直至增大到超过一个阈值就加法增长,如果出现超时,就将阈值设为出现超时时发送窗口大小的一半,同时将发送窗口再次设为1,重复上述步骤。
详见:[面试时]我是如何讲清楚TCP/IP是如何实现可靠传输的
6. 拥塞控制
拥塞控制是防止过多的数据注入网络中,使网络中的路由器或链路不致过载。
拥塞控制方法包括慢开始、拥塞避免、快重传和快回复。
- 慢开始和拥塞避免:先用慢开始算法,也就是把拥塞窗口大小首先设置为1, 之后每经过一个轮次窗口大小增大两倍;当窗口大小超过慢开始门限值后就是用拥塞避免算法,也就是每次把窗口大小增加1。当出现超时重传时,就判断网络出现了拥塞,把慢开始门限值设置为出现拥塞时窗口大小的一半,然后重新使用慢开始算法和拥塞避免算法。
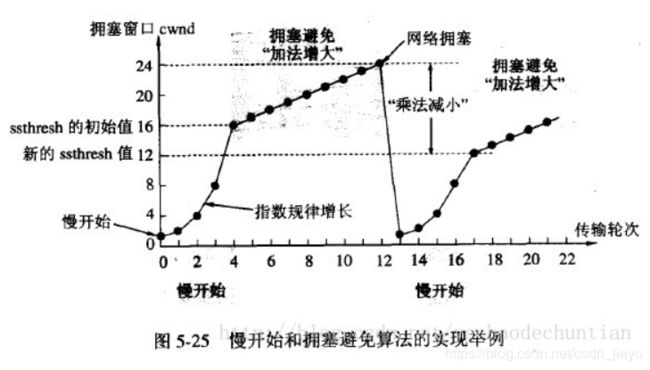
- 快重传和快恢复:接收方立即发送确认,而不是等到发送数据时才捎带确认;即使收到了失序的报文段,也要发送正确接收的报文段的重复确认;发送方一旦收到了三个连续的重复确认,就将相应的报文段立即重传;这就是所谓的快重传,而不会像慢开始那样,将拥塞窗口减小为1。发送方一旦受到三个连续的重复确认,就知道不是发生了拥塞,于是执行快恢复算法,即将慢开始门限值和拥塞窗口大小调整为当前框口的一半,然后执行拥塞避免算法。
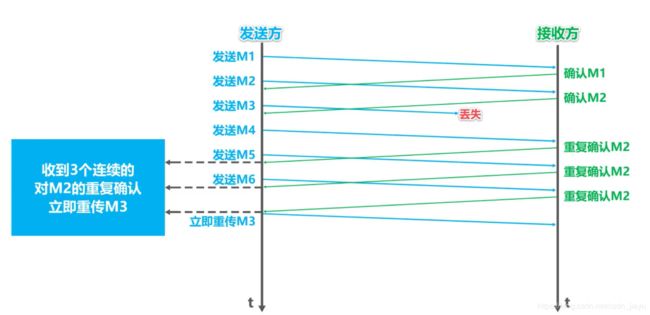
详见:计算机网络第35讲-TCP的拥塞控制(计算机网络简明教程及仿真实验)
7.TCP和UDP有什么区别?
- TCP要建立连接,而UDP不用建立连接。由此引出TCP和UDP另一个区别:TCP是点到点通信,只能一对一;而UDP既能一对一,又能一对多(比如直播)。
- TCP是可靠传输,保证数据无差错、无缺失、无重复、正确顺序;UDP是不可靠传输,只是尽最大努力交付就行,不管传输成不成功。
- TCP有拥塞控制,而UDP不管网络是否拥塞,只是一直发送。
- TCP面向字节流,而UDP面向报文。
- TCP首部开销20字节,UDP首部开销8字节。
一般来说判断是是TCP还是UDP就是一个数据包是否能发送完,如果能发送完就用UDP,不能就要分段并建立连接,用TCP。
8. 为什么TCP建立会话要三次握手?
首先说一下TCP三次会话都在干什么:
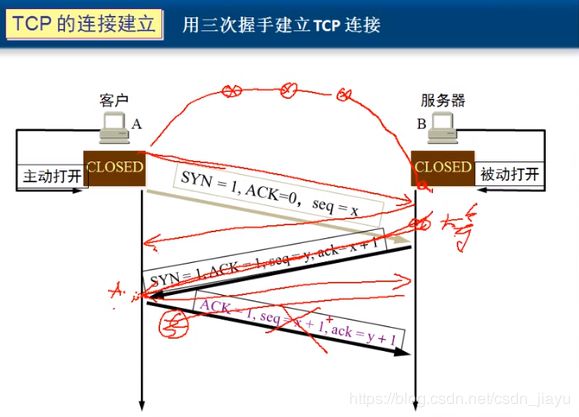
假设有A(客户端)想跟B(服务端)通话,那么A首先要给B发送一条信息,消息的内容为 S Y N = 1 , A C K = 0 , s e q = x SYN=1, ACK=0, seq=x SYN=1,ACK=0,seq=x(SYN=1表示要求建立联机,ACK是确认码,seq是序号),于是B给A回复确认 S Y N = 1 , A C K = 1 , s e q = y , a c k = x + 1 SYN=1, ACK=1, seq=y, ack=x+1 SYN=1,ACK=1,seq=y,ack=x+1(ack是确认号,表示A下一个该发的字节),A再给B一个确认 A C K = 1 , s e q = x + 1 , a c k = y + 1 ACK=1, seq=x+1, ack=y+1 ACK=1,seq=x+1,ack=y+1,这样就完成了三次握手。
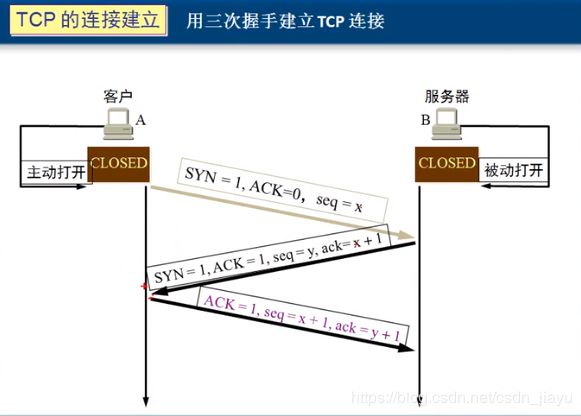
接下来讨论为什么要第三次确认:
假设只用两次握手就建立会话,那么假如A给B第一次发建立连接请求的时候绕了远路,A等了一段时间之后没有收到B的确认,就会再发一次连接请求,B收到A发的第二次请求后返回确认,A和B之间建立了会话。这时候B收到了A发的第一次建立连接请求,再返回确认给A,A已经收到过来自B的确认,所以丢掉了这次确认,而此时B以为已经建立了连接,所以等待A给自己进行通信,然后一直等,就会造成B计算机的资源浪费,所以要三次握手才能建立可靠连接。
9.四次挥手
首先A(客户端)给B(服务端)发送关闭连接请求 F I N = 1 , s e q = u FIN=1, seq=u FIN=1,seq=u(FIN=1表示关闭邻接请求,seq是序号),然后B给A返回确认 A C K = 1 , s e q = v , a c k = u + 1 ACK=1, seq=v, ack=u+1 ACK=1,seq=v,ack=u+1,这样A就不能给B发数据了。接下来B给A发送关闭连接请求 F I N = 1 , A C K = 1 , s e q = w , a c k = u + 1 FIN=1, ACK=1, seq=w, ack=u+1 FIN=1,ACK=1,seq=w,ack=u+1,A给B返回确认 A C K = 1 , s e q = u + 1 , a c k = w + 1 ACK=1, seq=u+1, ack=w+1 ACK=1,seq=u+1,ack=w+1。
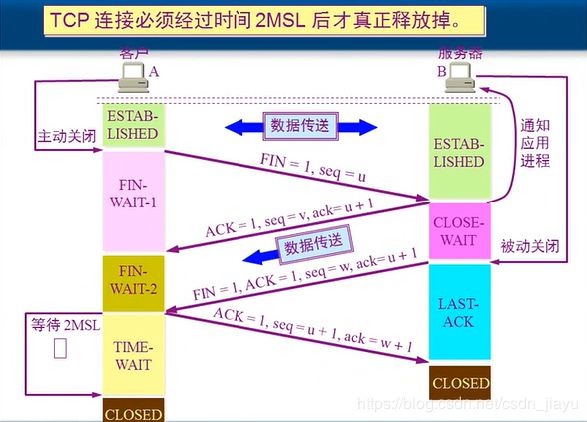
之所以要四次挥手,是为了保证数据传输能够完成。如果只完成前两次挥手,那么只是A不再给B发送数据了,B要发给A的数据可能还没传完。所以要B给A也发送确认关闭请求。另外,A给B确认之后,还要等待约2分钟时间,因为A发给B的确认可能丢失,B未收到确认会再发送一次关闭连接请求。
详见:计算机网络 韩立刚 p70
Python/C++
1.Python中is和==的区别?
is比较的是两个变量的地址是否相等,a is b实际调用的是id(a) == id(b);==比较的是两个变量的值,a == b调用的是a.__eq__(b)函数。所以对列表、字典、集合和元组is和==都不一样。但是数字和字符串存在特例:
数字
a = 10
b = 10
print(a is b) # True
c = 1000
d = 1000
print(c is d ) # False
Python[-5, 256]范围内的整型数字存储在一个叫small_int的链表里面,在Python的运行周期内不再创建新的对象,而是直接饮用缓存里的对象,所以上面a is b是True,c is d是False。
a = 'hello_world'
b = 'hello_world'
print(a is b) # True
c = 'hello world'
d = 'hello world'
print(c is d) # False
这是因为Python的字符串驻留机制,只有出现了非标识符允许的字符的时候才不采取驻留。
注:上面两段代码是在Python console中运行的结果,如果是作为脚本文件运行,那么结果全都是True。这是因为作为脚本文件运行时,Python将整个脚本当做一个代码块,运行d时发现c已经存在,就不再另外创建对象了。
2.Python中range和xrange的区别?
这个是在Python2中的,range返回的是一个列表,而xrange返回的是一个生成器,当需要生成一个很大的序列的时候,xrange的性能远远优于range,因为不需要一开始就开辟一块很大的空间。Python3中的range和Python2中的xrange类似,但Python3中的range实现了__contains__方法,查找时间一个元素是否在其中复杂度为O(1),而Python2中的xrange查找时间复杂度为O(n)。
3.Python多线程为什么是鸡肋?
主要是全局解释器锁,导致同一时刻只能有一个线程运行。
对于面向I/O的程序来说,在程序调用I/O的时候,GIL锁会被释放,让其他线程在这个线程等待I/O的时候运行。也就是说,I/O密集型的程序比计算密集型的程序更能利用Python多线程。
也可以用C语言写好计算密集型任务,然后做成动态链接库,让Python调用。调用过程中GIL锁也会被释放,从而做到多线程。
详见:为什么有人说 Python 的多线程是鸡肋呢?
4.Python赋值、浅拷贝和深拷贝的区别?
赋值是将对象的地址进行了传递,只生成了新的变量,没有生成新的对象。
浅拷贝生成了新的对象,但对象中元素还是指向原对象中元素的地址。
深拷贝不仅生成了新的对象,而且生成了新的元素。(例外:数字、字符串等类型不会生成新的元素)
详见:图解Python深拷贝和浅拷贝
5.python传参会改变参数值吗(python是值传递还是引用传递)?
首先明白一点,在python中,类型是属于对象的,变量没有类型。
例如:
foo = 3 // foo是一个变量,该变量指向int类型的对象3
bar = [3] // bar是一个变量,指向list类型的对象,该对象中包含一个int型数据3
python中有可变类型和不可变类型,可变类型例如list, dict, set等,不可变类型如string, tuple, numbers等。下面来看两个例子:
foo = 3
foo = 4
在上面的例子中,foo这个变量从指向int类型的对象3改为指向int类型的对象4,对象3并没有消失,而是在合适的时机由python负责清理
bar = [3]
bar[0] = 4
上面的例子中,一开始bar指向list类型的对象,这个对象中有一个int型数据3,后来将list对象中的数据3修改为了数据4。bar指向的list没变,但list中的内容变了。
接下来讨论参数传递:
def change_number(a):
a = 10
foo = 3
change_number(foo)
print(foo) // 结果是 3
在上述例子中,foo作为change_number的参数传入了函数,就是把a也指向了foo指向的int类型数据3,而a=10则是将a重新指向一个数据10,但是foo仍然指向int类型的数据3
再看另一个例子:
def change_list(a):
a[0] = 10
a = [15, 20]
bar = [3, 4]
change_list(bar)
print(bar) // 结果是[10, 4]
在上面的例子中,bar作为change_list的参数传入函数,也就是把a也指向了bar指向的list类型对象,a[0]=10是修改list对象中的int类型数据3为int类型数据10,所以bar指向的这个list对象变成了[10, 4];再接下来a = [15, 20]是将a指向了另外一个list类型对象,对bar指向的list类型对象没有影响。
6.Python装饰器?
装饰器本质上是一个类或函数,它可以让已经存在的函数或类在不经任何代码修改的情况下增加额外功能,装饰器的返回值也是一个函数/类。
例如为foo函数添加打印日志功能:
def use_log(func):
def wrapper():
logging.warn("%s is running" % func.__name__)
return func()
return wrapper
def foo():
print("I am foo")
foo = use_log(foo)
foo() # 执行foo()就相当于执行wrapper()
而在python语法糖中,可以省去foo = use_log(foo)这一句:
def use_log(func):
def wrapper():
logging.warn("%s is running" % func.__name__)
return func()
return wrapper
def foo():
print("I am foo")
@use_log
foo() # 执行foo()就相当于执行wrapper()
也可以有类装饰器,将内容写到__call__方法中去就行。
详见:理解 Python 装饰器看这一篇就够了
7.Python生成器?
Python函数中用yield关键字来返回值的时候,这种函数就叫生成器函数,函数被调用是返回一个生成器对象。
def fib(n):
prev, curr = 0, 1
while n > 0:
n -= 1
yield curr
prev, curr = curr, curr + prev
print([i for i in fib(10)])
#[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
详见:看完这篇,你就知道Python生成器是什么
8.C++的多态是什么?怎么实现的?
C++的多态就是在基类成员函数中加入virtual关键字,在派生类中重写该函数。运行时如果传入的是基类类型,就调用基类的成员函数;如果传入的是派生类类型,就调用派生类的成员函数。
对此,我们可以做一个实验:
#include
using namespace std;
class A
{
int i;
public:
A() :i(10) {}
virtual void fun() { cout << "A::fun " << i << endl; }
};
class B :public A
{
int j;
public:
B() :j(20) {}
virtual void fun() { cout << "B::fun " << j << endl; }
};
int main()
{
A a;
B b;
// 调用A的fun()
a.fun();
// 调用B的fun()
b.fun();
// a = b只是把b的值传给了a,没有改变a的类型,所以这里调用A的fun()
a = b;
a.fun();
// 指针p指向b的地址,b中存放的是B类型的实例,所以这里调用B的fun()
A* p=&b;
p->fun();
// 指针p指向a的地址,a中存放的是A类型的实例
// a = b只是把b的值传给了a,没有改变a的类型,所以这里调用A的fun()
a = b;
p = &a;
p->fun();
system("pause");
return 0;
}
输出:
A::fun 10
B::fun 20
A::fun 10
B::fun 20
A::fun 10
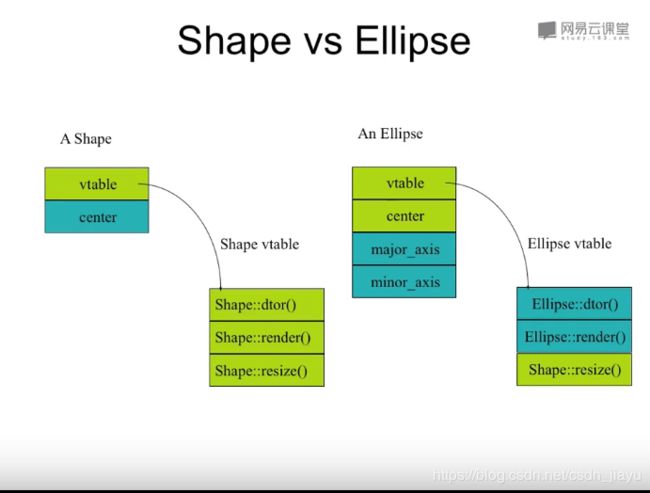
C++的所有特性都能用C语言实现,而多态的实现是因为在类里面多了一个指针,该指针指向一个虚表,里存放的是虚函数的地址,里面的每一项地址都指向一个虚函数的实现。子类可以继承虚表,如果子类没有重写虚函数,那么虚表里存放的就是父类虚函数的地址;如果子函数重写了虚函数,那么虚表里存放的就是子类虚函数的地址。
详见:【翁恺】面向对象程序设计_C++(浙江大学公开课)p23-p24
9.C++中的static、external、register这些关键字
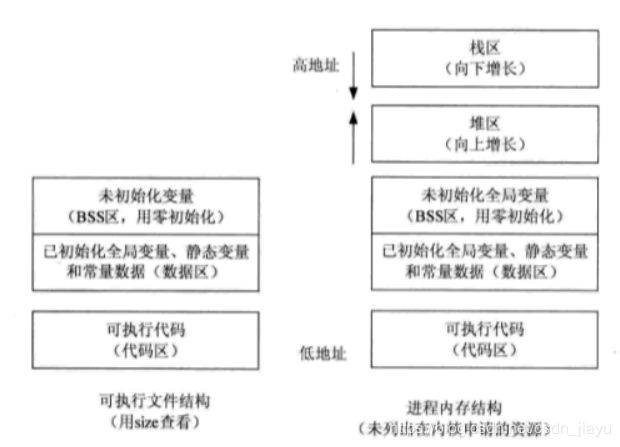
static的局部变量和全局变量都放在数据区中,静态局部变量作用域是{}代码块,静态全局变量作用域是本文件。
extern只用于全局变量:例如在文件a中定义并初始化变量i,在文件b中只需extern i就可以直接使用i。
register变量常驻于CPU的寄存器中,是用于加速运行的。
详见:C/C++堆区、栈区、常量区、静态数据区、代码区详解
另:C++中static:
静态成员变量是在类中加入static关键字,无论多少个实例,在内存中都只有一拷贝。而正常的成员变量是每个实例都有各自的内存拷贝。
静态成员函数时类中的成员加入static关键字,该成员函数属于类,不属于实例。
10.结构体占多少字节?
首先各种类型数据在内存中占字节数如下:
| char | short | int | float | double | 指针 |
|---|---|---|---|---|---|
| 1 | 2 | 4 | 4 | 8 | 4 |
同时还要考虑到对齐,例如:
struct Node
{
char a;
short b;
int c;
short d;
};
最大的int占字节数是4,所以按照4对齐:a占一个字节,从位置0开始;b占两个字节,从位置1开始,1不能整除2,所以先填充一个字节再用b占两个字节;c占4个字节,从位置4开始;d占两个字节,从位置8开始;到此为止一共10个字节,不整除4,所以添2个字节;最终一共占12个字节。
另:
(1)C++的结构体中,静态成员变量单独存放在数据区,不和结构体放在一起。
(2)如果结构体2中包含结构体1,那么结构体1的对齐参数是结构体1中对齐参数最大的类型的对齐参数(例如上面的结构体对齐参数是4),而不是结构体所占内存大小。
详见:C语言 - 结构体所占字节数
11.写一下lower_bound和upper_bound的实现。
// lower_bound和upper_bound的“right”值都应该是n而不是n-1,因为有可能x大于数组中所有数字
int lower_bound(int a [], int left, int right, int x)
{
while (left < right) // left==right时,就是第一个大于等于x的位置
{
int mid = (left + right) / 2;
if (a[mid] >= x) // 说明第一个大于等于x的数字一定在mid或mid左边
{
right = mid;
}
else // 第一个大于等于x的数字一定在mid右边
{
left = mid + 1;
}
}
return left; // 返回left或right都行
}
int upper_bound(int a[], int left, int right, int x)
{
while (left < right) // 当left==right时已经找到第一个大于x的数字
{
int mid = (left + right) / 2;
if (a[mid] > x) // 第一个大于x的数字一定在mid或mid左边
{
right = mid;
}
else // 第一个大于x的数字一定在x右边
{
left = mid + 1;
}
}
return left; // 返回right也行
}
12.指针和引用的区别?
指针是一个变量,存放的是另一个变量的地址;引用是类型别名。
指针可以由多级指针,而引用不能有多级引用;指针作为参数传递时,是拷贝了一个指针,这个指针和实参指向相同的地址;而引用直接操作指向的对象;此外,指针会分配内存,而引用不会另外分配内存。
详见:浅谈C++中指针和引用的区别
13.你用过哪些C++11的特性?
- auto
在C++11之前auto修饰的变量,是具有自动存储期的局部变量(事实上只要不声明为static的局部变量,都是具有自动存储期的);C++11开始,auto表示一个类型占位符,告诉编译器根据初始化表达式推断变量类型。 - 基于范围的for循环
例如string str; for (char c: str);表示遍历字符串str。 - lambda(匿名函数)
跟Python中的lambda表达式类似,例如:auto multiply = [](int a, int b) { return a * b; }; int product = multiply(2, 5); // 输出:10
详见:C++开发者都应该使用的10个C++11特性
14.sizeof和strlen的区别?
strlen是字符串的实际长度,从字符串第一个字符开始,直到找到’\0’为止;sizeof表示变量占用的内存。
#include
#include
int main()
{
char *str1 = "http://see.xidian.edu.cn/cpp/u/shipin/";
char str2[100] = "http://see.xidian.edu.cn/cpp/u/shipin_liming/";
char str3[5] = "12345";
printf("strlen(str1)=%d, sizeof(str1)=%d\n", strlen(str1), sizeof(str1));
printf("strlen(str2)=%d, sizeof(str2)=%d\n", strlen(str2), sizeof(str2));
printf("strlen(str3)=%d, sizeof(str3)=%d\n", strlen(str3), sizeof(str3));
return 0;
}
/*
运行结果:
strlen(str1)=38, sizeof(str1)=4
strlen(str1)=45, sizeof(str1)=100
strlen(str1)=53, sizeof(str1)=5
上面的运行结果,strlen(str1)=53显然不对,53是没有意义的。
*/
详见:C语言strlen()函数:返回字符串的长度
15.C++中的const关键字。
const主要用法:
(1)常量:
const int a=10;a作为常量使用,不可变;一定要在定义的时候就初始化。
(2)const和指针:
tip:判断指针是const还是指针指向的内容是const的,从右往左读,先读到const,说明指针是const的,即指针只能指向这块地址,不能指向别的地址,但地址里的值是可变的;先读到*,说明指针指向的内容是const的,不能通过指针来修改,可以把指针指向别的地址。
const int *p; // 指针指向的内容是const的
int const *p; // 指针指向的内容是const的
int* const p; // 指针是const的
(3)const修饰函数参数:一般用于参数是指针或者引用时,这样传入参数之后不用担心函数修改实参的值
(4)const成员函数:不允许成员函数修改成员变量。
(5)const函数返回值:不允许用户修改返回值。
详见博客:C/C++中const关键字详解
16.了解vector的实现吗?
vector内部其实相当于一个array,每次超过最大容量的时候就两倍扩容。其中有start、finish和end_of_storage,vector几乎所有操作都围绕这三个元素展开。
详见:序列容器之vector
17.getline的用法
getline有两种用法:
-
一种作为输入流istream的成员函数,包括两种重载形式:
istream& getline(char* s, streamsize n) istream& getline(char* s, streamsize n, char delim)前者表示读入字符串s的前n个字符,后者表示读入字符串s的前n个字符直到定界符delim。
-
另一种是作为里的一个普通函数,有四种重载形式
istream& getline (istream& is, string& str, char delim); istream& getline (istream&& is, string& str, char delim); istream& getline (istream& is, string& str); istream& getline (istream&& is, string& str);读入一个输入流(比如cin),用str存储输入流中的信息,默认定界符是’\n’,也可以自己输入定界符。
-
最后说一下
while(getline(cin, str)),这个函数会一直读入,直到文件结束/遇到函数定界符/输入达到最大限度。
详见博客:C++ getline()函数的用法
18.重写与重载的区别?
重写是父类中定义虚函数,子类中重新定义相同名称和参数的函数,起到多态的作用。重载是定义若干个名称相同的函数,它们的参数类型、参数顺序、参数量至少有一项不同,返回值可以相同可以不同。
PS:重定义相当于继承中的重载。
详见:C++_重载、重写和重定义的区别
19.define和const的区别?
- define没有类型检查,只是字符替换,而const有类型检查,所以一般用const。
- define可以定义表达式,而const不可以。
详见:
const常量与define宏定义的区别
20. 结构和联合的区别?
也就是结构体和联合体的区别。
结构体是构造一种数据类型,把不同的数据类型组合成一个整体,其中的各个成员独立存在,所以结构体所占内存是各成员变量所占内存长度之和;成员之间的赋值也各不影响。
联合体是把几个不同类型的数据共用一段内存,所以联合体所占内存等于最大的成员所占内存的长度;对其中一个成员赋值,其他成员的值会被重写,原来的值就不存在了。
详见:【C/C++】结构体和联合体的区别
21.C++单例模式了解吗?
单例模式是保证一个类只有一个实例,并提供一个全局访问点,该实例被所有程序模块共享。
在C++中,可以使用类的私有静态指针变量指向类的唯一实例,并用一个公有的静态方法获取该实例。
class CSingleTon
{
private:
CSingleTon(){} // 构造函数是私有的
static CSingleTon* m_pInstance; // 私有的静态指针变量
public:
static CSingleTon* getInstance()
{
if (m_pInstance == nullptr) // 第一次调用
m_pInstance = new CSingleTon();
return m_pInstance;
}
};
详见:C++中的单例模式
Linux/Spark
1.查看进程的命令?
创建:fork
查看:ps a
杀进程:kill xxx
2.在linux某个文件中搜索?
grep 字符串 文件名
数学/思维
1.一个骰子,6面,1个面是 1, 2个面是2, 3个面是3, 问平均掷多少次能使1,2,3都至少出现一次?
凡是这种类似的求期望的题,都采用“分叉树递归列方程法”。
详见:求解概率问题的神器——分叉树递归列方程法
2.给10x10的棋盘,扫雷,随机放置10个点作为雷,如何保证随机放置?
将x个雷放入y个格子中,每个格子放入雷的概率等于剩下的雷/剩下的格子,这样能保证比较均匀。
3.有54张牌,分3组,大王小王同在一组的概率?
P = C 3 1 C 52 16 C 36 18 C 18 18 C 54 18 C 36 18 C 18 18 = 3 ∗ 52 ∗ 51 ∗ . . . ∗ 37 1 ∗ 2 ∗ . . . ∗ 16 54 ∗ 53 ∗ . . . ∗ 37 1 ∗ 2 ∗ . . . ∗ 18 = 17 53 P=\frac{C_{3}^{1}C_{52}^{16}C_{36}^{18}C_{18}^{18}} {C_{54}^{18}C_{36}^{18}C_{18}^{18}} =\frac{3*\frac{52*51*...*37}{1*2*...*16}} {\frac{54*53*...*37}{1*2*...*18}} =\frac{17}{53} P=C5418C3618C1818C31C5216C3618C1818=1∗2∗...∗1854∗53∗...∗373∗1∗2∗...∗1652∗51∗...∗37=5317
4.站在地球上的某一点,向南走一公里,然后向东走一公里,最后向北走一公里,回到了原点。地球上有多少个满足这样条件的点?
只要找到一个点,这个点向东走1公里后回到原点就满足条件。维度线长度为1公里的维度上,任意一个点都满足。
还有一个特例:从北极点出发,走一个等边三角形。
5.一个四位数abcd,满足abcd * 4 = dcba,求这个数。
(1) 4 a = d 4a=d 4a=d没有进位,所以 a = 1 a=1 a=1或 a = 2 a=2 a=2;又 4 d % 10 = a 4d\%10=a 4d%10=a,所以 a a a只能为 2 2 2,对应 d = 8 d=8 d=8
(2)根据(1)有 ( 4 c + 3 ) % 10 = b (4c+3)\%10=b (4c+3)%10=b且 4 b < c < 10 4b
(3)若 b = 0 b=0 b=0,没有 c c c能满足(2)
\quad\quad 若 b = 1 b=1 b=1, c = 7 c=7 c=7时满足2
\quad\quad 若 b = 2 b=2 b=2,没有 c c c能满足(2)
(4)综上,abcd=2178
6.一个圆上随机三个点组成锐角三角形的概率?
假设圆心是O,圆上有A、B两个点。假设 A A A在坐标轴 x x x上,分两种情况讨论:(1) ∠ A O B ∈ ( 0 , π ) \angle AOB \in (0, \pi) ∠AOB∈(0,π) (2) ∠ A O B ∈ ( π , 2 π ) \angle AOB \in (\pi, 2\pi) ∠AOB∈(π,2π)
对于第一种情况,连接并延长AO交圆与 A ′ A^{'} A′,连接并延长BO交圆与 B ′ B^{'} B′,如果C在弧 A ′ B ′ A^{'}B^{'} A′B′上,则三角形ABC是锐角三角形,否则三角形ABC是钝角三角形。
∫ 0 π ∫ π θ B + π P ( θ B ) P ( θ C ) d θ C d θ B = ∫ 0 π ∫ π θ B + π 1 2 π 1 2 π d θ C d θ B = 1 4 π 2 ∫ 0 π θ B d θ B = 1 8 \int_0^\pi \int_\pi^{\theta_B+\pi} P(\theta_B) P(\theta_C) \ d\theta_C d\theta_B\\ =\int_0^\pi \int_\pi^{\theta_B+\pi} \frac{1}{2\pi}\frac{1}{2\pi}\ d\theta_C d\theta_B\\ =\frac{1}{4\pi^2} \int_0^\pi \theta_B\ d\theta_B\\ =\frac{1}{8} ∫0π∫πθB+πP(θB)P(θC) dθCdθB=∫0π∫πθB+π2π12π1 dθCdθB=4π21∫0πθB dθB=81
同理,第二种情况也是 1 8 \frac{1}{8} 81,所以圆上任选三点组成锐角三角形的概率是 1 4 \frac{1}{4} 41。
7.100个人坐100个座位,第一个人随机坐,后面每个人如果能做自己的座位就坐自己的座位,不能的话就随机坐,问第100个人坐自己的座位的概率?
1)第一个人随机坐,第二个人不能坐自己的座就随机坐(2)第一个人随机坐,第二个人坐自己的座位,如果发现第一个人在自己的座位上,就让第一个人去随机坐
(1)、(2)两种方案对第三个人来说其实是没有区别的。所以第2~99个人最终都能坐在自己的座位上,第一百个人坐的时候第一个人可能在100也可能在1,所以第一个百个人坐在自己座位的概率是 1 2 \frac{1}{2} 21
项目相关
注:简历上的每一句话都是你要展示的内容,凡是写上简历的,一定要做到完全熟悉。
1.文字检测项目有什么不错的做法和创新?
- 数据扩增部分除了用到旋转、裁剪、翻转这些操作,由于基础网络是用的FCN,所以输入图片可以是任意大小,于是做了将图片从128*128到768*768每次增大128像素。不进行该数据扩增,valid_loss在0.54左右,做了数据扩增之后降到0.33左右。(从别的论文上看到的这个做法)
- 测试时发现尺寸较大的图比尺寸小的图检测效果好,所以测试时在输入之前先调整图片大小,再送入测试。
2.谈谈深度学习发展
- Alexnet在2012年引爆了深度学习领域,主要亮点是用了ReLU函数和Dropout
- 2014年VGG16使用的都是3*3小卷积核,2个3*3卷积核效果好于1个5*5卷积核,前者用了两次激活函数,带来了更多的非线性变换,分类效果更好,且参数量更小。作者还试用了1*1卷积核,1*1卷积主要作用是改变通道数。同时1*1卷积专注于通道间的特征组合,而3*3卷积同时关注局部信息整合和通道间信息整合。
- 同年GoogleNet(Inception)与以往增加网络深度的模型不同,GoogleNet专注于增加网络宽度,即把1*1、1*1后3*3、1*1后5*5、3*3后1*1的结果拼接起来,在降低参数量的同时提取到不同尺度的特征。
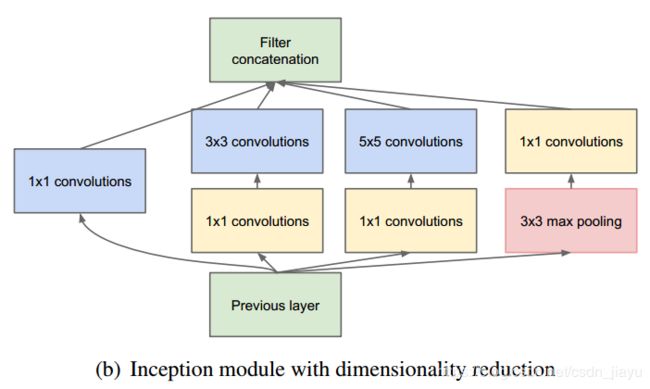
- 2015年的残差网络主要是加入了残差连接,减轻了随着层数加深出现的网络退化问题。
3.文字检测部分网络用的损失函数是什么?
整个Loss分为三部分,分别是:(1)像素点是否在框内(2)像素点是前点还是后点(3)像素点如果是前点,到(x0, y0)、(x1, y1)的距离;像素点如果是后点,到(x2, y2)、(x3, y3)的距离。
L o s s = 4 L i n s i d e + L v e r t e x + L q u a d Loss=4L_{inside}+L_{vertex}+L_{quad} Loss=4Linside+Lvertex+Lquad
(1)
L i n s i d e = − β Y l o g Y ^ − ( 1 − β ) ( 1 − Y ) l o g ( 1 − Y ^ ) L_{inside}=-{\beta}Ylog{\hat{Y}}-(1-\beta)(1-Y)log(1-\hat{Y}) Linside=−βYlogY^−(1−β)(1−Y)log(1−Y^)
其中 β \beta β表示负样本占总数的比值
(2)
L v e r t e x = ( − β v Y v l o g Y ^ v − ( 1 − β v ) ( 1 − Y v ) l o g ( 1 − Y ^ v ) ) ∗ p w e i g h t s ∑ i = 1 b a t c h _ s i z e ∗ H / 4 ∗ W / 4 p w e i g h t s i L_{vertex}=\frac{(-\beta_{v}Y_vlog\hat{Y}_v-(1-\beta_v)(1-Y_v)log(1-\hat{Y}_v))*p_{weights}}{\sum_{i=1}^{batch\_size*H/4*W/4}p_{weights_i}} Lvertex=∑i=1batch_size∗H/4∗W/4pweightsi(−βvYvlogY^v−(1−βv)(1−Yv)log(1−Y^v))∗pweights
其中 β v \beta_{v} βv表示是框内的点的像素中不是前后点的占比; Y v {Y}_v Yv表示是一个两通道的向量,两个通道分别表示是否前后点以及是前点还是后点; p w e i g h t s p_{weights} pweights表示标签的第一个通道。
(3)
L q u a d = s m o o t h _ L 1 _ l o s s ( Y q u a d , Y ^ q u a d ) ∗ v w e i g h t s 4 ∗ N q ∗ ∑ i = 1 b a t c h _ s i z e ∗ H / 4 ∗ W / 4 v w e i g h t s i L_{quad}=\frac{smooth\_L1\_loss(Y_{quad}, \hat{Y}_{quad})*v_{weights}}{4*N_q*\sum_{i=1}^{batch\_size*H/4*W/4}v_{weights_i}} L