NEFU 大一寒假训练五（GCD&&快速幂）2020.01.04

Summary

昨天的题目预测命中率90%（9/10）还算可以吧
今天的题难度直线上升，真的是让熊头大 (　o=^•ェ•)o　┏━┓

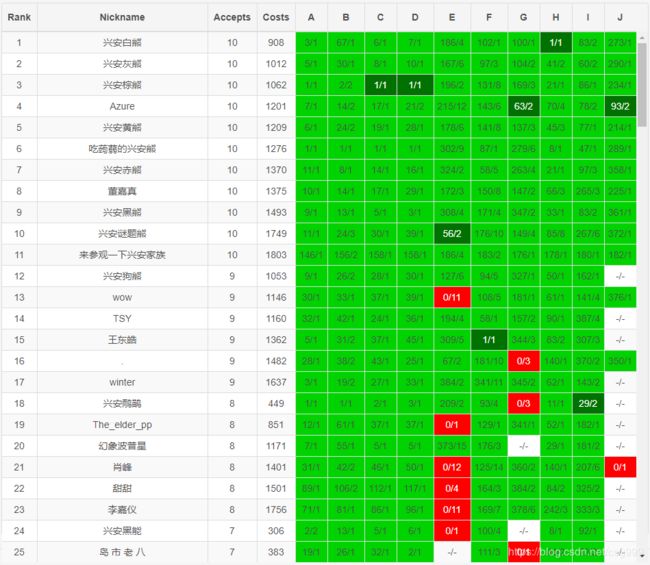
Information

No.	Title	AC/Submit
A	最大公约数和最小公倍数	141/168
B	又见GCD	136/283
C	多个数的最大公约数	137/197
D	多个数的最小公倍数	131/175
E	LCM&GCD	25/314
F	人见人爱gcd	80/436
G	高木同学的因子	21/162
H	快速幂取模	103/236
I	库特的数学题	41/139
J	异或方程解的个数	17/24

Problem A: 最大公约数和最小公倍数 (1077) [141/168]

Tips

算是一个gcd，lcm的模板题吧
lcm(x,y)=x/gcd(x,y)*y

Code

#include 
using namespace std;

int gcd(int a,int b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	int a,b,ans;
	while(cin>>a>>b)
	{
		ans=gcd(a,b);
		cout<<ans<<" "<<a/ans*b<<endl;
	}
	return 0;
}

Problem B: 又见GCD (992) [136/283]

Tips

gcd应用，也不是难题

Code

#include 
using namespace std;

int gcd(int a,int b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	int a,b,i,j;
	while(cin>>a>>b)
	{
		i=b;
		j=1;
		while(gcd(a,i)!=b||b==i)
		{
			i=b*j++;
		}
		cout<<i<<endl;
	}
	return 0;
}

Problem C: 多个数的最大公约数 (764) [137/197]

Tips

多重gcd

Code

#include 
using namespace std;

long long gcd(long long a,long long b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	int n;
	long long a,ans;
	while(cin>>n)
	{
		cin>>ans;
		n--;
		while(n--)
		{
			cin>>a;
			ans=gcd(a,ans);
		}
		cout<<ans<<endl;
	}
	return 0;
}

Problem D: 多个数的最小公倍数 (765) [131/175]

Tips

多重lcm

Code

#include 
using namespace std;

long long gcd(long long a,long long b)
{
	return b?gcd(b,a%b):a;
}

long long lcm(long long a,long long b)
{
	return a/gcd(a,b)*b;
}

int main()
{
	int n;
	long long a,ans;
	while(cin>>n)
	{
		cin>>ans;
		n--;
		while(n--)
		{
			cin>>a;
			ans=lcm(a,ans);
		}
		cout<<ans<<endl;
	}
	return 0;
}

Problem E: LCM&GCD (1411) [25/314]

Tips

本来以为需要算法优化，结果发现还是暴力香~
直接两层for会超时，那么可以用一层for找出中间的一个数i，再用x*y/i得到另一个数，原理如下：
设中间两个数分别为i和j 根据题目要求可得gcd(i,j)=x lcm(i,j)=y
又因为lcm(i,j)=i*j/gcd(i,j) 所以可以得到 i*j=x*y

Code

#include 
using namespace std;

int gcd(int a,int b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	ios::sync_with_stdio(false);
	long long t,x,y,ans,g,xy,j;
	cin>>t;
	while(t--)
	{
		cin>>x>>y;
		xy=x*y;
		ans=0;
		for(int i=x;i<=y;i+=x) //因为x是ij的最大公约数所以i和j都能被x整除，所以可以用i+=x减少循环次数
		{
			if(xy%i!=0)continue; //不能整除时不符合要求
			j=xy/i;
			g=gcd(i,j);
			if(g==x&&i/g*j==y)ans++;
		}
		cout<<ans<<endl;
	}
	return 0;
}

Problem F: 人见人爱gcd (1221) [80/436]

Tips

有一个神奇的地方就是gcd(x,y)=gcd(a,b)通过观察发现
除此之外这道题还比较坑，使用cin cout会超时
可以通过scanf() printf()解决

两次提交只是吧cin cout 换成了scanf printf 其他部分都没有修改

Code

#include 
using namespace std;

long long gcd(long long a,long long b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	long long t,a,b,ans;
	while(scanf("%lld",&t)!=-1)
	{
		while(t--)
		{
			//cin>>a>>b;
			scanf("%lld %lld",&a,&b); 
			ans=a*a-2*gcd(a,b)*b;
			printf("%lld\n",ans);
			//cout<
		}
	}
	return 0;
}

Problem G: 高木同学的因子 (1669) [21/162]

Tips

自从上面的F题超时了，我就在百度上找到了一段神奇的好东西：ios::sync_with_stdio(false);
所以今天后做的题目基本上都带这个防止读入输出超时，具体原理可以百度了解一下
这个题的难度有点大，直接跑会超时，那么就需要想其他的方法优化
思路就是将gcd(x,y)进行分解，分解成多个质数，再通过排列组合的方式输出获得答案
比如说样例的12和36最大公约数是12 将它分解成2 2 3，对于2有3种取法：取1个，取2个和不取，对于3则有2种取法。这样最终的答案就是2*3=6种。
代码写的不太好，可以优化一下分解过程，不用x,y同时分解。
另外需要注意gcd(x,y)=1的情况，此时ans*=yznum+1会得到2

Code

#include 
using namespace std;

long long gcd(long long a,long long b)
{
	return b?gcd(b,a%b):a;
}

int main()
{
	ios::sync_with_stdio(false); //加快cin cout输入输出
	long long yz[10000],yp=0,yznum; //yz[]质因子数组 yp质因子个数
	long long x,y,k,ans=0;
	cin>>x>>y;
	k=gcd(x,y);
	if(k==1)
	{
		cout<<1;
		return 0;
	}
	for(int i=2;i<=k;i++)
	{
		if(x%i==0&&y%i==0)
		{
			yz[yp++]=i;
			x/=i;
			y/=i;
			i=1;
			k=gcd(x,y);
			if(x==1||y==1)break;
			continue;
		}
	}
	ans=1;
	yznum=1; //相同因子数量
	for(int i=1;i<yp;i++)
	{
		if(yz[i]==yz[i-1])
		{
			yznum++;
		}
		else
		{
			ans*=yznum+1;
			yznum=1;
		}
	}
	ans*=yznum+1; //处理最后一组因子
	cout<<ans<<endl;
	return 0;
}

Problem H: 快速幂取模 (601) [103/236]

Tips

一道模板题

Code

#include 
using namespace std;

int main()
{
	long long a,b,c,ans;
	while(cin>>a>>b>>c)
	{
		ans=1;
		while(b>0)
		{
			if(b&1)ans=ans*a%c;
			a=a*a%c;
			b>>=1;
		}
		cout<<ans<<endl;
	}
	return 0;
}

Problem I: 库特的数学题 (1666) [41/139]

Tips

通过找规律可以发现 a[1]=2x3 a[2]=2x3² a[3]=2²x3²+2x3²=2x3³
因此得出公式a[n]=2x3ⁿ 其中3ⁿ部分用快速幂处理，最后在乘上2即可

Code

#include 
using namespace std;

int main()
{
	long long n,ans=1,num=3;
	cin>>n;
	while(n>0)
	{
		if(n&1)ans=ans*num%1000000007;
		num=num*num%1000000007;
		n>>=1;
	}
	ans=ans*2%1000000007;
	cout<<ans;
	return 0;
}

Problem J: 异或方程解的个数 (1834) [17/24]

Tips

这是一道纯数学题，与二进制有关 (下面的 ^是异或，不是n的x次幂)
观察题中所给的方程n−(n^x)−x=0，将其移项得到n−x=n^x
因此可以通过观察二进制发现一些规律
我们需要使n^x得到的值等于n-x的值，对每一位二进制来说1^0=1 1^1=0
如果通过二进制异或来进行减法运算，只需要使它异或上
例如n=2₍₁₀₎=10₍₂₎可以通过异或将二进制位中的1去掉实现减法的目的
这样x的取值可以是x=10₍₂₎=2₍₁₀₎此时2^2=0=2-2或者x=00₍₂₎=0₍₁₀₎此时0-0=0=0^0一共两种可能的取值
因此最终答案即为2的(n二进制位中1的个数)次幂 即2^{n二进制位中1的个数}

Code

#include 
using namespace std;

int main()
{
	ios::sync_with_stdio(false);
	unsigned int n,k,b1;
	while(cin>>n)
	{
		k=n;
		b1=0;
		while(k>0)
		{
			if(k&1)b1++;
			k>>=1;
		}
		cout<<(long long)pow(2,b1)<<endl;
	}
	return 0;
}