Codeforces Round #635 (Div. 2) A~D
https://codeforces.com/contest/1337/
A. Ichihime and Triangle
题意
给定四个数字 \(a,b,c,d(1\le a\le b\le c\le d\le 1e9)\),请给出任意一组满足下述条件的 \(x,y,z\) 。
- \(a\le x\le b \le y\le c \le z \le d\)
- \(x,y,z\) 可以构成三角形
解题
当 \(y=z=c\) 时,\(x\) 取 \([a,b]\) 中任意值都可以组成一个等腰三角形。
for i in range(int(input())):
a,b,c,d = list(map(int,input().split()))
print(b,c,c)
B. Kana and Dragon Quest game
题意
你在打一个血量为 \(x\) 的boss,你现在有两种技能可以释放。
- 技能一 Void Absorption:
- 当boss血量为 \(h\) 时,释放此技能可以使boss血量变成 \(\lfloor \frac{h}{2} \rfloor + 10\)
- 技能二 Lightning Strike
- 打击boss造成10点伤害,即 \(h-10\)
给出一个血量 \(x\) ,以及可以释放技能一的次数 \(n\) 和技能二的次数 \(m\),询问能否杀死boss。
解题
以贪心的方法考虑,当boss血量越高使用技能一打出的效果越好,所以我们的方案是优先尽可能的把技能一打出,再打出剩下的 \(m\) 个技能二。需要注意的是,当boss血量小于等于20时,技能一就无法造成伤害了,甚至成了回血技。
for i in range(int(input())):
x,n,m = list(map(int,input().split()))
while n>0 and x>20:
x = x//2+10
n-=1
while m>0 and x>0:
x-=10
m-=1
print("YES" if x<=0 else "NO")
C. Linova and Kingdom
题意
有 \(n\) 个城市,编号从 \(1\) 到 \(n\) ,其中 \(1\) 为首都。在这些城市中有 \(n-1\) 条双向道路,可以连通两个城市,保证每两个城市之间都存在的唯一的路径可以相互到达,即这是一个全连通的图。
给定一个 \(k\) ,你需要从 \(n\) 个城市中选出 \(k\) 个城市发展工业,其余的城市发展旅游业。每年每个工业城市都会派出一个代表,前往首都,在去的路上代表每经过一个旅游城市就会贡献 \(1\) 点满意度,询问你可以得到的最大的满意度和是多少。
解题
这是一道大毒瘤题,通过人数不及上一题1/2(悲
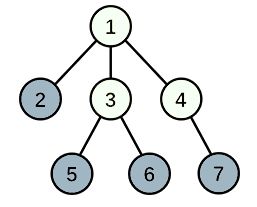
首先边为 \(n-1\) 的全连通图,说明这是一颗树,我们设编号 \(1\) 的节点为根。
对于一个城市来说,设需要经过他到达首都的其他城市到的数量为 \(ct\),即这个节点下面的子孙节点个数。设他到达首都需要经过的城市个数,即这个节点的深度 \(depth\),首都的深度为 \(0\) 。
当把一个城市选做为工业城市,那么这个城市对满意度的贡献度 \(v = depth - ct\) 。
选取贡献度最大的 \(k\) 个城市作为工业城市即可。
#include
#define ll long long
#define fr(i,n) for(int i=0;i=j;i--)
#define frrs(i,j,n,flag) for(int i=j;i=j&&flag;i--)
#define arend(i,n) ((i!=n-1)?" ":"\n")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<>a;return a;}
string to_str(double a) {stringstream ss;ss<e; //边
}nodes[2*e5];
int dfs(int i,int last){
int ct = 0;
nodes[i].depth = nodes[last].depth+1;
for(auto it:nodes[i].e) if(it!=last) ct+=dfs(it,i);
nodes[i].v = nodes[i].depth - ct;
return ct+1;
}
int main(){
cin.tie(0);
//ios::sync_with_stdio(false);
//cout<>n>>k){
frr(i,1,n+1){
nodes[i].i = i;
nodes[i].v = 0;
nodes[i].e.clear();
}
fr(i,n-1){
int a,b;cin>>a>>b;
nodes[a].e.push_back(b);
nodes[b].e.push_back(a);
}
nodes[0].depth = -1;
dfs(1,0);
ll ans = 0;
nth_element(
nodes+1,nodes+k+1,nodes+n+1,
[](node a,node b){
return a.v>b.v;
}
);
frr(i,1,k+1) ans += nodes[i].v;
cout< D. Xenia and Colorful Gems
题意
有三个长度分别为 \(n_r,n_g,n_r\) 的正整数数组 \(r,g,b\),其中 \(1\le r_i,g_i,b_i\le1e9\) 。
询问 \((r_i-g_j)^2+(r_i-b_k)^2+(g_j-b_k)^2\) 的最小值。
解题
同样是一道毒瘤题,通过人数接近B题的1/4。
三个 \(n\) 的范围上限 \(1e5\) ,很明显这是一道复杂度 \(O(nlogn)\) 的二分题。
如果想得到最小的 \((r_i-g_j)^2+(r_i-b_k)^2+(g_j-b_k)^2\) ,只需要让 \(r_i,g_j,b_k\) 的取值足够接近就可以了。
这里分类讨论6种情况:
- \(r_i\le g_j \le b_k\)
- \(r_i\le b_k \le g_j\)
- \(g_j \le r_i \le b_k\)
- \(g_j \le b_k \le r_i\)
- \(b_k \le r_i \le g_j\)
- \(b_k \le g_j \le r_i\)
对6钟情况分别考虑,在每种情况中遍历第二个数组,再对另外两个数组二分查找。在满足式子的值中,找出最接近遍历数字的值。
值得一提的是 lower_bound 会得到在值大于等于查询值的位置中,最小的一个。upper_bound 会得到值大于查询值的位置中,最小的一个,他的前一个位置一定是值小于等于查询值的位置中最大的,刚好满足我们的需求。
#include
#define ll long long
#define fr(i,n) for(int i=0;i=j;i--)
#define frrs(i,j,n,flag) for(int i=j;i=j&&flag;i--)
#define arend(i,n) ((i!=n-1)?" ":"\n")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<>a;return a;}
string to_str(double a) {stringstream ss;ss<
int nr, ng, nb;
ll ans;
ll p2(ll x){return x*x;}
void solve(Array a,Array b,Array c){
for(auto y:b){
auto px = upper_bound(a.begin(),a.end(),y);
auto pz = lower_bound(c.begin(),c.end(),y);
if(px==a.begin()||pz==c.end()) continue;
ll x = *(--px),z = *pz; //x<=y<=z 已经找到满足式子的最与y接近的x,z
ll res = p2(x-y) + p2(y-z) + p2(x-z);
if(ans>res||ans==-1) ans = res;
}
}
int main(){
cin.tie(0);
//ios::sync_with_stdio(false);
//cout<>t){
while(t--){
cin>>nr>>ng>>nb;
Array r(nr),g(ng),b(nb);
#define sortit(arr) sort(arr.begin(),arr.end())
fr(i,nr) cin>>r[i]; sortit(r);
fr(i,ng) cin>>g[i]; sortit(g);
fr(i,nb) cin>>b[i]; sortit(b);
ans = -1;
solve(r,g,b); solve(r,b,g);
solve(g,b,r); solve(g,r,b);
solve(b,r,g); solve(b,g,r);
cout<