线性回归模型 - python实现方法
1. 一元线性回归
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#导入线性回归模块
from sklearn.linear_model import LinearRegression
rng=np.random.RandomState(1) #随机种子
#生成随机数据x和y
xtrain=10*rng.rand(30)
ytrain=8+4*xtrain+rng.rand(30)
#样本关系:y=8+4x
fig=plt.figure(figsize=(12,3))
ax1=fig.add_subplot(1,2,1)
plt.scatter(xtrain,ytrain,marker='.',color='k')
plt.grid()
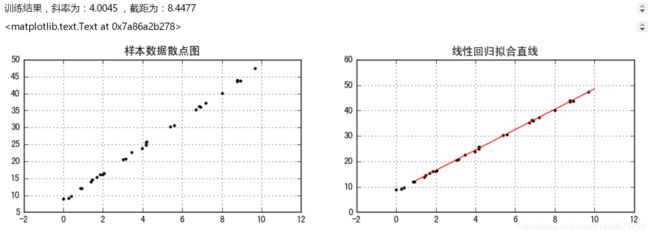
plt.title('样本数据散点图')
#线性回归模型
xtrain[:,np.newaxis]#将xtrain转化为列向量
model=LinearRegression() #构建回归模型
#训练模型
model.fit(xtrain[:,np.newaxis],ytrain)
#训练结果
model.coef_ #斜率
model.intercept_ #截距
print('训练结果,斜率为:%.4f ,截距为:%.4f' %(model.coef_,model.intercept_))
#输出拟合直线
#测试结果
xtest=np.linspace(1,10,100) #1-10,取100个值,测试值x
ytest=model.predict(xtest[:,np.newaxis]) #预测值
#作图
ax2=fig.add_subplot(1,2,2)
plt.scatter(xtrain,ytrain,marker='.',color='k')#拟合前的样本散点图
plt.plot(xtest,ytest,color='r')#拟合后的直线
plt.grid()
plt.title('线性回归拟合直线')
#误差
rng=np.random.RandomState(2)
xtrain=10*rng.rand(15)
ytrain=8+4*xtrain+rng.rand(15)*30
model.fit(xtrain[:,np.newaxis],ytrain)
#创建样本数据并进行拟合
xtest=np.linspace(0,10,1000)
ytest=model.predict(xtest[:,np.newaxis])
#作图
plt.plot(xtest,ytest,color='r',linestyle='--') #拟合直线
plt.scatter(xtrain,ytrain,marker='.',color='k') #样本数据散点图
ytest2=model.predict(xtrain[:,np.newaxis]) #样本数据x在拟合直线上的y值
plt.plot([xtrain,xtrain],[ytrain,ytest2],color='gray') #误差线
plt.grid()
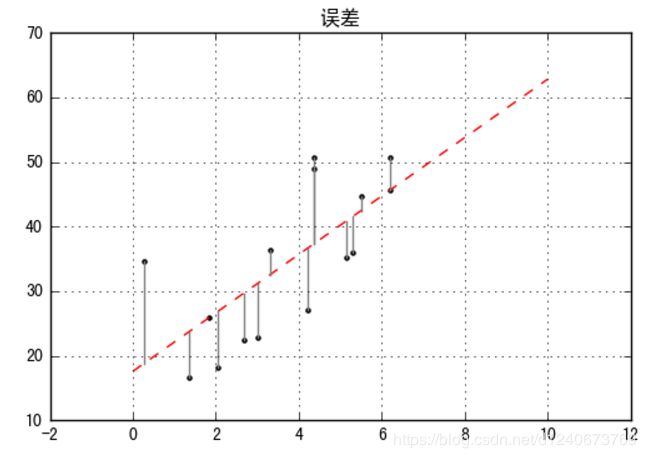
plt.title('误差')
2. 多元线性回归
rng=np.random.RandomState(5)
xtrain=10*rng.rand(150,4)
ytrain=20+np.dot(xtrain,[1.5, 2, -4, 3])
df=pd.DataFrame(xtrain,columns=['b1','b2','b3','b4'])
df['y']=ytrain
df.head()
#作图,查看变量是否相关
pd.scatter_matrix(df[['b1','b2','b3','b4']], figsize=(10,6),
diagonal='kde',
alpha=0.5,
range_padding=0.1)
#模型
model=LinearRegression()
model.fit(df[['b1','b2','b3','b4']],df['y'])
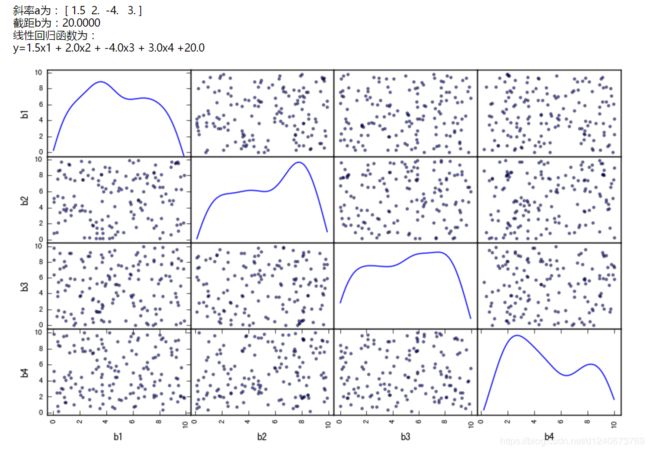
print('斜率a为:',model.coef_)
print('截距b为:%.4f' % model.intercept_)
print('线性回归函数为:\ny=%.1fx1 + %.1fx2 + %.1fx3 + %.1fx4 +%.1f'
% (model.coef_[0],model.coef_[1],model.coef_[2],model.coef_[3],model.intercept_))
3. 模型评估
通过几个参数验证回归模型
SSR:预测数据与原始数据均值之差的平方和
SST:原始数据和均值之差的平方和
SSE(和方差、误差平方和)
R-square(确定系数):SSR和SST的比值,确定系数是通过数据的变化来表征一个拟合的好坏,取值范围为[0,1],
越接近1,表名方程的变量对y的解释能力越强,这个模型对数据拟合的比较好
MSE(均方差、方差):该统计参数是预测数据和原始数据对应点误差的平方和的均值,也就是SSE/n,和SSE没有太大的区别
RMSE(均方根、标准差):回归系数的拟合标准差,是MSE的平方根
#模型评价
#MSE, RMSE,R-square
from sklearn import metrics
rng=np.random.RandomState(1)
xtrain=10*rng.rand(30)
ytrain=8+4*xtrain+rng.rand(30)*3
model=LinearRegression()
model.fit(xtrain[:,np.newaxis],ytrain)
ytest=model.predict(xtrain[:,np.newaxis])
mse=metrics.mean_absolute_error(ytrain,ytest)
rmse=np.sqrt(mse)
print(mse)
print(rmse)
ssr=((ytest-ytrain.mean())**2).sum()
sst=((ytrain-ytrain.mean())**2).sum()
r2=ssr/sst
print(r2)
#r2的另一种算法,通常用这种方法
r2=model.score(xtrain[:,np.newaxis],ytrain)
print(r2)
#模型评估一般比较r2参数即可,多个回归模型比较时,也可以比较mse,mse越小,越好,r2越接近1越好
#一般r2大于0.6都可以接收