谈韩信点兵问题

谈韩信点兵问题

　　数学的解题，包括问题、答案、求得答案的思路过程,以及过程中所结晶出来的普遍概念、 方法和数学理论。只有答案与计算技巧的堆积无法显现数学的妙趣。
　　在《孙子算经》里（共三卷，据推测约成书于西元400年左右）， 下卷的第26题，就是鼎鼎有名的“孙子问题”：

今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？

　　将它翻译成白话：这里有一堆东西，不知道有几个；三个三个去数它们，剩余二个；五个五个去数它们，剩余三个；七个七个去数它们，剩余二个；问这堆东西有几个？精简一点来说：有一个数，用 3 除之余 2；用 5 除之余 3；用 7 除之余 2；试求此数。
　　用现代的记号来表达：假设待求数为 x，则孙子问题就是求解方程式：

⎧⎩⎨⎪⎪x=2　(mod　3)x=3　(mod　5)x=2　(mod　7)

其中 a=b　(mod　n) 表示 a−b 可被 n 整除。
　　这个问题俗称为“韩信点兵”（又叫做“秦王暗点兵”、“鬼谷算”、“隔墙算”、“剪管术”、“神奇妙算”、“大衍求一术”等等），它属于数论 (Number theory) 中的“不定方程问题”(Indeterminate equations)。
孙子给出答案：

答曰：二十三

　　事实上，这是最小的正整数解答。他又说出计算技巧：

术曰：三三数之剩二，置一百四十；五五数之剩三，置六十三；七七之数剩二，置三十。 并之得二百三十三。以二百一十减之，即得。 凡三三数之剩一，则置七十；五五数之剩一，则置二十一；七七数之剩一，则置十五。 一百六以上，以一百五减之，即得。

　　这段话翻译成数学式就是：

x=2×70+3×21+2×15−2×105=140+63+30−210=23

此数是最小的正整数解。
　　为了突显 70、21、15、105 这些数目，明朝的程大位在《算法统宗》（1592年）中，把它们及解答编成歌诀：

三人同行七十稀，五树梅花廿一枝，
七子团圆正半月，除百零五便得知。

　　另外，在宋代已有人编成这样的四句诗：

三岁孩儿七十稀，五留廿一事尤奇，
七度上元重相会，寒食清明便可知。

　　这些都流传很广。“上元”是指正月十五日，即元宵节，暗指“15”；而“寒食”是节令名，从冬至到清明，间隔105日，这段期间叫做“寒食”，故“寒食”暗指“105”。
　　本文我们要来探索韩信点兵问题的各种解法，它们的思路过程与背后所涉及的数学概念和方法。

观察、试误与系统列表

　　按思考的常理，面对一个问题，最先想到的办法就是观察、试误 (trial and error)、投石问路、收集资讯，再经系统化处理，这往往就能够解决一个问题；即使不能解决，对该问题也有了相当的理解，方便于往后的研究或吸收新知。
首先考虑被 3 除之余 2 的问题。正整数可被 3 整除的有 3,6,9,12,，所以被 3 除之余 2 的正整数有 2,5,8,11,14,。其次，被 5 除之余 3 的正整数有 3,8,13,18,。最后，被 7 除之余 2 的正整数有 2,9,16,23,。将其系统地列成表一，以利观察与比较。

表一

　　 我们马上可从表一看出23是最小的正整数解。
　　有一位四年级的小学生，他耐心地继续计算下去，得到第二个答案是128，第三个答案是233，接着又归纳出一条规律从23开始，逐次加105都是答案（这是磨练四则运算的好机会）。从而，他知道孙子问题有无穷多个解答。不过，小学生还没有能力把所有的解答写成一般公式：

x=23+105⋅n,n∈N0　　　　　(1)

其中， N0={0,1,2,3,⋯⋯} 。
　　根据机率论，一只猴子在打字机前随机地打字，终究会打出莎士比亚全集， 其机率为 1。这是试误法中，最令人惊奇的一个例子。人为万物之灵， 使用试误法当然更高明、更有效。总之，我们可以（且必须）从错误中学习。

分析与综合

　　根据笛卡儿（Descartes, 1596～1650）的解题方法论：面对一个难题，尽可能把它分解成许多部分，然后由最简单、最容易下手的地方开始，一步一步地拾级而上，直到原来的难题解决。换言之，你问我一个问题，我就自问更多相关的问题，由简易至复杂，铺成一条探索之路。
现在我们考虑比孙子问题更一般的问题：
问题1. 试求出满足下式之整数 x ：

孙子问题是 r1=2，r2=3，r3=2 的特例：

　　 为了求解这个特例，我们进一步考虑一连串更简单的特例。 基本上，这有两个方向：剩余为 0 或只有单独一个方程式。

单独一个方程式

　　欲求

x=3q1+2　　　　　　　(4)

的整数解x，显然解答的全体为

Ｓ＝｛...,−7,−4,−1,2,5,...｝

这些解答可以写成一个通式：

x=3n+2,n∈Z　　　　　(5)

其中Z表示整数集，事实上，(5)式只是(4)的重述。
进一步，通解公式(5)也可以写成

x=3n+5,n∈Z

或

x=3n+(−4),n∈Z

等等，换言之，通解公式可以表成 x=3n,n∈Z ，与 x=2(或x=−4等等 )这两部分之和。前一部分是 x=3q1 之通解，后一部分是 x=3q1+2 的任何一个解答（叫做特解）。
　　这告诉我们，欲求 x=3q1+2 之通解，可以分成两个简单的步骤： 先求 x=3q1 的通解，再求 x=3q1+2 的任何一个特解，最后将两者加起来就是 x=3q1+2 的通解公式。
　　这对于两个方程式的情形也成立吗？这是否为一般的模式 (pattern)？下述我们将看出，这是肯定的。

两个方程式

　　其次，考虑

{x=3q1+2x=5q2+3　　　　　　(6)

的整数解 x 。为此，我们考虑更简单的齐方程式问题：

{x=3q1+0x=5q2+0　　　　　　(7)

这表示 x 可以同时被 3、5 整除，即 x 是 3、5 的公倍数。因为这两个数互质，所以 3×5=15 是它们的最小公倍数。从而，

x=105⋅n,n∈Z　　　　　　(8)

是(7)式的齐次方程之通解公式。
　　如何求得(6)式的一个特解？这可以采用试误法，也可以系统地来做。今依后者，考虑比(7)式稍微进一步的问题：

{x=3q1+1x=5q2+0　　　　　　　　(9)

这是要在 5 的倍数中

　　　　　　　　　　　　　　

...−10,−5,0,5,10,15...

找被 3 除余 1 者。由于我们只要找一个特解，故不妨选取 x=10 。从而

{x=3q1+1x=5q2+0　　　　　　　　　(10)

的一个特解为 x=2×10 。同理，我们找到

{x=3q1+0x=5q2+1　　　　　　　　　(11)

的一个特解 x=6 ，于是 x=3×6 为

{x=3q1+0x=5q2+3　　　　　　　　　(12)

的一个特解。因此
　　　　　　　　　　

x=2×10+3×6　　　　　　　　(13)

为(6)式的一个特解。
将(8)式与(13)式相加，得到
　　　　　　　

x=2×10+3×6+15⋅n，n∈Z　　(14)

　　这是(6)式的通解公式（穷尽了所有解答）吗？
　　答案是肯定的，我们证明如下：根据上述的建构，显然(14)式为(6)的解答。反过来，设 A 为(6)式的任意解答，则 A−2×10−3×6 为(7)式的解答，而(7) 式的解答形如 15⋅n ，因此 A−2×10−3×6＝15⋅n ，亦即 A 可表成
　　　　　　　

A＝2×10＋3×6＋10⋅n，n∈Z

　　换言之，(6)式的任意解答皆可表成(14)之形，所以(14)式为(6)式之通解公式。

孙子问题

　　现在我们再往前一步，来到孙子问题，即(3)式之求解。仿上述办法，先解齐次方程：

⎧⎩⎨⎪⎪x=3q1+0x=5q2+0x=7q3+0

　　得到通解公式为

x=3×5×7×n=105⋅n，n∈Z　　　　　(15)

　　其次，我们分别找

⎧⎩⎨⎪⎪x=3q1+1x=5q2+0x=7q3+0

⎧⎩⎨⎪⎪x=3q1+0x=5q2+1x=7q3+0

⎧⎩⎨⎪⎪x=3q1+0x=5q2+0x=7q3+1

之特解，得到 x=70,x=21,x=15 。从而

x=2×70+3×21+2×15　　　　　　(16)

为孙子问题（即(3)式）的一个特解。
　　将(15)式与(16)式相加起来，得到

x=2×70+3×21+2×15+105⋅n,n∈Z　　(17)

我们仿上述很容易可以证明，(17)式就是孙子问题的通解公式。 特别地，当 n=−2 时， x=23 为最小正整数解。

更一般的情形

　　最后，我们前进到问题1（即(2)式）之求解。根据上述的解法，我们立即可以写出(2)式的通解公式：

x=70r1+21r2+15r3+105⋅n，n∈Z　　　　　(18)

　　总而言之，对于孙子问题的求解，我们采取了分析与综合的方法：将原问题分解成几个相关的简易问题（相当于物质之分解成原子），分别求得解答后，再将它们综合起来（相当于原子之组合成物质）。这里的综合包括特解的放大某个倍数，相加，然后再加上齐次方程的通解。这非常相像于原子论的研究物质的组成要素、结构、变化和分合之道。

线性结构

　　表象与实体 (appearance and reality) 的关系和互动是哲学的一大主题。通常我们相信，显现在外的表象，背后有规律可循，亦即大自然按机制来出象。
　　准此以观，上述孙子问题的解法，只是技术层面（即表象）而已。我们要再挖深下去，追究潜藏的道理。我们要问：到底背后是什么结构，使得我们的解法可以畅行？
　　为了探究这个问题，让我们对孙子问题作进一步的分析。特别地，我们要转换观点。

问题的转换

　　首先，将(2)式改写成

（19）

图一
　　再将上式看成一个映射 (mapping) 或一部机器 L（如图一）。这部机器的运作 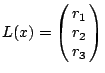， 由(19)式所定义。
　　据此，我们原来的问题就变成：已知产品 要找原料 x，使得。 这是一个典型的解方程式问题。

集合加结构

　　为了要求解这个问题，我们必须研究 L 的性质，以及原料集与产品集的结构。
　　基本上，我们可以说，现代数学就是研究集合加上结构，由此演绎出的所有的结果。这个结构可以是运算的或公理的等等。
　　L 的原料集为整数集

　　在求解孙子问题的过程中，我们用到了两个整数 a、b 的加法 ，以及一个整系数 α 与一个整数 a 的系数乘法 。这两个运算满足一般数系所具有的一些运算律，例如交换律、分配律等等。
　　另一方面，由三个整数所组成的一个向量，例如 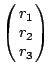，就是 L 的一个产品，而产品集为

　　两个向量的相加，以及系数乘法，分别定义为

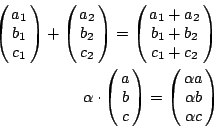
　　但是，最后所得的结果，必须再经过对 3、5、7 的取模操作(modulus operation)，例如

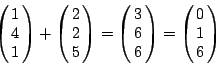
(20)

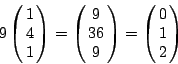
(21)

　　因为这一切都是起源于对 3、5、7 的除法及余数的问题，某数被 3 除，余 0 与余 3 都表示着同一回事，即某数为 3 的倍数。因此利用对 3 同余的观点来看，1+2=0；对 5 同余的观点来看，2+4=1；同理，对 7 同余，那么 4+5=2。

L 的性质

　　现在我们知道，L 是从原料集 Z 到产品集 Z(3,5,7)3 之间的一个映射，记成

　　相对于分合工具的加法与系数乘法，L 具有什么性质呢？解决孙子问题的分析与综合法，如何反映成 L 的性质？
　　我们观察到

而且

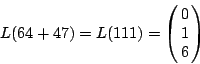
由(20)式知
　

L(64+47)=L(64)+L(47)

同理，易验知

　　一般而言，我们有：
定理1. 映射 满足
(I)

L(x+y)=L(x)+L(y)

(22)

(II）

(23)

其中 x、y、α 皆属于 Z。
　　我们称(21)式为 L 具有加性，(22)式为 L 具有齐性。两者合起来统称为 L 具有叠合原理 (Superposition principle)，或称 L 为一个线性算子 (Linear operator)。 这两条性质是由齐一次函数 f(x)=ax 抽取出来的特征性质。
　　这些似乎有点儿抽象，相当于从算术飞跃到代数的情形。但是，抽象是值得的，它使我们看得更清楚，也易于掌握本质、要点。

线性问题的求解

　　孙子问题就是欲求解线性方程式

L(x)=⎛⎝⎜r1r2r3⎞⎠⎟　　　　　　　(24)

特别地，求解

L(x)=⎛⎝⎜232⎞⎠⎟　　　　　　　(25)

L具有叠合原理（或线性），导致了下列求解线性方程式的三个步骤：

(I)齐次方程

先解齐次方程 L(x)=⎛⎝⎜000⎞⎠⎟ 得到齐次通解 x=105⋅n,n∈Z 。

(II)非齐次方程

其次，解非齐次方程

L(x)=⎛⎝⎜r1r2r3⎞⎠⎟=r1⎛⎝⎜100⎞⎠⎟=r2⎛⎝⎜010⎞⎠⎟=r3⎛⎝⎜001⎞⎠⎟　　　(26)

的一个特解，为此，我们求

L(x)=⎛⎝⎜100⎞⎠⎟,

L(x)=⎛⎝⎜010⎞⎠⎟,

L(x)=⎛⎝⎜010⎞⎠⎟,

之特解，分别得到 x=70,x=21,x=15。 作叠合

x=70r1+21r2+15r3

就是(25)的一个特解。

(III)再作叠合

　　将非齐次方程的一个特解加上齐次通解，得到 x=70r1+21r2+15r3+105⋅n,n∈Z , 就是孙子问题(23式)的通解公式。
　　一般地且抽象地探讨向量空间的性质（一个集合具有加法与系数乘法）、两个向量空间之间的线性算子之内在结构，以及求解相关的线性方程式，这些就构成了线性代数 (Linear Algebra) 的内容。这是从代数学、分析学、几何学、物理学的许多实际解题过程中，抽取出来的一个共通的数学理论架构，不但重要而且美丽。
　　我们也看出，孙子问题是生出线性代数的胚芽之一。这样的问题就是好问题，值得彻底研究清楚。
习题1. 有一堆苹果，七个七个一数剩下三个，十一个十一个一数剩下五个，十三个十三个一数剩下八个，试求苹果的个数，包括最小整数解及通解。

中国剩余定理

　　孙子问题可以再推广，将三个数3、5、7改成两两互质的n个正整数，解法仍然相同。
定理2. 设 m1,m2,…,mn 为 n 个两两互质的正整数，则不定方程式

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x=m1q1+r1x=m2q2+r2　　　⋮　　　　⋮x=mnqn+rn

存在有解答，并且在取模 m1,m2,…,mn 之下，解答是唯一的。复次，(26) 式的通解等于特解加上齐次方程的通解 。
证明： 我们只需证明，当 rk=1,ri=0,∀i≠k 时，(26)式存在有整数解即可。令

Mk=m1m2⋯mk−1mk+1⋯mn

则 Mk 与 mk 互质。由欧氏算则（即辗转相除法）知，存在整数 r,s 使得

rMk+smk=1

有整数解。从而

rMk=−smk+1=1(mod　mk)

故 rMk 即为所求的一个解答。再按线性方程的叠合原理，就可以求得(26)式的通解了。证毕。
注意：当 m1,m2,…,mn 不两两互质时，(26)式可能无解。
习题2. 请读者举出反例。

结语

　　让代数方法行得通的依据，归根究底是数系的运算律，这是代数学的“空气”或“宪法”。同理，让线性方程式的求解行得通的依据是，线性叠合的结构(向量空间的运算律及线性算子的特性),由此发展出线性代数，使我们可以作分析与综合，达到以简御繁的境地。
　　透过各种具体例子的求解过程，逐步锤炼出抽象的数学理论；反过来，数学理论又统合着各种具体问题，让我们看得更清楚；这一来一往的过程是数学发展常见的模式。这种由具体（特殊）生出抽象（普遍），抽象又含纳具体的认识论，值得我们特别留意与欣赏。
　　物理学家费因曼（R.P. Feynman, 1918～1988）批评物理教育说：物理学家老是在传授解题的技巧，而不是从物理的精神层面来启发学生。
这里的“物理”改为“数学”也适用。
　　有没有办法，既学到技巧又掌握精神呢？我们引颈企盼！

---

摘自蔡聪明《谈韩信点兵问题》

---

参考文献：

1. Feynman,R.P.,《Surely You’re Joking,Mr.Feynman, Adventures of a Curious Character》，吴程远中译：《别闹了，费曼先生──科学顽童的故事》。天下文化出版社，1993。
2. Burton, D.M.,《Elementary Number Theory》, Third Edition, Wm. C. Brown Publishers, 1994.
3. Mcleish, J.,《The Story of Numbers, How Mathematics Has Shaped Civilization》, Fawcett,Columbine,N.Y.,1991
4. Janich, K.,《Linear Algebra》, Springer-Verlag, 1994.
5. Katz. V.J. 《A History of Mathematics》, Harper Collins College Publishers, 1993.
6. Martzloff, J.C.,《A History of Chinese Mathematics》, Springer-Verlag, 1997.
7. 林聪源，《数学史──古典篇》，凡异出版社，新竹，1995。
8. 项武义，〈漫谈基础数学的古今中外──从韩信点兵和勾股弦说起〉，《数学传播》第21卷第1期，1997年。
9. 黄武雄，《中西数学简史》，人间文化事业公司，台北，1980年。