dayuhaitang_galaxy

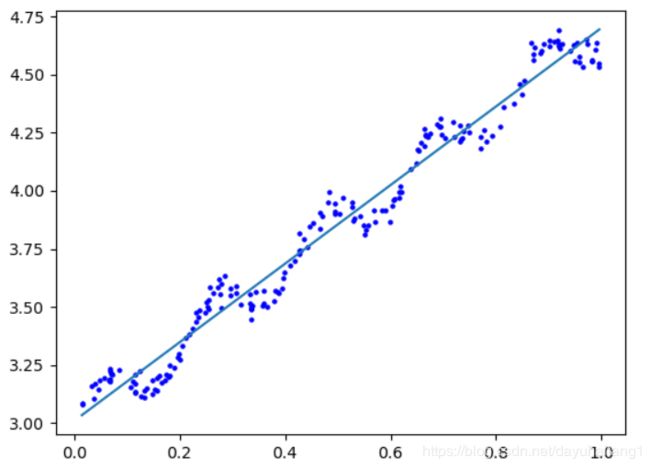
Logistics回归分类

因为自己对回归分类比较好奇，所以就找了找资料做了这篇笔记。

文章目录

一、什么是回归？
二、线性回归

2.1基本形式
2.2回归过程
2.3广义线性模型

三、Logistics回归

3.1模型形式
3.2回归过程

四、代码实现

4.1线性回归
4.2logistics回归

五、小结

一、什么是回归？

这个问题对我来说一直很朦胧，因为虽然之前做过一些回归的实验，但是如果真是让我用语言说出来又不知道说什么，所以就查了查资料。

回归是指研究一组随机变量 $(Y 1 ， Y 2 ， \dots ， Y i)$ 和另一组 $(X 1 ， X 2 ， \dots ， X k)$ 变量之间关系的统计分析方法。(来源于百度)

note：题外话，感觉下面这个故事很有趣，所以也记录一下。Galton(达尔文的表弟)于1877年完成了第一次回归预测，其实验的目的是根据上一代豌豆种子的尺寸来预测下一代豌豆种子的尺寸。在这次实验的过程中他注意到，如果双亲的高度比所有豌豆的平均高度高，那么他们子女的高度则倾向于比平均高度高，但仍不及双亲。因此孩子的高度会出现向着平均高度回退(回归)的现象。这也就是“回归”一词的由来。

那么回归的目的是什么呢？预测数值型的目标值。也就是说我们通过回归分析可以得到一个数学模型，我们可以通过这个模型来预测一些未知的东西。

那么此时就可以更直白的讲，这个数学模型就是所谓的我们经常提到的回归方程，而求解回归方程中的回归系数这个过程就是回归。

二、线性回归

提到回归，不可避免的就要说道一下线性回归，这不仅仅是因为线性回归的形式简单，还因为许多较为复杂的非线性数学模型其实都可以通过线性模型而得到，所以我认为理解线性回归真的很重要。

2.1基本形式

假设给定一个样本 $x={x_1,x_2,x_3...x_n}$ ,则关于该样本的线性模型为：

$f(x)=w^Tx+b$
其中： $w=w_1,w_2....w_n$ 是关于 $x_i$ 的权重系数。

2.2回归过程

本质上来讲，线性回归的过程其实就是确定上面式子中的 $w, b$ 的过程，而问题的关键就是怎样去衡量 $f (x) 与真值 y$ 之间的差距。那么这就涉及到了我们经常会用到的一种指标“均方误差”,并且使均方误差最小化。

$E(D)=argmin_(w,b_)\displaystyle\sum_{i=1}^{m}(f(x_i)-y_i) ^2(单个属性)$
上述公式中没有乘以 $\frac{1}{m}$ ，因为此时它正好对应了“欧式距离”，通过使该模型最小化的方法来求解 $w, b$ 的方法也就是著名的“最小二乘法”。之后就回到了常规套路了，我们对 $E (D)$ 分别对 $w, b$ 进行求导。

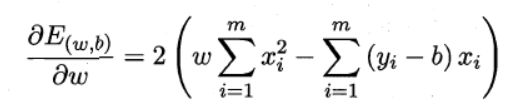
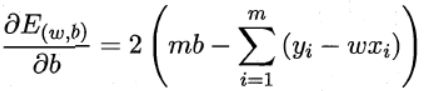
然后令这两个式子都等于0，可以得出下面：

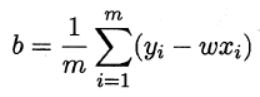
而对于像2.1中多个属性的情况，可以通过向量化来重复上述过程来求取 $w, b$ 。令 $\hat{w}=(w,b)$

则可推导出：

$\hat{w}_{min}=(X^TX)^{-1}X^Ty$

其中 $X^TX)^{-1}$ 是矩阵 $X^TX)$ 的逆矩阵，由此也可以看出这个方程只适用于逆矩阵存在的情况，除此之外就是 $X^TX)$ 很多时候可能不是满秩矩阵，也就是会有多个最优解。

2.3广义线性模型

通过上述的描述，我们可以知晓线性模型形如：
$y=w^Tx+b$
那如果我们感觉样本中的数据所对应的输出 $y$ 应该是在指数尺度上变化的，我们就可以将线性模型修改为：
$Iny=w^Tx+b$
那么此时的 $y 与 x$ 的关系就为非线性函数模型了。我们将其再进行一般化，则
$y=g^{-1}(w^Tx+b)$
其中： $g (.)$ 为单调可微函数，可微也就是连续且足够光滑。

从上述的公式来看，我们确实可以通过使用一种可微函数来把控输出值 $y$ 的意义，由此也就引出了“logistic 回归”。

三、Logistics回归

3.1模型形式

上面讲了那么多的线性模型，但是那些线性模型的目的都是在预测某一数值的目标值，怎么才能使得这些线性模型为我们进行分类呢？这就要使用到“广义线性模型”的概念了。从上可以知道我们可以通过使用一个可微的函数来把控 $y$ 值的输出，考虑到Logistics回归本质上是一个二元分类的任务，所以我们只需要把输出值 $y$ 控制到只有两个结果不就行了。

最为理想的函数当然是“单位阶跃函数”，如下所示：
$y=\begin{aligned} \begin{cases}0,z<0\\ 1/2,z=0\\ 1,z>0 \end{cases} \end{aligned}$
但是“单位阶跃函数”并不连续，所以这个函数也并不理想，因此也就找到了“单位阶跃函数”的替代品“logistic function”(对数几率函数)：
$y=\frac{1}{1+e^{-z}}$
其中：令 $z=w^Tx+b$ 即可满足我们希望 $y$ 值只输出两种结果的需求。

3.2回归过程

同2.2logistics的回归过程仍然是要确定 $w 和 b$ 的值，我们将上述的对数几率函数变化为：
$In\frac{y}{1-y}=w^Tx+b$
如果将式中的 $y$ 视为类后验概率估计 $p (y = 1 ∣ x)$ ,则上面的式子又可以写成：
$In\frac{p(y=1|x)}{p(y=0|x)}=w^Tx+b$
那么有

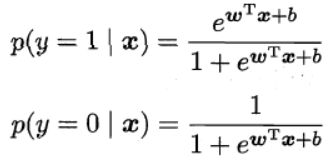
到了这里就需要思考一下了，此时再用“均方误差”最小化来求出参数 $w, b$ 当然是可以的，但是却不建议这么做，这是因为其有可能产生多个最优解(这不利于之后的数值优化方法的使用，如梯度下降法)。为了只产生一个最优解，我们就需要引入另一种方法来求解 $w, b$ 参数了，也是另一种判断模型好坏的标准：极大似然法(MLE)。

在Logistics回归中，极大似然法其实就是在“ $w, b$ ”所有可能的取值中，找到一个能使数据出现的“可能性”最大的那组取值。形式如下所示：

从上面的这个公式(一般式)可以看出，如果每个样本属于其真实标记的概率越大，则模型的性能就越好。这其实很容易理解，举例来说：假如我们使用一个数学模型来对人类的性别进行分类，小明真实的性别是个男孩，如果我们使用我们的模型计算出小明是男孩的概率为99%，那肯定说明我们的模型的性能更好啊；反之，如果模型计算出的概率是19%，则说明模型的性能较差。

同2.2中的过程，令 $\beta=(w,b),\hat{x}=(x,1)，p_1(\hat{x};\beta)=p\{y=1|\hat{x};\beta\},p_0(\hat{x};\beta)=p\{y=0|\hat{x};\beta\}=1-p_1(\hat{x};\beta)$ ,则上面的极大似然公式中的似然项可以写成：

代入原式可得到 $l (w, b)$ 。
$l(w,b)=\sum_{i=1}^mIn(y_ip_1(\hat{x};\beta)+(1-y_i)p_0(\hat{x};\beta))$
最后再令 $l(\beta)=-l(w,b)$ 并且再把 $p (y = 1 ∣ x)$ 和 $p (y = 0 ∣ x)$ 代入进去即得到最终的函数。

此时该函数就是一个关于 $\beta$ 的高阶可导连续凸函数，所以我们可以通过使用一些数值优化方法来求得最优的 $w, b$ 参数，如梯度下降法等。

说了这么多，总结来讲，上述的这个方法其最大的优势就是不需要引入概率模型就可以对分类可能性直接进行建模，这样就可以避免了因为概率模型估计错误而引起后续的一些问题。但是本着学习的态度，我仍然记录了一下引入概率模型应该怎么做。

如果要引入概率模型，那么就需要我们有一定程度的经验知识了，在诸多的数据分布中，有一种描述单个二值随机变量的分布：Bernoulli(伯努利)分布，如下所示：

假设 $y$ 为真值， $\hat{y}$ 为预测值，则Bernoulli概率分布函数如下：
$p(y|x)=\hat{y}^y(1-\hat{y})^{(1-y)}$
那么可得：
$p(y=1|x)=\hat{y};p(y=0|x)=1-\hat{y}$
此时恰好符合我们进行二值分类的条件，那么我们现在只需要使得上述MLE中的 $l (w, b)$ 最大化即可，也就是令下面的函数值最大。
$l(w,b)=\sum_{i-1}^{m}Inp(y_i|x)$
化简一下可以写为：
$l(w,b)=\sum_{i-1}^{m}(y_i*In(\hat{y_i})+(1-y_i)In(1-\hat{y_i}))$

此时这个基于Bernoulli分布而得到的似然函数也是一个连续可导的凸函数，我们仍可以通过使用一些数值优化方法来求得最优的 $w, b$ 参数，如梯度下降法等。

四、代码实现

4.1线性回归

代码如下：

import numpy as np
from tkinter import filedialog
import matplotlib.pyplot as plot

def LoadDataset(fileName):
    """
    加载数据
    :param fileName: 文件名
    :return: 数据集
    """
    file = open(fileName)  # 获取文件对象
    numFeat=len(open(fileName).readline().split('\t'))-1    #读取文件数据属性个数
    X=[];Y=[]       #创建两个数组

    for line in file.readlines():
        lineArr=[]  #创建行数组
        curLine=line.strip().split('\t')       #将每一行的数据按照tab键字符进行分割
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))        #将数据添加到行数组中
        X.append(lineArr)      #将lineArr添加到X中去
        Y.append(float(curLine[-1]))        #记录Y数据

    return X,Y

def StandRegression(xArr,yArr):
    """
    计算回归系数w和b
    :param xArr: x数据
    :param yArr: y数据
    :return: 回归系数
    """
    xMat=np.mat(xArr); yMat=np.mat(yArr).T      #将x与y数据进行矩阵化
    xTx=xMat.T*xMat         #计算x的平方
    if np.linalg.det(xTx)==0.0:     #判断xTx矩阵的行列式的值是否为0
        print("该矩阵为奇异矩阵，无法进行求逆")
        return
    wb=xTx.I*(xMat.T*yMat)
    return wb

#文件对话框获取数据路径
dlg=filedialog.askopenfile(title='打开文件',filetypes=[("文本文件","*.txt"),('Python源文件','*.py')])
fileName=dlg.name       #获取数据文件路径
xArr,yArr=LoadDataset(fileName)     #加载数据
wb=StandRegression(xArr,yArr)   #计算回归系数
print("回归系数：" ,wb)

#绘制数据集散点图和最佳拟合的直线,这一部分类似于MATLAB中的做法
fig=plot.figure()       #获取图形窗口
plot.title='图形窗口'
ax=fig.add_subplot(1,1,1)   #添加一个1行1列，索引为1的子窗口

xMat=np.mat(xArr);      #将xArr变为矩阵，方便下面进行切片
ax.scatter(xMat[:,1].tolist(),yArr,s=5,c="blue")      #绘制散点图

xCopy = xMat.copy()	    #深拷贝xMat矩阵
xCopy.sort(0)		    #排序
yHat=xCopy*wb           #计算出预测的yHat值
ax.plot(xCopy[:,1],yHat)
plot.show()

实现效果：

4.2logistics回归

notice：这里我使用了梯度上升法来求解参数 $w, b$ ,当然我们可能经常听的都是梯度下降法，他们其实是一个意思，你只需要把上面的函数 $l (w, b)$ 变为 $- l (w, b)$ 就可以使用梯度下降法。

梯度上升法的核心思想就是：沿着某一函数的梯度方向来找寻该函数的最大值。也就是使用 $wb=wb+\alpha*\nabla{l(w,b)}$ 等式来循环迭代参数 $w, b$ ，以求出最佳的回归方程。

下面是关于 $\nabla{l(w,b)}$ 简单的推导过程， $l (w, b)$ 我选用了使用Bernoulli分布的似然函数(自我感觉它这个更简单一点*~*)：