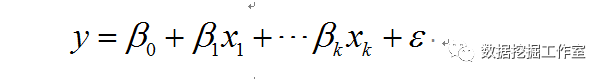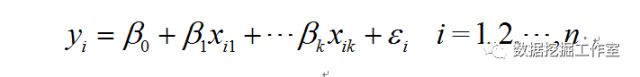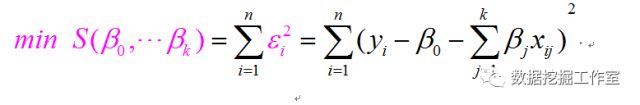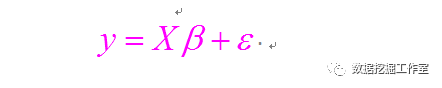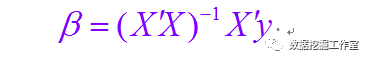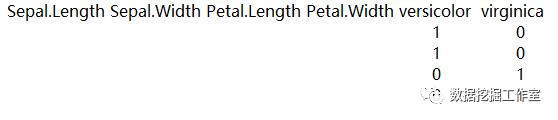多元线性回归、逐步回归、逻辑回归的总结

线性回归，前面用Python从底层一步一个脚印用两种方法实现了回归拟合。在这个高级语言层出不穷的年代，这样做显然不明智，所以我考虑用优秀的数据分析工具——R语言（不敢说最优秀，虽然心里是这么想的，我怕有人要骂我！）做回归分析。包括简单多变量回归、逐步回归、逻辑回归！

对了，上次，用Python写的两篇回归拟合分别是：

多元回归分析，生活中用的很多，因为一个因素可能与很多其它因素有关！言归正传，这里考虑用R语言里面的相关函数做回归分析。

需要的用到的知识储备：

• 线性代数

• 概率论与数理统计

• 高等数学

• R语言基础

下面分别从普通多元线性回归、逐步回归、逻辑回归进行介绍。前面用Python实现的只是一元回归，由于R语言实现线性回归很方便，所以我会着重介绍原理。

多元线性回归

不论是单变量还是多元线性回归分析，他们都是直接或间接（有时候需要通过变量代换）程线性的关系。我们需要找到一个通用的线性模型来描述这种关系，在我们可以接受的误差范围内对数据进行预测或者发现规律。

多元线性回归理论基础

对于一组变量数据，如果我们不管是通过画散点图还是其它方法，知道了一个变量与其它变量程很强线性关系。我们就需要知道，到底是什么样的关系，关系系数是多少。通常是用经典的最小二乘法，因为这样算出的确实是最优的系数，可以保证残差平方和最小的优化目标。

对于一个因变量y，有一组自变量X = (x1,x2,...,xk)，x1,x2,...,xk,eps是列向量，考虑它们之间有如下线性关系：

当然了，这里X = （x1,x2,...,xk）,y都是给的一组数据，就像这样

那么，对每一组（比如第一行）数据，就有如下关系：

目标函数为残差平方和的关于系数beta0,beta1,...,betak的多元二次函数，我们希望找到一组系数使得目标函数值最小，即误差最小。目标函数如下：

学过数学分析或者高等数学的人都知道，这只要关于beta0,beta1,...,betak分别求偏导数，得到k+1方程，再求出零点即可。

我们用矩阵表示各个变量如下：

那么，学过高等代数（数学专业）或者线性代数（工科）都知道，因变量与自变量关系可以表示为：

中间推导过程这里不在赘述了，最终系数向量表达式为：

关于多元线性回归的理论就到这里，有兴趣可以参考：线性回归导论（机械工业出版社 王辰勇 译）

多元线性回归的R语言实现

这里用R语言里面的常用数据集iris来说明，这个数据集包含五个指标，我们这里先只用前面四个：花萼长度、花萼宽度、花瓣长度、花瓣宽度，进行多元线性回归分析。

数据预处理

大家都知道，为了消除不同变量量纲或者数量级不一致，做数据标准化的数据预处理是有必要的。用到的R语言函数是scale()，这个函数的机理具体公式如下：

R语言实现如下：

标准化后数据选择前六行我们看一下：

> head(sl.sc)

     Sepal.Length

[1,]   -0.8976739

[2,]   -1.1392005

[3,]   -1.3807271

[4,]   -1.5014904

[5,]   -1.0184372

[6,]   -0.5353840

下面构建多元线性回归

我们用花萼标准化后的数据sl.sc与其它三个变量做线性回归，先做有常数项的多元回归。

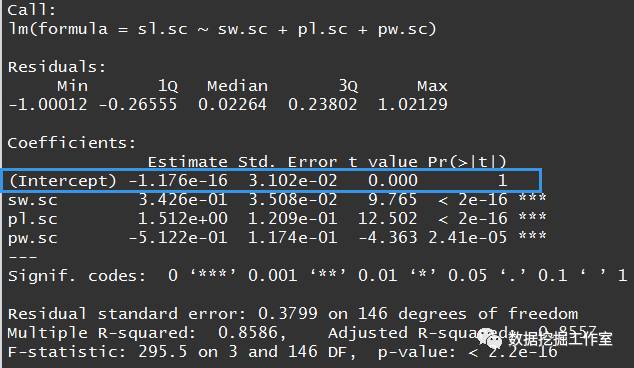
lm.sc <- lm(sl.sc~sw.sc+pl.sc+pw.sc)

summary(lm.sc)

summary(lm.sc)给出了线性回归的相关信息，各个系数Residuals给出了残差的5分位数，Estimate、Std. Error、t value、Pr(>|t|)分别给出了自变量系数、标准误、t值和p值，Multiple R-squared:  0.8586, Adjusted R-squared:  0.8557分别给出了R方与修正的R方，这里 R-squared:  0.8557表示这个线性回归模型可以解释85.57的原数据，还是不错的，后面就不再解释这几个指标的意思了。可以看出无论是每个系数还是总体的p-value都远远小于0.05，给出了三颗星***的等级，但是如图蓝色方框是常数项的值是-1.176e-16，太小了，p值是1，告诉我们常数项可以不用，这些数据是过原点的线性关系。

去掉常数项的多元回归，不同的是，减一表示不要常数项

lm.sc <- lm(sl.sc~sw.sc+pl.sc+pw.sc-1)

summary(lm.sc)

模型详细情况：

显然，去掉后R方，F值没有明显变换，系数等级都是三颗星，表明去掉常数项确实在不影响模型情况下简化了模型。

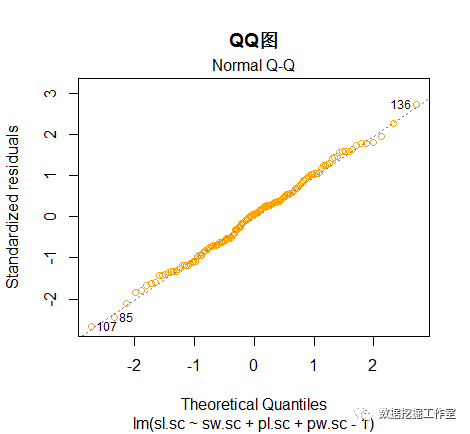
我们来看一下残差图与QQ图：

plot(lm.sc,1,col = 'orange',main = '残差图')

plot(lm.sc,2,col = 'orange',main = 'QQ图')

通过残差图与QQ图也可以明显看出这个不带常数项的线性回归模型是不错的。

逐步回归

逐步回归的基本思想是将变量逐个引入模型，每引入一个解释变量后都要进行F检验，并对已经选入的解释变量逐个进行t检验，当原来引入的解释变量由于后面解释变量的引入变得不再显著时，则将其删除。以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止。以保证最后所得到的解释变量集是最优、最简单的。

逐步回归最常用的挑选准则有修正复相关系数、预测平方和、Cp和AIC等，这里用AIC准则，对于含有P个自变量的回归方程，n为观测值（样本）个数，AIC越小越好，具体计算公式为：

使用R语言构建逐步回归模型

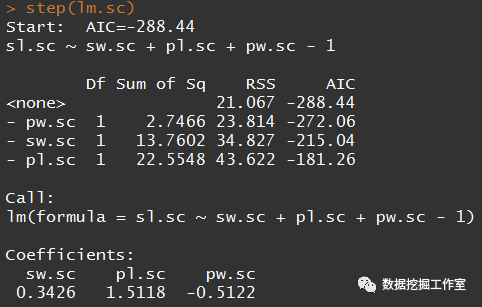
知道原理后，我们试图从三个自变量中筛选出两个，首先看一下上述模型的AIC

step(lm.sc)

显然，三个变量时AIC是最小的，这里为了说明问题，实在要剔除一个变量的话，当然要剔除第一个。因为我们发现剔除pw.sc时AIC为-272.06，如果剔除pl.scAIC就为-181.26，而AIC越小越好，所以就剔除变量pw.sc吧。

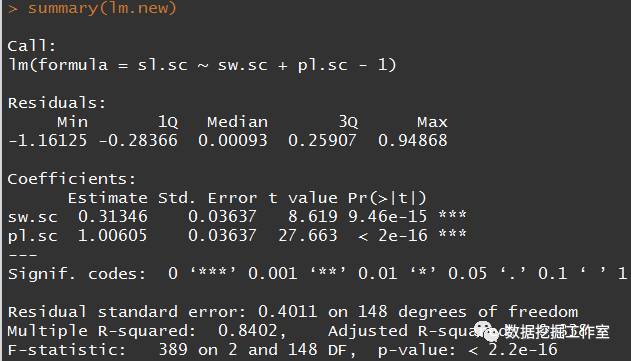
lm.new <- lm(sl.sc~sw.sc+pl.sc-1)

summary(lm.new)

R方稍微减小了一点，因为三个变量AIC最小（即模型最优），提出后肯定会减小的。这里为了说明问题才强行提出一个。

逻辑回归

在介绍逻辑回归前我们先介绍什么是哑变量，其实，R语言用的多的人都知道iris这个数据集有5列，第五列是花的分类：setosa、versicolor、 virginica。那么花萼长度是否与花的分类有关呢？一般是有的。增加三列，我们考虑引入0~1变量，那么对于属于setosa的，记为1，versicolor、 virginica位置记为0，同理就多了3列，这里的0，1就是哑变量。还是为了减少变量，简化模型，我们只增加2列versicolor和 virginica，这样versicolor、 virginica位置都为0时，就属于setosa这个分类，versicolor位置为1时就为versicolor这个分类。0，1是逻辑变量，线性回归引入了逻辑变量，故称为逻辑回归。

下面就进行R语言实现，要不看一下iris数据集长什么样：

第五列变量就有三个水平，都是50条，正好。

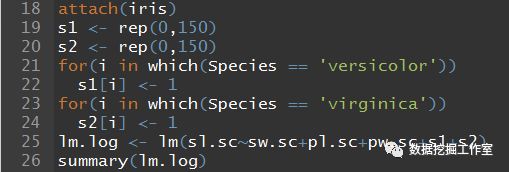
两个for()语句就是构造逻辑变量的，还是很好理解的，这样就有五个变量了。构造的应该像这样：

这里省略了前面的，只为说明构造的逻辑变量（实际应该是s1里面51~100为1，s2里面101~150为1，其它为0）。看一下结果：

所有变量系数p-value都小于0.05，R-squared:  0.8627，比没有增加逻辑变量的R-squared:  0.8557好一些，可见花的分类确实对花萼长度sl.sc有关系。最终表达式为：

猜你可能喜欢