1 损失函数可视化
损失函数一般都是定义在高维度的空间中(比如,在CIFAR-10中一个线性分类器的权重矩阵大小是[10x3073],就有30730个参数),这样要将其可视化就很困难。然而办法还是有的,在1个维度或者2个维度的方向上对高维空间进行切片,就能得到一些直观感受。
例如,随机生成一个权重矩阵\(W\),该矩阵就与高维空间中的一个点对应。然后沿着某个维度方向前进的同时记录损失函数值的变化。
换句话说,就是生成一个随机的方向\(W_{1}\)并且沿着此方向计算损失值,计算方法是根据不同的\(a\)值来计算\(L\left(W+a W_{1}\right)\)。
这个过程将生成一个图表,其x轴是\(a\)值,y轴是损失函数值。同样的方法还可以用在两个维度上,通过改变\(a, b\)来计算损失值\(L\left(W+a W_{1}+b W_{2}\right)\),从而给出二维的图像。在图像中,\(a, b\)可以分别用x和y轴表示,而损失函数的值可以用颜色变化表示。
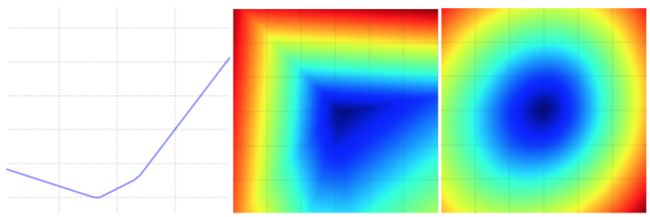
上图是无正则化的多类SVM的损失函数的图示。左边和中间只有一个样本数据,右边是CIFAR-10中的100个数据。
左:a值变化在某个维度方向上对应的的损失值变化。
中和右:两个维度方向上的损失值切片图,蓝色部分是低损失值区域,红色部分是高损失值区域。
2 最优化策略
2.1 随机搜索
既然确认参数集W的好坏蛮简单的,那第一个想到的(差劲)方法,就是可以随机尝试很多不同的权重,然后看其中哪个最好。过程如下:
# 假设X_train的每一列都是一个数据样本(比如3073 x 50000)
# 假设Y_train是数据样本的类别标签(比如一个长50000的一维数组)
# 假设函数L对损失函数进行评价
bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print ('in attempt %d the loss was %f, best %f' % (num, loss, bestloss))
# 输出:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)在上面的代码中,我们尝试了若干随机生成的权重矩阵W,其中某些的损失值较小,而另一些的损失值大些。我们可以把这次随机搜索中找到的最好的权重W取出,然后去跑测试集:
# 假设X_test尺寸是[3073 x 10000], Y_test尺寸是[10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# 找到在每列中评分值最大的索引(即预测的分类)
Yte_predict = np.argmax(scores, axis = 0)
# 以及计算准确率
np.mean(Yte_predict == Yte)
# 返回 0.1555验证集上表现最好的权重W跑测试集的准确率是15.5%,而完全随机猜的准确率是10%,如此看来,这个准确率对于这样一个不经过大脑的策略来说,还算不错嘛!
当然,我们肯定能做得更好些。核心思路是:虽然找到最优的权重\(W\)非常困难,甚至是不可能的(尤其当\(W\)中存的是整个神经网络的权重的时候),但如果问题转化为:对一个权重矩阵集\(W\)取优,使其损失值稍微减少。那么问题的难度就大大降低了。换句话说,我们的方法从一个随机的\(W\)开始,然后对其迭代取优,每次都让它的损失值变得更小一点。
2.2 随机局部搜索
随机局部搜索是每走一步都尝试几个随机方向,如果某个方向是向山下的,就向该方向走一步。这次我们从一个随机\(W\)开始,然后生成一个随机的扰动\(\delta \boldsymbol{W}\)只有当\(W+\delta W\)的损失值变低,我们才会更新。这个过程的具体代码如下:
W = np.random.randn(10, 3073) * 0.001 # 生成随机初始W
bestloss = float("inf")
for i in xrange(1000):
step_size = 0.0001
Wtry = W + np.random.randn(10, 3073) * step_size
loss = L(Xtr_cols, Ytr, Wtry)
if loss < bestloss:
W = Wtry
bestloss = loss
print ('iter %d loss is %f' % (i, bestloss))使用同样的数据(1000),这个方法可以得到21.4%的分类准确率。这个比策略一好,但是依然过于浪费计算资源。
2.3 跟随梯度
前两个策略中,我们是尝试在权重空间中找到一个方向,沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向,因为可以直接计算出最好的方向,这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度(gradient)。
在一维函数中,斜率是函数在某一点的瞬时变化率。梯度是函数的斜率的一般化表达,它不是一个值,而是一个向量。在输入空间中,梯度是各个维度的斜率组成的向量(或者称为导数derivatives)。对一维函数的求导公式如下:
当函数有多个参数的时候,我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量。
3 梯度计算
计算梯度有两种方法:一个是缓慢的近似方法(数值梯度法),但实现相对简单。另一个方法(分析梯度法)计算迅速,结果精确,但是实现时容易出错,且需要使用微分。
3.1 使用有限差值进行数值计算
上节中的公式已经给出数值计算梯度的方法。下面代码是一个输入为函数\(f\)和向量\(x\)计算\(f\)的梯度的通用函数,它返回函数\(f\)在点\(x\)处的梯度:
def eval_numerical_gradient(f, x):
"""
一个f在x处的数值梯度法的简单实现
- f是只有一个参数的函数
- x是计算梯度的点
"""
fx = f(x) # 在原点计算函数值
grad = np.zeros(x.shape)
h = 0.00001
# 对x中所有的索引进行迭代
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
# 计算x+h处的函数值
ix = it.multi_index
old_value = x[ix]
x[ix] = old_value + h # 增加h
fxh = f(x) # 计算f(x + h)
x[ix] = old_value # 存到前一个值中 (非常重要)
# 计算偏导数
grad[ix] = (fxh - fx) / h # 坡度
it.iternext() # 到下个维度
return grad根据上面的梯度公式,代码对所有维度进行迭代,在每个维度上产生一个很小的变化h,通过观察函数值变化,计算函数在该维度上的偏导数。最后,所有的梯度存储在变量grad中。
使用有限差值近似计算梯度比较简单,但缺点在于终究只是近似(因为我们对于h值是选取了一个很小的数值,但真正的梯度定义中h趋向0的极限),且耗费计算资源太多。
3.2 微分计算
微分来分析能得到计算梯度的公式(不是近似),用公式计算梯度速度很快,唯一不好的就是实现的时候容易出错。为了解决这个问题,在实际操作时常常将分析梯度法的结果和数值梯度法的结果作比较,以此来检查其实现的正确性,这个步骤叫做梯度检查。
用SVM的损失函数在某个数据点上的计算来举例:
可以对函数进行微分。比如,对\(w_{y_{i}}\)进行微分得到:
其中1是一个示性函数,如果括号中的条件为真,那么函数值为1,如果为假,则函数值为0。虽然上述公式看起来复杂,但在代码实现的时候比较简单:只需要计算没有满足边界值的分类的数量(因此对损失函数产生了贡献),然后乘以\(x_{i}\)就是梯度了。
注意,这个梯度只是对应正确分类的W的行向量的梯度,那些\(j \neq y_{i}\)行的梯度是:
一旦将梯度的公式微分出来,代码实现公式并用于梯度更新就比较顺畅了。
4 梯度下降
程序重复地计算梯度然后对参数进行更新,这一过程称为梯度下降,他的普通版本是这样的:
# 普通的梯度下降
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # 进行梯度更新上述这个简单的循环在所有的神经网络核心库中都有。
在大规模的应用中(比如ILSVRC挑战赛),训练数据可以达到百万级量级。如果像这样计算整个训练集,来获得仅仅一个参数的更新就太浪费了。
一个常用的方法是计算训练集中的小批量(batches)数据。例如,在目前最高水平的卷积神经网络中,一个典型的小批量包含256个例子,而整个训练集是多少呢?一百二十万个。这个小批量数据就用来实现一个参数更新:
# 普通的小批量数据梯度下降
while True:
data_batch = sample_training_data(data, 256) # 256个数据
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # 参数更新这个方法之所以效果不错,是因为训练集中的数据都是相关的。
要理解这一点,可以想象一个极端情况:在ILSVRC中的120万个图像是1000张不同图片的复制(每个类别1张图片,每张图片有1200张复制)。那么显然计算这1200张复制图像的梯度就应该是一样的。对比120万张图片的数据损失的均值与只计算1000张的子集的数据损失均值时,结果应该是一样的。
实际情况中,数据集肯定不会包含重复图像,那么小批量数据的梯度就是对整个数据集梯度的一个近似。
因此,在实践中通过计算小批量数据的梯度可以实现更快速地收敛,并以此来进行更频繁的参数更新。
小批量数据策略有个极端情况,那就是每个批量中只有1个数据样本,这种策略被称为随机梯度下降(Stochastic Gradient Descent 简称SGD),有时候也被称为在线梯度下降。
这种策略在实际情况中相对少见,因为向量化操作的代码一次计算100个数据 比100次计算1个数据要高效很多。
即使SGD在技术上是指每次使用1个数据来计算梯度,你还是会听到人们使用SGD来指代小批量数据梯度下降(或者用MGD来指代小批量数据梯度下降,而BGD来指代则相对少见)。
小批量数据的大小是一个超参数,但是一般并不需要通过交叉验证来调参。它一般由存储器的限制来决定的,或者干脆设置为同样大小,比如32,64,128等。之所以使用2的指数,是因为在实际中许多向量化操作实现的时候,如果输入数据量是2的倍数,那么运算更快。