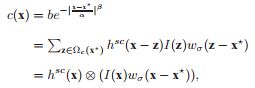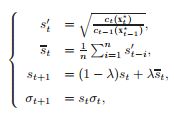论文原文以及Matlab代码下载
算法概述
而STC跟踪算法基于贝叶斯框架,根据跟踪目标与周围区域形成的的时空关系,在图像低阶特征上(如图像灰度和位置)对目标与附近区域进行了统计关系建模。通过计算置信图(confidence map),找到似然概率最大的位置,即为跟踪结果。
算法原理
上下文的重要性
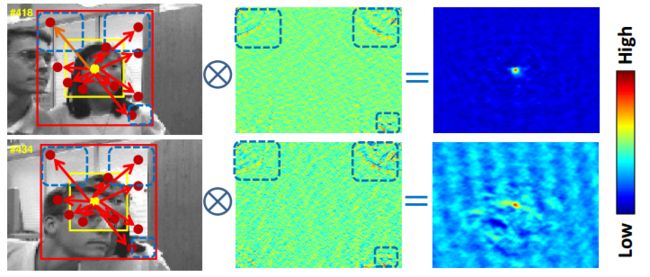
在视觉跟踪,局部上下文包括一个目标和它的附近的一定区域的背景。因为,在连续帧间目标周围的局部场景其实存在着很强的时空关系。例如,上图中的目标存在着严重的阻挡,导致目标的外观发生了很大的变化。然而,因为只有小部分的上下文区域是被阻挡的,整体的上下问区域是保持相似的,所以该目标的局部上下文不会发生很大的变化。因此,当前帧局部上下文会有助于帮助预测下一帧中目标的位置。图中,黄色框的是目标,然后它和它的周围区域,也就是红色框包围的区域,就是该目标的上下文区域。左:虽然出现严重的阻挡导致目标的外观发现很大的变化,但目标中心(由黄色的点表示)和其上下文区域中的周围区域的其他位置(由红色点表示)的空间关系几乎没有发生什么变化。中:学习到的时空上下文模型(蓝色方框内的区域具有相似的值,表示该区域与目标中心具有相似的空间关系)。右:学习到的置信图。
时间信息:邻近帧间目标变化不会很大。位置也不会发生突变。
空间信息:目标和目标周围的背景存在某种特定的关系,当目标的外观发生很大变化时,这种关系可以帮助区分目标和背景。
对目标这两个信息的组合就是时空上下文信息,该论文就是利用这两个信息来进行对阻挡等鲁棒并且快速的跟踪。
置信图定义
在STC算法中,目标的定位问题可用一个目标在预估出现区域各个位置上的出现概率问题来处理。因此如果有一张概率图,可以知道图像中各个位置目标出现的概率,则图像中概率最大的位置就是目标最可能存在的位置,置信图定义为:
$c(x) = P(x|o) = b{e^{ - {{\left| {\frac{{x - {x^*}}}{\alpha }} \right|}^\beta }}}$
$x$表示目标位置,$o$ 表示目标出现, $b$为归一化常量,$\alpha $为尺度参数,$\beta $为形状参数。 ${x^*}$是目标的位置。其中$\beta =1 $能够有效的避免二义性和过拟合。
置信图可分解成为:
置信图似然函数分解为两个概率部分。一个是跟踪目标与周围上下文信息的空间关系的条件概率$P(x,c(z)|o)$,该条件概率使目标与其空间上下文建立关系。当图像中出现多个与目标相似的物体时,STC算法就要依靠空间上下文关系排除非目标本身的其他物体;另一个是目标局部上下文各个点X的上下文先验概率$P(c(z)|o)$。上下文先验概率描述了目标的外观特征。STC算法的核也就在于利用图像中得到的目标外观模型,通过在线学习得到一个时空上下文模型,利用时空上下文模型计算出置信图,从而得到目标最可能存在的位置。
空间上下文模型
定义上一小节中提到的,跟踪目标与周围上下文信息的空间关系的条件概率$P(x,c(z)|o)$ 即是空间上下文模型,定义为:
$P(x,c(z)|o){\rm{ = }}{{\rm{h}}^{{\rm{sc}}}}{\rm{(x - z)}}$
该模型表示目标位置 ${x^*}$与局部区域内点$z$之间的相对距离及方向关系,反映了目标与周围区域的空间关系。由于${h^{sc}}(x - z)$不是一个径向对称函数,因此解决分辨二异性问题。
置信图似然函数分解为两个概率部分。一个是跟踪目标与周围上下文信息的空间关系的条件概率$P(x,c(z)|o)$,该条件概率使目标与其空间上下文建立关系。当图像中出现多个与目标相似的物体时,STC算法就要依靠空间上下文关系排除非目标本身的其他物体;另一个是目标局部上下文各个点X的上下文先验概率$P(c(z)|o)$。上下文先验概率描述了目标的外观特征。STC算法的核也就在于利用图像中得到的目标外观模型,通过在线学习得到一个时空上下文模型,利用时空上下文模型计算出置信图,从而得到目标最可能存在的位置。
空间上下文模型定义
上一小节中提到的,跟踪目标与周围上下文信息的空间关系的条件概率$P(x,c(z)|o)$即是空间上下文模型,定义为:
$P(x,c(z)|o){\rm{ = }}{{\rm{h}}^{{\rm{sc}}}}{\rm{(x - z)}}$
该模型表示目标位置 ${x^*}$与局部区域内点 之间的相对距离及方向关系,反映了目标与周围区域的空间关系。由于${h^{sc}}(x - z)$不是一个径向对称函数,因此解决分辨二异性问题。
上下文先验模型定义
上下文先验概率模型可表示为:
$P(c(z)|o) = I(z){\omega _\sigma }(z - {x^*})$
$I(z)$表示$z$处的灰度值,${\omega _\sigma } = \alpha {e^{ - \frac{{{{\left| z \right|}^2}}}{{{\sigma ^2}}}}}$表示权重函数,该权重函数是由生物视觉系统的focus of attention启发得到的,它表示人看东西的时候,会聚焦在一个确定的图像区域。通常距离目标${x^*}$越近的点对于跟踪目标越重要,因此对应的权重值也越大。而距离越远则越容易被忽视。
时空上下文模型
傅立叶变换得:
$F\left( {b{e^{ - {{\left| {\frac{{x - {x^*}}}{\alpha }} \right|}^\beta }}}} \right) = F({{\rm{h}}^{{\rm{sc}}}}(x)) \odot F(I(x){\omega _\sigma }(x - {x^*}))$
所以:
${{\rm{h}}^{{\rm{sc}}}}(x) = {F^{ - 1}}\left( {\frac{{F\left( {b{e^{ - {{\left| {\frac{{x - {x^*}}}{\alpha }} \right|}^\beta }}}} \right)}}{{F(I(x){\omega _\sigma }(x - {x^*})}}} \right)$
第t+1帧的时空上下文模型$H_{t + 1}^{stc}(x)$的更新公式为:
$H_{t + 1}^{stc}(x) = (1 - \rho )H_t^{stc} + \rho h_t^{sc}$
$\rho $为模型学习速率。这样算法通过不断学习到的空间上下文模型结合前一倾的时空上下文模型,就得到了当前顿的时空上下文模型,再利用该模型更新置信图,从而计算出当前顿目标的位置。
跟踪
得到时空上下文模型后,我们就可以在新的一帧计算目标的置信图了:
${c_{t + 1}}(x) = {F^{ - 1}}(H_{t + 1}^{stc}(x) \odot {I_{t + 1}}(x){\omega _{\sigma t}}(x - {x_t}*))$
然后置信图中值最大的位置,就是我们的目标位置了:
$x_{_{t + 1}}^* = \mathop {\arg \max }\limits_{x \in \Omega c(x_t^*)} {c_{t + 1}}(x)$
尺度更新
${\omega _\sigma } = \alpha {e^{ - \frac{{{{\left| z \right|}^2}}}{{{\sigma ^2}}}}}$中的$\sigma $应随着时间变化进行更新,更新的方法是:
算法步骤
t帧:在该帧目标(第一帧由人工指定)已经知道的情况下,我们计算得到一个目标的置信图(Confidence Map,也就是目标的似然)。通过生物视觉系统上的focus of attention特性我们可以得到另一张概率图(先验概率)。通过对这两个概率图的傅里叶变换做除再反傅里叶变换,就可以得到建模目标和周围背景的空间相关性的空间上下文模型(条件概率)。然后我们用这个模型去更新跟踪下一帧需要的时空上下文模型。
t+1帧:利用t帧的上下文信息(时空上下文模型),卷积图像得到一个目标的置信图,值最大的位置就是我们的目标所在地。或者理解为图像各个地方对该上下文信息的响应,响应最大的地方自然就是满足这个上下文的地方,也就是目标了。
Ref:
时空上下文视觉跟踪(STC)算法的解读与代码复现