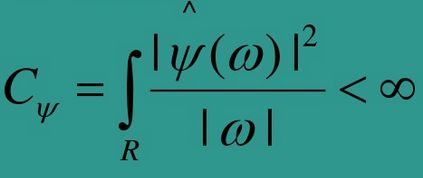MATLAB中的连续小波变换CWT
下面来介绍一下如何在MATLAB实现CWT,也就是我们常说的连续小波变换,具体如下:
所谓小波(wavelet),即存在于一个较小区域的波。小波函数的数学定义是:设ψ(t)为一平方可积函数,即ψ(t)∈L2(R),若其傅里叶变换Ψ(ω)满足条件:
则称ψ(t)为一个基本小波或小波母函数,并称上式是小波函数的可允许条件。
1、打开MATLAB,在其主界面的编辑器中写入下列代码:
clear; %清除MATLAB工作环境中现有的变量
load wbarb; %装入图像
subplot(2,2,1);image(X);colormap(map);
title('原始图像');
disp('原始图像X的大小:');
whos('X');
%对图像用bior3.7小波进行二层小波分解
[c,s]=wavedec2(X,2,'bior3.7');
%提取小波分解结构中第一层的低频系数和高频系数
ca1=appcoef2(c,s,'bior3.7',1);
ch1=detcoef2('h',c,s,1);
cv1=detcoef2('v',c,s,1);
cd1=detcoef2('d',c,s,1);
%分别对各频率成分进行重构
a1=wrcoef2('a',c,s,'bior3.7',1);
h1=wrcoef2('h',c,s,'bior3.7',1);
v1=wrcoef2('v',c,s,'bior3.7',1);
d1=wrcoef2('d',c,s,'bior3.7',1);
c1=[a1,h1;v1,d1];
%显示分解后各频率分量的信息
subplot(2,2,2);image(c1);
axis square;
title('分解后低频和高频信息');
%下面进行图像压缩处理
%保留小波分解第一层低频信息,进行图像的压缩
%第一层的低频信息即ca1,显示第一层的低频信息
%首先对第一层信息进行量化编码
ca1=appcoef2(c,s,'bior3.7',1);
ca1=wcodemat(ca1,440,'mat',0);
%改变图像的高度
ca1=0.5*ca1;
subplot(2,2,3);image(ca1);colormap(map);
axis square;
title('第一次压缩图像');
disp('第一次压缩图像的大小:');
whos('ca1');
% 保留小波分析分解第二层低频信息,进行图像的压缩,此时压缩比更大
% 第二层的低频信息ca2,显示第二层的低频信息
ca2=appcoef2(c,s,'bior3.7',2);
ca2=wcodemat(ca2,440,'mat',0);
ca2=0.25*ca2;
subplot(2,2,4);image(ca2);colormap(map);
axis square;
title('第二次压缩图像');
disp('第二次压缩图像的大小:');
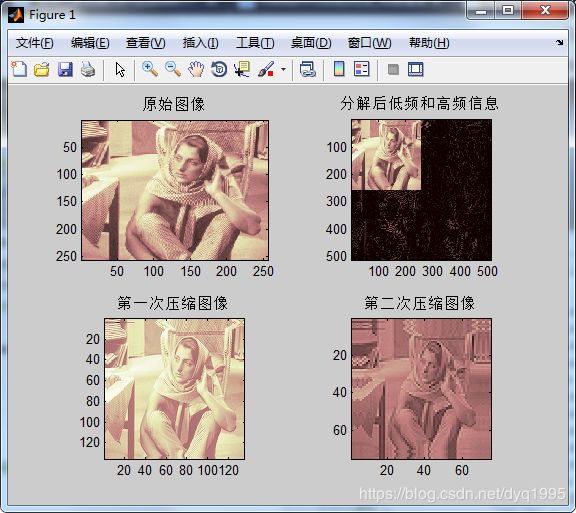
whos('ca2');2、代码保存至自定义路径下,点击运行,结果如下:
如图所示,通过CWT变换后,压缩图像的大小一次比一次减少,并且所占的位数也随之减小,分解的低高频信息是非均匀化的,可以看出连续小波基函数的一个重要性质是窗口面积不随参数a、τ而变,它是小波母函数的时、频窗口宽度Δt和Δω的积。至此基本介绍完毕,请大家继续关注!!!