频域处理：傅里叶变换及小波变换

引言

图像处理–>频域处理–>傅里叶变换、小波变换。用另一种方法来观察世界的话，你会发现世界是永恒不变的。

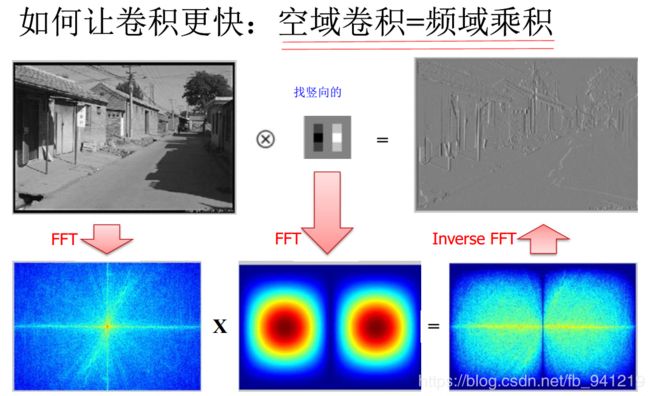
1、傅里叶变换

傅里叶变换

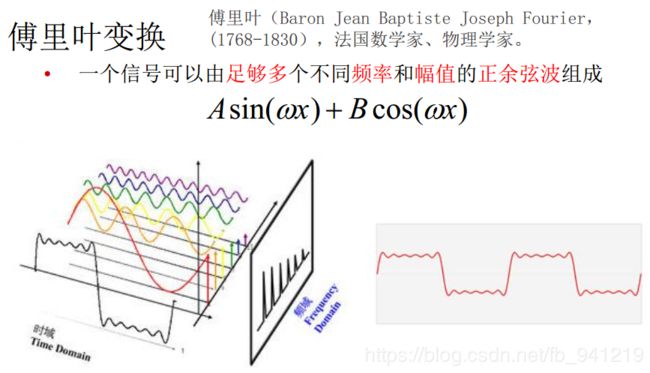
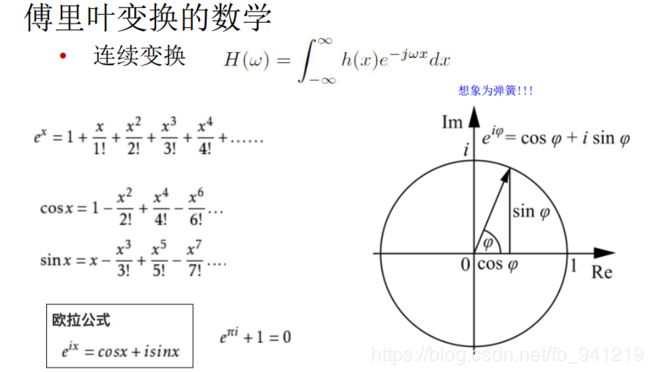
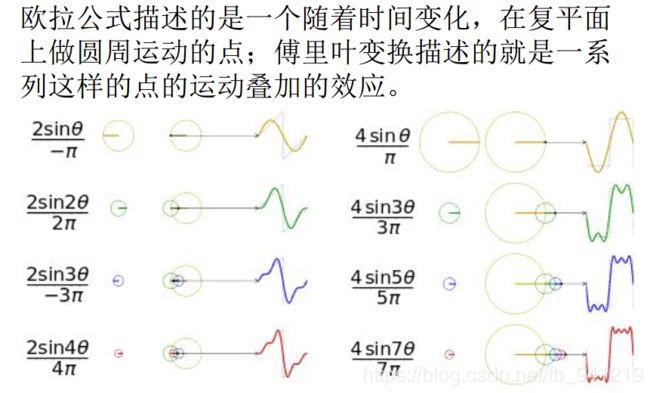
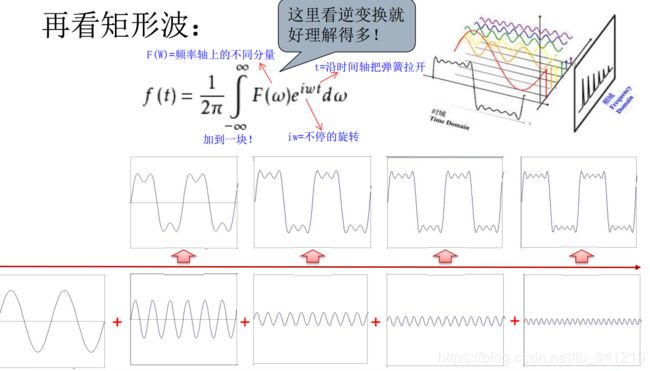
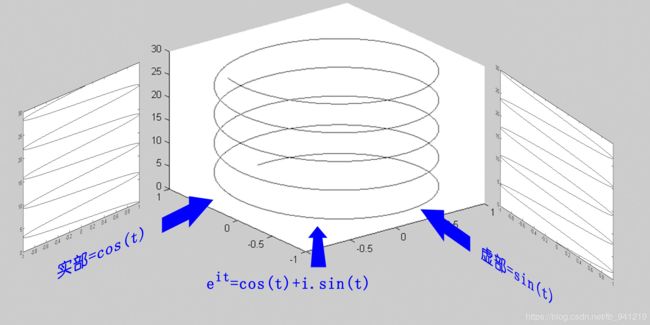
欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
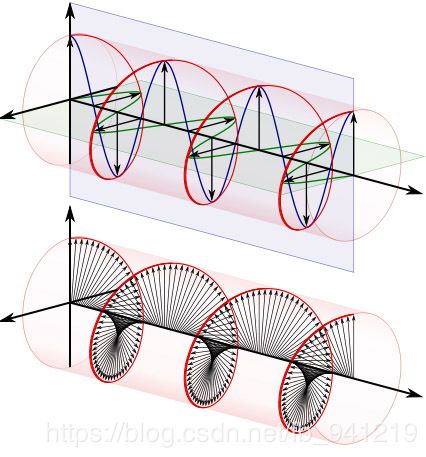
由欧拉公式知道：正弦波的叠加，也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加：

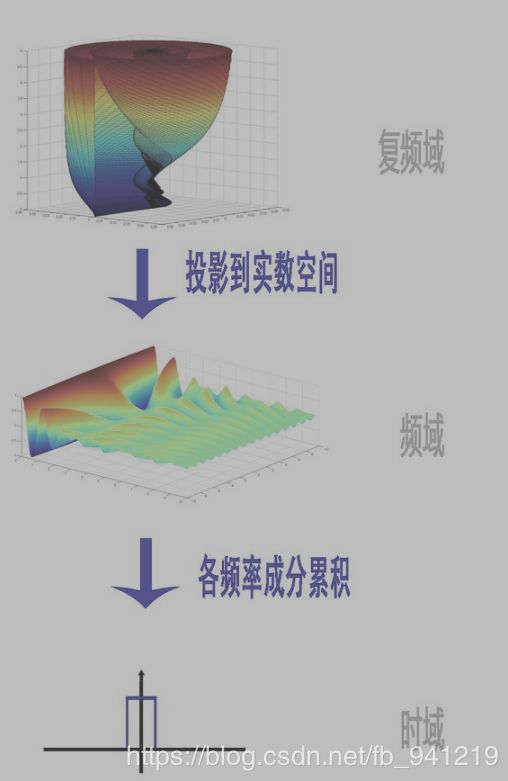
复数就是一个能把平面进行均匀缩放和旋转的乘子。
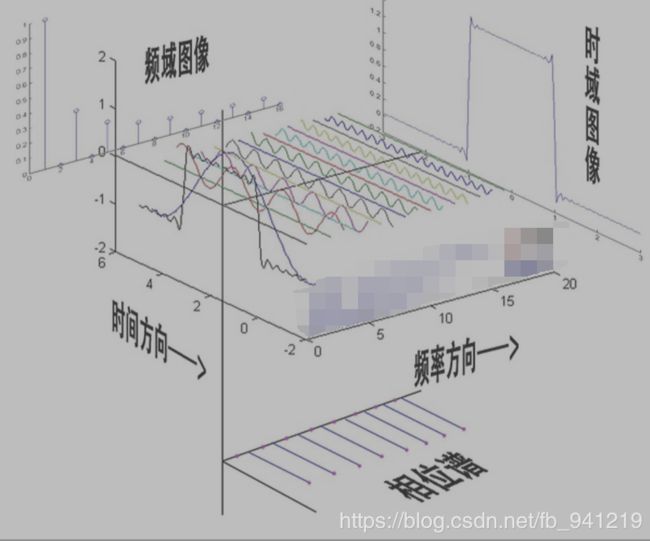
通过时域到频域的变换，得到了一个从侧面看的频谱，但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少，而没有提到相位。基础的正弦波A.sin(wt+θ)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱（振幅谱）是不够的，还需要一个相位谱。
纠正一个概念：时间差并不是相位差。如果将全部周期看作2Pi或者360度的话，相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi，就得到了相位差。
在完整的立体图中，将投影得到的时间差依次除以所在频率的周期，就得到了最下面的相位谱。所以，频谱是从侧面看，相位谱是从下面看。

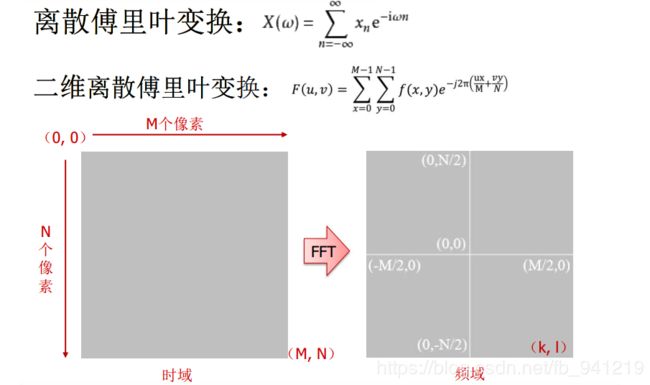
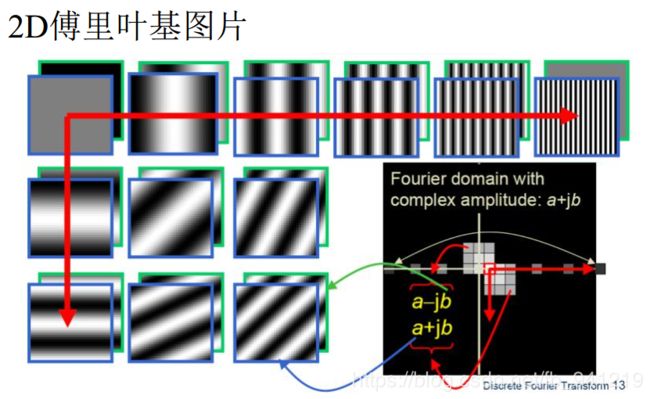
$$频率内低外高,图二只留下中间部分也就是中间部分也就是主体部分，细节部分去除；高通相反。$$

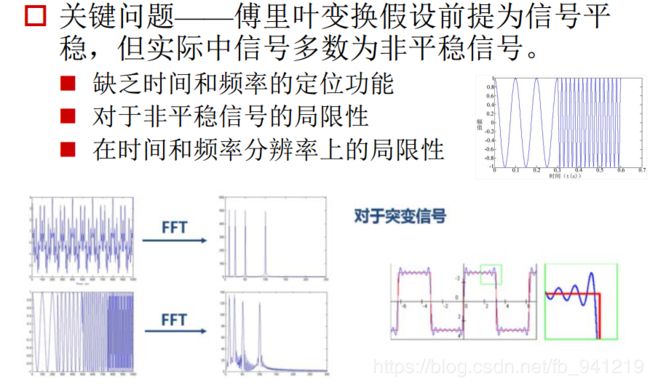
短时傅立叶变换（Short-time Fourier Transform,STFT）也叫加窗傅立叶变换，顾名思义，就是因为傅立叶变换的时域太长了，所以要弄短一点，这样就有了局部性。
定义：把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，再傅里叶变换，就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。
时域上分成一段一段做FFT，就可以知道频率成分随着时间的变化情况。

$$时频图$$

2、小波变换

小波变换
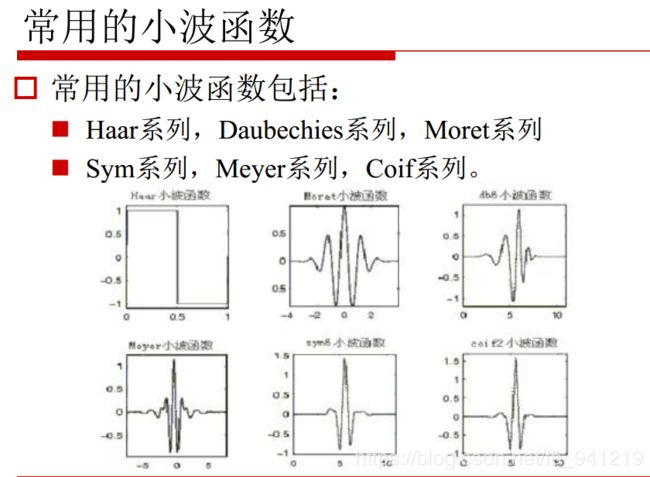
对于加窗傅立叶变换让人头疼的就是窗口的大小问题，如果让窗口的大小可以改变，就完美了。小波就是基于这个思路，但是不同的是。STFT是给信号加窗，分段做FFT；而小波变换并没有采用窗的思想，更没有做傅里叶变换。小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间。即是做傅里叶变换只能得到一个频谱，做小波变换却可以得到一个时频谱。

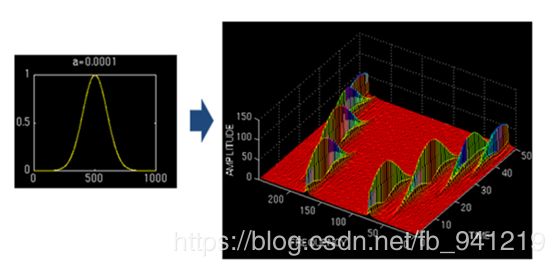
从公式可以看出，不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，平移量 τ控制小波函数的平移。尺度就对应于频率（反比），平移量 τ就对应于时间。

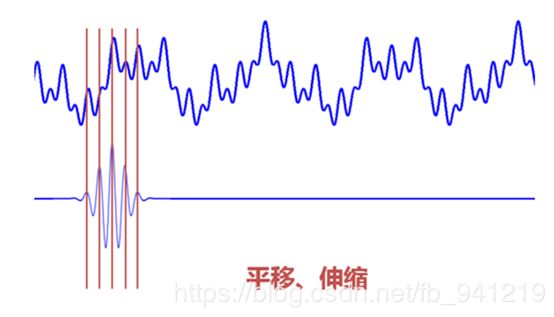
当伸缩、平移到这么一种重合情况时，也会相乘得到一个大的值。这时候和傅里叶变换不同的是，这不仅可以知道信号有这样频率的成分，而且知道它在时域上存在的具体位置。而当每个尺度下都平移着和信号乘过一遍后，就知道信号在每个位置都包含哪些频率成分，就可以对非稳定信号做时频分析。

3、程序

fft:

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('./opencv.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

opencv+dft

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main()
{
    Mat I = imread("lena.jpg", IMREAD_GRAYSCALE);       //读入图像灰度图

    //判断图像是否加载成功
    if (I.empty())
    {
        cout << "图像加载失败!" << endl;
        return -1;
    }
    else
        cout << "图像加载成功!" << endl << endl;

    Mat padded;                 //以0填充输入图像矩阵
    int m = getOptimalDFTSize(I.rows);
    int n = getOptimalDFTSize(I.cols);

    //填充输入图像I，输入矩阵为padded，上方和左方不做填充处理
    copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));

    Mat planes[] = { Mat_(padded), Mat::zeros(padded.size(),CV_32F) };
    Mat complexI;
    merge(planes, 2, complexI);     //将planes融合合并成一个多通道数组complexI

    dft(complexI, complexI);        //进行傅里叶变换

    //计算幅值，转换到对数尺度(logarithmic scale)
    //=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
    split(complexI, planes);        //planes[0] = Re(DFT(I),planes[1] = Im(DFT(I))
                                    //即planes[0]为实部,planes[1]为虚部
    magnitude(planes[0], planes[1], planes[0]);     //planes[0] = magnitude
    Mat magI = planes[0];

    magI += Scalar::all(1);
    log(magI, magI);                //转换到对数尺度(logarithmic scale)

    //如果有奇数行或列，则对频谱进行裁剪
    magI = magI(Rect(0, 0, magI.cols&-2, magI.rows&-2));

    //重新排列傅里叶图像中的象限，使得原点位于图像中心
    int cx = magI.cols / 2;
    int cy = magI.rows / 2;

    Mat q0(magI, Rect(0, 0, cx, cy));       //左上角图像划定ROI区域
    Mat q1(magI, Rect(cx, 0, cx, cy));      //右上角图像
    Mat q2(magI, Rect(0, cy, cx, cy));      //左下角图像
    Mat q3(magI, Rect(cx, cy, cx, cy));     //右下角图像

    //变换左上角和右下角象限
    Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    //变换右上角和左下角象限
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);

    //归一化处理，用0-1之间的浮点数将矩阵变换为可视的图像格式
    normalize(magI, magI, 0, 1, CV_MINMAX);

    imshow("输入图像", I);
    imshow("频谱图", magI);
    waitKey(0);


    return 0;
}

小波 变换.