降维算法原理篇:主成分分析PCA、奇异值分解SVD、因子分析法FA、独立成分分析ICA等原理详推
一、前话
二、主成分分析法PCA
三、奇异值分解SVD
四、因子分析法FA
五、独立成分分析ICA
六、缺失值比率
七、低方差滤波
八、高相关滤波
创作不易,如需转载,请注明出处,谢谢!
一、前话
在降维算法中,我们经常要用到协方差的概念,下面给出协方差,相关系数等概念解释
协方差描述两个变量的相关程度,同向变化时协方差为正,反向变化时协方差为负,而相关系数也是描述两个变量的相关程度,只是相关系数对结果相当于做了归一化处理,协方差的值范围是负无穷到正无穷,而相关系数值范围是在负一到正一之间,详细描述参考:如何通俗易懂地解释「协方差」与「相关系数」的概念
数据降维作用1、减少存储空间
2、低维数据减少模型训练用时
3、一些算法在高维表现不佳,降维提高算法可用性
4、删除冗余数据
5、有助于数据的可视化
二、 主成分分析法PCA
1、PCA主成分分析法思想
方差的大小描述一个变量的信息量,对于模型来说方差越小越稳定,但是对于数据来说,我们自然是希望数据的方差大,方差越大表示数据越丰富,维度越多
方差大的方向是信号的方向,方差小的方向是噪声的方向,我们在数据挖掘模型处理中,往往需要提高信噪比,即是信号和噪声的比例,因此相对于下图既是保留signal方向的数据,对noise方向的数据进行缩减,达到对原始数据一个不错的近似
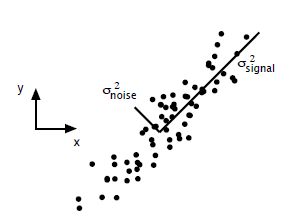
当进行数据降维的时候,我们一般都是对列进行压缩,即对数据的特征进行压缩,当然我们也可以对数据行进行压缩,即将相似的数据合并
PCA本质上是将方差最大的方向作为第一维特征,方差描述的是数据的离散程度,方差最大的方向即是能最大程度上保留数据的各种特征,接下来第二维特征既选择与第一维特征正交的特征,第三维特征既是和第一维和第二维正交的特征
PCA的思想是将N维特征映射到K维上(K
2、PCA算法的主要步骤
设现在有n条d维的数据,d表示数据特征数
(1) 将原始数据按列组成n行d列矩阵X
(2) 将X的每一列进行零均值化,即将这一列的数据都减去这一列的均值,目的:防止因为某一维特征数据过大对协方差矩阵的计算有较大的影响
(3) 求出2中零均值化后矩阵的协方差矩阵
C = 1 m X T X C = \ \frac{1}{m}X^{T}X C= m1XTX
(4) 求出协方差矩阵的特征值和对应的特征向量
(5) 将特征向量按照对应的特征值大小从大到小排列成矩阵,取前k行组成矩阵P,而选择的k特征个数可以利用对前K个大的特征值求和来判断占了整个特征值和的比例来看对原始数据特征保留的程度
(6) Y = XP 即是降维到k为维后的数据
3、PCA理论推导
PCA即将一个高维数据映射到低维,假设映射前的m个n维数据为:
x i = ( x 1 i , x 2 i , … , x m i ) x^{i} = \ \left( x_{1}^{i},\ x_{2}^{i},\ldots,x_{m}^{i} \right) xi= (x1i, x2i,…,xmi)
若我们已经成功选择了k个重要的特征构建降维后空间的k个标准正交基,假设W是标准正交基构成的矩阵,k个正交基
W = [ w 1 , w 2 , … , w k ] W = \lbrack w_{1},\ w_{2},\ldots,\ w_{k}\rbrack W=[w1, w2,…, wk]
假设映射后空间的数据为:
z i = ( z 1 i , z 2 i , … , z k i ) z^{i} = \ (z_{1}^{i},z_{2}^{i},\ldots,z_{k}^{i}) zi= (z1i,z2i,…,zki)
则在PCA中我们主要是寻找重要的前k个特征构成标准正交基,这样便可将高维降维:
z i = W x i z^{i} = \ Wx^{i} zi= Wxi
接下来我们看如何求解W,看W和原数据x的关系,拿到原数据后,第一步需要对数据做零均值归一化处理,因此原数据的均值为0
∑ i = 1 m x i = 0 \sum_{i = 1}^{m}x^{i} = 0 i=1∑mxi=0
则数据xi、xj的协方差矩阵为:
Σ ij = = c o n ( x i , x j ) = E [ ( x i − E ( x i ) ) ( x j − E ( x j ) ) ] \Sigma_{\text{ij}} = \ = \ con\left( x^{i},\ x^{j} \right) = E\lbrack(x^{i} - E(x^{i}))(x^{j} - E(x^{j}))\rbrack Σij= = con(xi, xj)=E[(xi−E(xi))(xj−E(xj))]
E(x)=0, 因此原数据的协方差矩阵为:
Σ = 1 m ∑ i = 1 m x ( i ) x ( i ) T ) = 1 m X X T \Sigma = \ \frac{1}{m}\sum_{i = 1}^{m}{x^{(i)}x^{{(i)}^{T}}}) = \ \frac{1}{m}XX^{T} Σ= m1i=1∑mx(i)x(i)T)= m1XXT
下面通过推导证明W中选的k个重要特征是样本数据的协方差矩阵 XXT 的前k个重要的特征向量组成的,设λ是特征值,即证明有下式成立:
X X T W = λ W XX^{T}W = \ \lambda W XXTW= λW
下面利用样本点到降维超平面的距离足够近来推导降维空间特征向量W与原始样本点数据协方差的特征向量之间的关系,第一步利用zi和W恢复数据为:
x i ‾ = W z i \overset{\overline{}}{x^{i}} = Wz^{i} xi=Wzi
最小化样本点到降维超平面的距离:
min ∑ i = 1 m ∣ ∣ x i ‾ − x i ∣ ∣ \min\sum_{i = 1}^{m}{||\overset{\overline{}}{x^{i}} - \ x^{i}||} mini=1∑m∣∣xi− xi∣∣
下面给出对于上式的推导公式

上式中加号后半项是常数,因此可以将上式等价于:
arg − t r ( W T X X T W ) s.t. W T W = I \arg\operatorname{}{- tr(W^{T}XX^{T}W)}\text{\ \ \ \ s.t.\ }W^{T}W = I arg−tr(WTXXTW) s.t. WTW=I
利用拉格朗日乘子法得到:
J ( W ) = − t r ( W T X X T W ) + λ ( W T W − I ) J\left( W \right) = - tr\left( W^{T}XX^{T}W \right) + \lambda(W^{T}W - I) J(W)=−tr(WTXXTW)+λ(WTW−I)
对W求导整理得:
X X T W = λ W XX^{T}W = \ \lambda W XXTW= λW
4、PCA之最大方差思想证明
最大方差理论阐述:方差最大的方向是保留数据特征最多的方向,也即是特征值最大的方向
样本点在超平面上的投影能尽可能的分开,即投影后数据的方差尽可能大,保留原始数据特征尽可能最多,下面证明我们选取的W中k个特征方向也是最大方差方向,下面公式中的u既是3pca理论推导中的W,都是选取的重要的特征方向

数据样本是xi,主成分方向为u,u是直线的斜率也是直线的方向向量,设定为单位向量,将数据xi投影到主成分方向u上,使得投影后的样本方差最大,样本数据都做了零均值归一化处理,因此数据在投影后的均值为0,数据在投影后的方差为:
1 m ∑ i = 1 m ( x ( i ) T u ) 2 = 1 m ∑ i = 1 m u T x ( i ) x ( i ) T u = u T ( 1 m ∑ i = 1 m x ( i ) x ( i ) T ) u \frac{1}{m}\sum_{i = 1}^{m}{(x^{{(i)}^{T}}u)}^{2} = \ \frac{1}{m}\sum_{i = 1}^{m}{u^{T}x^{(i)}x^{{(i)}^{T}}u} = \ u^{T}(\frac{1}{m}\sum_{i = 1}^{m}{x^{(i)}x^{{(i)}^{T}}})u m1i=1∑m(x(i)Tu)2= m1i=1∑muTx(i)x(i)Tu= uT(m1i=1∑mx(i)x(i)T)u
等式右边括号中既是样本特征的协方差矩阵,因此我们令:
Σ = 1 m ∑ i = 1 m x ( i ) x ( i ) T ) \Sigma = \ \frac{1}{m}\sum_{i = 1}^{m}{x^{(i)}x^{{(i)}^{T}}}) Σ= m1i=1∑mx(i)x(i)T)
另外我们令方差为λ:
λ = 1 m ∑ i = 1 m ( x ( i ) T u ) 2 \lambda = \ \frac{1}{m}\sum_{i = 1}^{m}{(x^{{(i)}^{T}}u)}^{2} λ= m1i=1∑m(x(i)Tu)2
这样方差的表达式写成如下形式,其中u是单位向量:
λ = u T Σ u \lambda = \ u^{T}\Sigma u λ= uTΣu
u λ = u u T Σ u = Σ u = λ u u\lambda = \ uu^{T}\Sigma u = \ \Sigma u = \ \lambda u uλ= uuTΣu= Σu= λu
Σ是协方差矩阵,λ表示Σ的特征值,u是特征向量,并且我们上面令得方差为λ,因此从这里我们便可以得出,数据方差最大的方向既是数据协方差矩阵对应的特征值最大的方向,因此我们只需要对特征值进行特征值分解,然后去前k个最大的特征值对应的特征向量,既是最佳的k维新特征,且k维新特征是相互正交的
5、Kernel PCA
对非线性数据做降维处理,下面首先给出一张PCA和kernel PCA的实例图:

PCA不仅可以从协方差矩阵C入手,也可以从kernel maxtrix K入手,Kernel Pca的思路:
(1) 利用 kernel tricks 计算 kernel matrix K
(2) 对K做SVD分解,找到topk的特征向量
(3) 把高维数据 x 投射到 k 个特征向量上,从而把它降低到 k 维
按照PCA的思路,我们要对协方差矩阵C=XTX做SVD分解,并且C的维度将会是m*m,但是Kernel PCA的思路却是对Kernel Matrix K做SVD分解,如果是线性kernel的话,K =XXT 维度是n*n,下面给出Kernel PCA和PCA的关系推导:

其中将矩阵U用X的线性来表示,有:U = αX,因此将X映射到低维空间:
U X T = α X X T = α K UX^{T} = \ \alpha XX^{T} = \ \alpha K UXT= αXXT= αK
下图展示了传统PCA的投影和Kernel PCA的投影效果比较:

三、奇异值分解SVD
SVD可以看成是对PCA主特征向量的一种解法,在上述PCA介绍过程中,为了求数据X的主特征方向,我们通过求协方差矩阵 XXT 的特征向量来表示样本数据X的主特征向量,但其实我们可以通过对X进行奇异值分解得到主特征方向,下面我们首先比较一下特征值分解和奇异值分解,然后分析一下特征值和奇异值的关系以及SVD在PCA中的应用
1、特征值分解
特征值分解,特征值分解的矩阵必须是方阵,特征值分解的目的:提取这个矩阵最重要的特征,特征值表示这个特征有多重要,特征向量即表示这个特征是什么,可以理解是这个变化最主要的方向
A v = λ v Av = \ \lambda v Av= λv
A = Q Σ Q − 1 A = Q\Sigma Q^{- 1} A=QΣQ−1
对方阵A进行特征值分解,则Q是由A的特征向量构成的矩阵,Q中的矩阵都是正交的,Σ是对角阵,对角线上的元素既是方阵A的特征值
2、SVD 奇异值分解
特征值分解只能够对于方阵提取重要特征,奇异值分解可以对于任意矩阵
A m ∗ n = U m ∗ m Σ m ∗ n V n ∗ n T A_{m*n} = \ U_{m*m}\Sigma_{m*n}V_{n*n}^{T} Am∗n= Um∗mΣm∗nVn∗nT
U是左奇异矩阵,V是右奇异矩阵,均是正交矩阵,Σ是对角阵,除对角线元素外都是0,对角线元素是奇异值,在大多数情况下,前10%甚至前1%的奇异值的和便占据了全部奇异值之和的99%以上了,因此当利用奇异值分解对数据进行压缩时,我们可以用前r个大的奇异值来近似描述矩阵:
A m ∗ n = U m ∗ r Σ r ∗ r V r ∗ n T A_{m*n} = \ U_{m*r}\Sigma_{r*r}V_{r*n}^{T} Am∗n= Um∗rΣr∗rVr∗nT
3、奇异值分解和特征值分解关联
首先我们写出ATA的特征值分解式如下:
( A T A ) v i = λ v i \left( A^{T}A \right)v_{i} = \ \lambda v_{i} (ATA)vi= λvi
其中v向量既是奇异值分解公式中向量v,假设σ是奇异值,奇异值是特征值取平方根,则:
σ i = λ i \sigma_{i} = \ \sqrt{\lambda_{i}} σi= λi
σ i = A v i / u i \sigma_{i} = Av_{i}/u_{i} σi=Avi/ui
u i = 1 σ i A v i u_{i} = \ \frac{1}{\sigma_{i}}Av_{i} ui= σi1Avi
可以通过公式推导得到上式的由来,为何特征值和奇异值之间满足那种关系,如何看待特征值分解和奇异值分解,如何对一个矩阵进行奇异值分解
A m ∗ n = U m ∗ m Σ m ∗ n V n ∗ n T A_{m*n} = \ U_{m*m}\Sigma_{m*n}V_{n*n}^{T} Am∗n= Um∗mΣm∗nVn∗nT
先给出如下结论:U是方阵AAT 的特征向量构成的正交矩阵,V是方阵ATA的特征向量构成的正交矩阵
( A T A ) v i = λ i v i \left( A^{T}A \right)v_{i} = \ \lambda_{i}v_{i} (ATA)vi= λivi
( A A T ) u i = λ i u i \left( AA^{T} \right)u_{i} = \ \lambda_{i}u_{i} (AAT)ui= λiui
简单推导:
A = U Σ V T A = U\Sigma V^{T} A=UΣVT
A T = V Σ T U T A^{T} = V\Sigma^{T}U^{T} AT=VΣTUT
因此有:
A T A = V Σ T U T UΣ V T = V Σ 2 V T A^{T}A = \ V\Sigma^{T}U^{T}\text{UΣ}V^{T} = \text{\ V}\Sigma^{2}V^{T} ATA= VΣTUTUΣVT= VΣ2VT
( A T A ) V = V Σ 2 V T V = Σ 2 V \left( A^{T}A \right)V = \ V\Sigma^{2}V^{T}V = \ \Sigma^{2}V (ATA)V= VΣ2VTV= Σ2V
这样便可以把V看成是方阵ATA的特征向量构成的正交矩阵,并且Σ2 构成了特征值,同理
A A T = UΣ V T V Σ T U T = U Σ 2 U T \ n ( A A T ) U = U Σ 2 U T U = Σ 2 U {AA^{T} = \ \text{UΣ}V^{T}V\Sigma^{T}U^{T} = \ U\Sigma^{2}U^{T}\backslash n}{\left( AA^{T} \right)U = U\Sigma^{2}U^{T}U = \ \Sigma^{2}U} AAT= UΣVTVΣTUT= UΣ2UT\n(AAT)U=UΣ2UTU= Σ2U
从此公式可以把U是方阵AAT 的特征向量构成的正交矩阵,并且Σ2 构成了特征值
根据上式可得到奇异值也有两种计算方式:
σ i = λ i \sigma_{i} = \ \sqrt{\lambda_{i}} σi= λi
σ i = A v i / u i \sigma_{i} = Av_{i}/u_{i} σi=Avi/ui
奇异值可以通过特征值取平方根直接求得,也可通过特征向量求得,这样我们便明白了奇异值和特征值之间的关联
4、谈PCA和SVD的关系
PCA通过特征矩阵W,将原始数据X降维到Z,其中X是m*n维,W是n*k维,Z是m*k维
Z = X W Z = XW Z=XW
其中转换特征矩阵W是原数据X的协方差矩阵XTX的前k个特征向量构成的,这样便完成了对数据的降维,而其实我们可以直接通过SVD完成对X降维到Z,看下面SVD分解:
X m ∗ n = U m ∗ k Σ k ∗ k V n ∗ k T X_{m*n} = \ U_{m*k}\Sigma_{k*k}V_{n*k}^{T} Xm∗n= Um∗kΣk∗kVn∗kT
X m ∗ n V n ∗ k = U m ∗ k Σ k ∗ k V n ∗ k T V n ∗ k X_{m*n}V_{n*k} = \ U_{m*k}\Sigma_{k*k}V_{n*k}^{T}V_{n*k} Xm∗nVn∗k= Um∗kΣk∗kVn∗kTVn∗k
X m ∗ n V n ∗ k = U m ∗ k Σ k ∗ k X_{m*n}V_{n*k} = \ U_{m*k}\Sigma_{k*k} Xm∗nVn∗k= Um∗kΣk∗k
可以看出我们直接将原数据X进行奇异值分解,X乘以右奇异矩阵V便可将m*n数据压缩到m*k的数据,完成对列的压缩,不需要进行特征值分解直接奇异值分解便可完成数据压缩,同理我们也可以按照下面方式对数据的行进行压缩:
X m ∗ n = U m ∗ k Σ k ∗ k V n ∗ k T X_{m*n} = \ U_{m*k}\Sigma_{k*k}V_{n*k}^{T} Xm∗n= Um∗kΣk∗kVn∗kT
U m ∗ k T X m ∗ n = U m ∗ k T U m ∗ k Σ k ∗ k V n ∗ k T {U_{m*k}}^{T}X_{m*n} = \ {U_{m*k}}^{T}U_{m*k}\Sigma_{k*k}V_{n*k}^{T} Um∗kTXm∗n= Um∗kTUm∗kΣk∗kVn∗kT
U m ∗ k T X m ∗ n = Σ k ∗ k V n ∗ k T {U_{m*k}}^{T}X_{m*n} = \Sigma_{k*k}V_{n*k}^{T} Um∗kTXm∗n=Σk∗kVn∗kT
列压缩是将数据特征进行压缩,列压缩是将相似的数据进行压缩,这样我们得出结论:可以直接对原数据X进行奇异值分解完成数据降维,不需要先由原数据X得到协方差矩阵求特征值得到转换特征矩阵再对数据进行降维
四、因子分析法FA
1、基本思想
因子分析法是数据降维的一种方法,因子分析法目的是找到原始变量的公共因子,然后用公共因子的线性组合来表示原始变量,举个例子:观察一个学生,统计出很多原始变量:代数、几何、语文、英语等各科的成绩,每天作业时间,每天笔记的量等等,通过这些现象寻找本质的因子,如公共因子有:逻辑因子、记忆因子、计算因子、表达因子
2、适用情况
在降维算法中,主成分分析法使用更广泛,PCA主要是通过数据的协方差矩阵得到数据的主特征向量方向,这便要求m>>n,m表示样本数、n表示特征数,即样本数要远大于特征数,这样协方差矩阵Σ满足是非奇异矩阵,特征向量是有解的。当样本数m和特征数n近似或者m 当然对于上述Σ不满秩的情况,我们可以限制Σ 但这种限制Σ会倒是大量特征信息丢失,因此在此情况下,我们可采用因子分析对数据降维 前验知识:在混合多元高斯分布中,如何求边缘高斯分布、条件高斯分布 联合多元随机变量x=[x1,x2] 的边缘高斯分布和条件高斯分布,其中x1属于Rr,x2属于Rm,则x属于Rr+m,则假设多元随机变量x服从均值为u,方差为Σ的高斯分布,可以得到x的符合的高斯分布形式为: u = [ u 1 u 2 ] u = \begin{bmatrix} u_{1} \\ u_{2} \\ \end{bmatrix} u=[u1u2] Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] \Sigma = \begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \\ \end{bmatrix} Σ=[Σ11Σ21Σ12Σ22] x1、x2称为联合多元高斯分布,则x1、x2的边缘高斯分布为: E ( x 1 ) = u 1 E ( x 2 ) = u 2 E\left( x_{1} \right) = \ u_{1}\text{\ E}\left( x_{2} \right) = \ u_{2} E(x1)= u1 E(x2)= u2 cov ( x 1 ) = E ( ( x 1 − u 1 ) ( x 1 − u 1 ) T ) = Σ 11 \text{cov}\left( x_{1} \right) = E\left( \left( x_{1} - u_{1} \right)\left( x_{1} - u_{1} \right)^{T} \right) = \ \Sigma_{11} cov(x1)=E((x1−u1)(x1−u1)T)= Σ11 cov ( x 2 ) = E ( ( x 2 − u 2 ) ( x 2 − u 2 ) T ) = Σ 22 \text{cov}\left( x_{2} \right) = E\left( \left( x_{2} - u_{2} \right)\left( x_{2} - u_{2} \right)^{T} \right) = \ \Sigma_{22} cov(x2)=E((x2−u2)(x2−u2)T)= Σ22 我们可以通过推导x的协方差分布得到x1、x2的协方差分布: cov ( x ) = Σ = [ E ( x − u ) ( x − u ) T ] \text{cov}\left( x \right) = \ \Sigma = \left\lbrack E\left( x - u \right){(x - u)}^{T} \right\rbrack cov(x)= Σ=[E(x−u)(x−u)T] = E ( ( x 1 − u 1 x 2 − u 2 ) ( x 1 − u 1 x 2 − u 2 ) T ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = E\left( \begin{pmatrix} x_{1} - u_{1} \\ x_{2} - u_{2} \\ \end{pmatrix}\begin{pmatrix} x_{1} - u_{1} \\ x_{2} - u_{2} \\ \end{pmatrix}^{T} \right) =E((x1−u1x2−u2)(x1−u1x2−u2)T) = E ( ( x 1 − u 1 ) ( x 1 − u 1 ) T ( x 1 − u 1 ) ( x 2 − u 2 ) T ( x 2 − u 2 ) ( x 1 − u 1 ) T ( x 2 − u 2 ) ( x 2 − u 2 ) T ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = E\begin{pmatrix} \left( x_{1} - u_{1} \right)\left( x_{1} - u_{1} \right)^{T} & \left( x_{1} - u_{1} \right)\left( x_{2} - u_{2} \right)^{T} \\ \left( x_{2} - u_{2} \right)\left( x_{1} - u_{1} \right)^{T} & \left( x_{2} - u_{2} \right)\left( x_{2} - u_{2} \right)^{T} \\ \end{pmatrix} =E((x1−u1)(x1−u1)T(x2−u2)(x1−u1)T(x1−u1)(x2−u2)T(x2−u2)(x2−u2)T) 这样我们便能够通过x得到x1和x2的边缘分布,即x1、x2边缘高斯分布满足: x 1 ∼ N ( u 1 , Σ 11 ) x_{1}\ \sim\ N(u_{1},\ \Sigma_{11}) x1 ∼ N(u1, Σ11) x 2 ∼ N ( u 2 , Σ 22 ) x_{2}\ \sim\ N(u_{2},\ \Sigma_{22}) x2 ∼ N(u2, Σ22) 同时我们也可以得出给定x2情况下x1的 条件高斯分布: x 1 ∣ x 2 ∼ N ( u 1 ∣ 2 , Σ 1 ∣ 2 ) x_{1}|x_{2}\ \sim\ N(u_{1|2},\ \Sigma_{1|2}) x1∣x2 ∼ N(u1∣2, Σ1∣2) 则条件高斯分布的均值和协方差分别是: u 1 ∣ 2 = u 1 + Σ 12 Σ 22 − 1 ( x 2 − u 2 ) u_{1|2} = \ u_{1} + \ \Sigma_{12}\Sigma_{22}^{- 1}(x_{2} - u_{2}) u1∣2= u1+ Σ12Σ22−1(x2−u2) Σ 1 ∣ 2 = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 \Sigma_{1|2} = \ \Sigma_{11} - \ \Sigma_{12}\Sigma_{22}^{- 1}\Sigma_{21} Σ1∣2= Σ11− Σ12Σ22−1Σ21 在下述的因子分析法建模中便用到了这里的边缘高斯分布和条件高斯分布 在因子分析法中,假设我们得到的原始数据为x,降维后的因子特征为z,x为n维的原始变量,z为k维的因子变量,我们找到原始数据x的因子变量z的线性组合,便完成将数据从n维降到k维,n>>k 首先给出因子分析法的假设模型: z ∼ N ( 0 , I ) z\ \sim\ N(0,\ I) z ∼ N(0, I) ε ∼ N ( 0 , ψ ) \varepsilon\sim N(0,\ \psi) ε∼N(0, ψ) x ∣ z ∼ N ( u + Λ z , ψ ) x|z\ \sim\ N(u + \Lambda z,\ \psi) x∣z ∼ N(u+Λz, ψ) x = u + Λ z + ε Λ ϵ R n ∗ k , z ϵ R k , x ϵ R n x = u + \Lambda z + \varepsilon\ \ \ \ \ \Lambda\epsilon R^{n*k},z\epsilon R^{k},x\epsilon R^{n} x=u+Λz+ε ΛϵRn∗k,zϵRk,xϵRn 我们假设z服从均值为0,协方差矩阵为单位矩阵的高斯分布,上面式子 x=u+⋀z+ε 即完成了低维数据z到高维数据x的一个映射,我们下面通过一个例子来看一下一维数据到二维数据的映射过程: 假设我们现在有一个一维的数据点z: 因子分析法目的便是用z代替x,那么如何求出x、z公式中的参数u、⋀、ψ,这里便用到了之前介绍的联合多元高斯分布的边缘高斯分布和条件高斯分布,这里我们把x、z看成联合多元高斯分布: [ z x ] ∼ N ( [ 0 u ] , [ I Λ T Λ Λ Λ T + ψ ] ) \begin{bmatrix} z \\ x \\ \end{bmatrix}\ \ \sim\ \ N(\begin{bmatrix} 0 \\ u \\ \end{bmatrix},\ \begin{bmatrix} I & \Lambda^{T} \\ \Lambda & \Lambda\Lambda^{T} + \psi\ \\ \end{bmatrix}\ ) [zx] ∼ N([0u], [IΛΛTΛΛT+ψ ] ) E [ ( x − E [ x ] ) ( x − E [ x ] ) T ] = Λ Λ T + ψ E\left\lbrack \left( x - E\left\lbrack x \right\rbrack \right)\left( x - E\left\lbrack x \right\rbrack \right)^{T} \right\rbrack = \ \Lambda\Lambda^{T} + \psi E[(x−E[x])(x−E[x])T]= ΛΛT+ψ 因此我们可以得到变量x的边缘高斯分布为: x ∼ N ( u , Λ Λ T + ψ ) x\ \sim\ N(u,\ \Lambda\Lambda^{T} + \psi) x ∼ N(u, ΛΛT+ψ) 因此利用最大似然法优化目标函数为: l ( u , Λ , Ψ ) = l o g ∏ i = 1 m 1 ( 2 π ) n / 2 ∣ Λ Λ T + ψ ∣ e x p ( − 1 2 ( x i − u ) T ( Λ Λ T + ψ ) T ( x i − u ) ) l(u,\ \Lambda,\Psi)\ = log\prod_{i = 1}^{m}{\frac{1}{{(2\pi)}^{n/2}|\Lambda\Lambda^{T} + \psi|}exp( - \frac{1}{2}{(x^{i} - u)}^{T}{(\Lambda\Lambda^{T} + \psi)}^{T}(x^{i} - u))} l(u, Λ,Ψ) =logi=1∏m(2π)n/2∣ΛΛT+ψ∣1exp(−21(xi−u)T(ΛΛT+ψ)T(xi−u)) 通过最大化上式,我们便可求得参数u、⋀、ψ,上式因为含有隐变量z无法直接求解,对于含有隐变量z的最大似然函数可通过EM算法求解 EM算法首先E-Step: Q i ( z i ) = p ( z i ∣ x i ; u , Λ , Ψ ) Q_{i}\left( z^{i} \right) = p(z^{i}|x^{i};u,\Lambda,\Psi) Qi(zi)=p(zi∣xi;u,Λ,Ψ) 根据条件高斯分布可得: z i ∣ x i ; u , Λ , Ψ ∼ N ( u z i ∣ x i , Σ z i ∣ x i ) z^{i}|x^{i};u,\Lambda,\Psi\ \sim N(u_{z^{i}|x^{i}},\ \Sigma_{z^{i}|x^{i}}) zi∣xi;u,Λ,Ψ ∼N(uzi∣xi, Σzi∣xi) 其中: u z i ∣ x i = Λ T ( Λ Λ T + ψ ) − 1 ( ( x i − u ) u_{z^{i}|x^{i}} = \ \Lambda^{T}{(\Lambda\Lambda^{T} + \psi)}^{- 1}((x^{i} - u) uzi∣xi= ΛT(ΛΛT+ψ)−1((xi−u) Σ z i ∣ x i = I − Λ T ( Λ Λ T + ψ ) − 1 Λ \Sigma_{z^{i}|x^{i}} = I - \ \Lambda^{T}{(\Lambda\Lambda^{T} + \psi)}^{- 1}\Lambda Σzi∣xi=I− ΛT(ΛΛT+ψ)−1Λ 于是便可得到: Q i ( z i ) = 1 ( 2 π ) n / 2 ∣ Σ z i ∣ x i ∣ 1 / 2 e x p ( − 1 2 ( x i − u z i ∣ x i ) T Σ z i ∣ x i − 1 ( x i − u z i ∣ x i ) ) Q_{i}\left( z^{i} \right) = \ \frac{1}{{(2\pi)}^{n/2}{|\Sigma_{z^{i}|x^{i}}|}^{1/2}}exp( - \frac{1}{2}{(x^{i} - u_{z^{i}|x^{i}})}^{T}{\Sigma_{z^{i}|x^{i}}}^{- 1}(x^{i} - u_{z^{i}|x^{i}})) Qi(zi)= (2π)n/2∣Σzi∣xi∣1/21exp(−21(xi−uzi∣xi)TΣzi∣xi−1(xi−uzi∣xi)) M-step优化目标函数,其中z满足高斯分布的连续变量,因此: ∑ i = 1 m ∫ Q i ( z i ) log p ( z i , x i ; u , Λ , Ψ ) Q i ( z i ) d z i \sum_{i = 1}^{m}{\int_{}^{}{Q_{i}\left( z^{i} \right)\log\frac{p(z^{i},\ x^{i};u,\Lambda,\Psi)}{Q_{i}\left( z^{i} \right)}}}dz^{i} i=1∑m∫Qi(zi)logQi(zi)p(zi, xi;u,Λ,Ψ)dzi 这样再对各个参数求偏导,然后不断迭代E步和M步求得参数 u、⋀、ψ 下面再简单提几个实际工程中也常用到的数据降维的方式的思想,不做详细讨论,仅供参考! (1) 图表示的是主成分分析PCA对特征方向的选取 在构建模型前,对数据进行探索性分析必不可少。但在浏览数据的过程中,有时候我们会发现其中包含不少缺失值。如果缺失值少,我们可以填补缺失值或直接删除这个变量;当缺失值在数据集中的占比过高时,一般会选择直接删除这个变量,因为它包含的信息太少了。但具体删不删、怎么删需要视情况而定,我们可以设置一个阈值,如果缺失值占比高于阈值,删除它所在的列。阈值越高,降维方法越积极,通过删除无效缺失值完成数据降维 如果我们有一个数据集,其中某列的数值基本一致,也就是它的方差非常低,那么这个变量还有价值吗?我们通常认为低方差变量携带的信息量也很少,所以可以把它直接删除。放到实践中,就是先计算所有变量的方差大小,然后删去其中最小的几个。需要注意的一点是:方差与数据范围相关的,因此在采用该方法前需要对数据做归一化处理 如果两个变量之间是高度相关的,这意味着它们具有相似的趋势并且可能携带类似的信息。同理,这类变量的存在会降低某些模型的性能(例如线性和逻辑回归模型)。为了解决这个问题,我们可以计算独立数值变量之间的相关性。如果相关系数超过某个阈值,就删除其中一个变量。作为一般准则,我们应该保留那些与目标变量显示相当或高相关性的变量 本文完结,后续将其他降维算法以及对降维算法实际实现进行讨论,创作不易,转载请注明出处,谢谢! 如需获得本文的word和pdf版本,请关注以下公众号并回复关键字:降维算法
(1) 限制Σ是对角阵,即Σ出对角元素不为0外其他均为0
(2) 在(1)的基础上,要求对角元素均相等
3、因子分析法前验知识
4、因子分析法建模
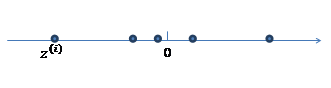
通过变换 ⋀z,其中⋀属于R2*1,便将一维数据为映射到二维:

然后再在数据上加上均值u,即u+⋀z,对数据进行一个平移操作:

最后,我们再加上 ε 的误差扰动,使得数据点可以不在线上,ε 是符合高斯分布的误差,这样即得到了映射到了高维数据x:

同理,我们只要找到了原始数据x的低维公共因子z的线性组合便完成了数据降维
5、因子分析法EM算法求解
五、独立成分分析ICA
先用一张图客观理解一下ICA降维方法,在下图中
(2) 图表示的是独立成分分析ICA对特征方向选取

六、缺失值比率
七、低方差滤波
八、高相关滤波
