hashcode,有点讲究
什么是好的hashcode,一般来说,一个hashcode,一般用int来表示,32位。
下面两个hashcode,大家觉得怎么样?
0111 1111 1111 1111 1111 1111 1111 1111 ------A
1111 1111 1111 1111 1111 1111 1111 1111 ------B
只有第32位(从右到左)不一样,好像也没有所谓的好坏吧?
那,我们再想想,hashcode一般怎么使用呢?在hashmap中,由数组+链表+红黑树组成,其中,数组乃重中之重,假设数组长度为2的n次方,(hashmap的数组,强制要求长度为2的n次方),这里假设为8.
大家又知道,hashcode 对 8 取模,效果等同于 hashcode & (8 - 1)。
那么,前面的A 和 (8 - 1)相与的结果如何呢?
0111 1111 1111 1111 1111 1111 1111 1111 ------A
0000 0000 0000 0000 0000 0000 0000 0111 ------ 8 -1
相与
0000 0000 0000 0000 0000 0000 0000 0111 ------ 7
结果为7,也就是,会放进array[7]。
大家再看B的计算过程:
1111 1111 1111 1111 1111 1111 1111 1111 ------B
0000 0000 0000 0000 0000 0000 0000 0111 ------ 8 -1
相与
0000 0000 0000 0000 0000 0000 0000 0111 ------ 7
虽然B的第32位为1,但是,奈何和我们相与的队友,7,是个垃圾。
前面的高位,全是0。
ok,你懂了吗,数组长度太小了,才8,导致前面有29位都是0;你可能觉得一般容量不可能这么小,那假设容量为2的16次方,容量为65536,这下不是很小了吧,但即使如此,前面的16位也是0.
所以,问题明白了吗,我们计算出来的hashcode,低位相同,高位不同;但是,因为和我们进行与计算的队友太过垃圾,导致我们出现了hash冲突。
ok,我们怎么来解决这个问题呢?
我们能不能把高位也参与计算呢?自然,是可以的。
hashmap中如何优化
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
这里,其实分了3个步骤:
-
计算hashcode,作为操作数1
h = key.hashCode() -
将第一步的hashcode,右移16位,作为操作数2
h >>> 16 -
操作数1 和 操作数2 进行异或操作,得到最终的hashcode
还是拿前面的来算,
0111 1111 1111 1111 1111 1111 1111 1111 ------A
0000 0000 0000 0000 0111 1111 1111 1111 ----- A >>> 16
异或(相同则为0,否则为1)
0111 1111 1111 1111 1000 0000 0000 0000 --- 2147450880
这里算出来的结果是 2147450880,再去对 7 进行与运算:
0111 1111 1111 1111 1000 0000 0000 0000 --- 2147450880
0000 0000 0000 0000 0000 0000 0000 0111 ------ 8 -1
与运算
0000 0000 0000 0000 0000 0000 0000 0000 ------ 0
这里的A,算出来,依然在array[0]。
再拿B来算一下:
1111 1111 1111 1111 1111 1111 1111 1111 ------ B
0000 0000 0000 0000 1111 1111 1111 1111 ----- B >>> 16
异或(相同则为0,否则为1)
1111 1111 1111 1111 0000 0000 0000 0000 --- -65536
0000 0000 0000 0000 0000 0000 0000 0111 ------ 7
与运算
0000 0000 0000 0000 0000 0000 0000 0000 ------- 0
最终算出来为0,所以,应该放在array[0]。
恩?算出来两个还是冲突了,我只能说,我挑的数字真的牛逼,是不是该去买彩票啊。。
总的来说,大家可以多试几组数,下边提供下源代码:
public class BinaryTest {
public static void main(String[] args) {
int a = 0b00001111111111111111111111111011;
int b = 0b10001101111111111111110111111011;
int i = tabAt(32, a);
System.out.println("index for a:" + i);
i = tabAt(32, b);
System.out.println("index for b:" + i);
}
static final int tabAt(int arraySize, int hash) {
int h = hash;
int finalHashCode = h ^ (h >>> 16);
int i = finalHashCode & (arraySize - 1);
return i;
}
}
虽然说,我测试了几个数字,还是有些冲突,但是,你把高16位弄进来参与计算,总比你不弄进来计算要好吧。
大家也可以看看hashmap中,hash方法的注释:
/** * Computes key.hashCode() and spreads (XORs) higher bits of hash * to lower. Because the table uses power-of-two masking, sets of * hashes that vary only in bits above the current mask will * always collide. (Among known examples are sets of Float keys * holding consecutive whole numbers in small tables.) So we * apply a transform that spreads the impact of higher bits * downward. There is a tradeoff between speed, utility, and * quality of bit-spreading. Because many common sets of hashes * are already reasonably distributed (so don't benefit from * spreading), and because we use trees to handle large sets of * collisions in bins, we just XOR some shifted bits in the * cheapest possible way to reduce systematic lossage, as well as * to incorporate impact of the highest bits that would otherwise * never be used in index calculations because of table bounds. */
里面提到了2点:
So we apply a transform that spreads the impact of higher bits downward.
所以,我们进行了一个转换,把高位的作用利用起来。
we just XOR some shifted bits in the cheapest possible way to reduce systematic lossage, as well as
to incorporate impact of the highest bits that would otherwise never be used in index calculations because of table bounds.
我们仅仅异或了从高位移动下来的二进制位,用最经济的方式,削减系统性能损失,同样,因为数组大小的限制,导致高位在索引计算中一直用不到,我们通过这种转换将其利用起来。
ConcurrentHashMap如何优化
在concurrentHashMap中,其主要是:
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
这里主要是使用spread方法来计算hash值:
static final int spread(int h) {
return (h ^ (h >>> 16)) & HASH_BITS;
}
大家如果要仔细观察每一步的二进制,可以使用下面的demo:
static final int spread(int h) {
// 1
String s = Integer.toBinaryString(h);
System.out.println("h:" + s);
// 2
String lower16Bits = Integer.toBinaryString(h >>> 16);
System.out.println("lower16Bits:" + lower16Bits);
// 3
int temp = h ^ (h >>> 16);
System.out.println("h ^ (h >>> 16):" + Integer.toBinaryString(temp));
// 4
int result = (temp) & HASH_BITS;
System.out.println("final:" + Integer.toBinaryString(result));
return result;
}
这里和HashMap相比,多了点东西,也就是多出来了:
& HASH_BITS;
这个有什么用处呢?
因为(h ^ (h >>> 16))计算出来的hashcode,可能是负数。这里,和 HASH_BITS进行了相与:
static final int HASH_BITS = 0x7fffffff; // usable bits of normal node hash
1111 1111 1111 1111 1111 1111 1111 1111 假设计算出来的hashcode为负数,因为第32位为1
0111 1111 1111 1111 1111 1111 1111 1111 0x7fffffff
进行相与
0111 ..................................
这里,第32位,因为0x7fffffff的第32位,总为0,所以相与后的结果,第32位也总为0 ,所以,这样的话,hashcode就总是正数了,不会是负数。
concurrentHashMap中,node的hashcode,为啥不能是负数
当hashcode为正数时,表示该哈希桶为正常的链表结构。
当hashcode为负数时,有几种情况:
ForwardingNode
此时,其hash值为:
static final int MOVED = -1; // hash for forwarding nodes
当节点为ForwardingNode类型时(表示哈希表在扩容进行中,该哈希桶已经被迁移到了新的临时hash表,此时,要get的话,需要去临时hash表查找;要put的话,是不行的,会帮助扩容)
TreeBin
static final int TREEBIN = -2; // hash for roots of trees
表示,该哈希桶,已经转了红黑树。
扩容时的位运算
/**
* Returns the stamp bits for resizing a table of size n.
* Must be negative when shifted left by RESIZE_STAMP_SHIFT.
*/
static final int resizeStamp(int n) {
return Integer.numberOfLeadingZeros(n) | (1 << (RESIZE_STAMP_BITS - 1));
}
这里,假设,n为4,即,hashmap中数组容量为4.
-
下面这句,求4的二进制表示中,前面有多少个0.
Integer.numberOfLeadingZeros(n)
表示为32位后,如下
0000 0000 0000 0000, 0000 0000 0000 0100
所以,前面有29个0,即,这里的结果为29.
-
(1 << (RESIZE_STAMP_BITS - 1)
这一句呢,其中RESIZE_STAMP_BITS 是个常量,为16. 相当于,把1 向左移动15位。
二进制为:
1000 0000 0000 0000 -- 1 << 15
最终结果:
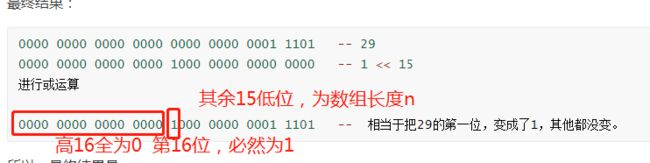
0000 0000 0000 0000 0000 0000 0001 1101 -- 29
0000 0000 0000 0000 1000 0000 0000 0000 -- 1 << 15
进行或运算
0000 0000 0000 0000 1000 0000 0001 1101 -- 相当于把29的第一位,变成了1,其他都没变。
所以,最终结果是,
这个数,换算为10进制,为32972,是个正数。
这个数,有啥用呢?
在addCount函数中,当整个哈希表的键值对数量,超过sizeCtl时(一般为0.75 * 数组长度),就会触发扩容。
java.util.concurrent.ConcurrentHashMap#addCount
int sc = sizeCtl;
boolean bSumExteedSizeControl = newBaseCount >= (long) sc;
// 1
if (bContinue) {
int rs = resizeStamp(n);
// 2
if (sc < 0) {
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
// 3
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
newBaseCount = sumCount();
} else {
break;
}
-
1处,如果扩容条件满足
-
2处,如果sc小于0,这个sc是啥,就是前面说的sizeCtl,此时应该是等于:0.75 * 数组长度,不可能为负数
-
3处,将sc(此时为正数),cas修改为:
(rs << RESIZE_STAMP_SHIFT) + 2)这个数有点意思了,rs就是前面我们的resizeStamp得到的结果。
按照前面的demo,我们拿到的结果为:
0000 0000 0000 0000 1000 0000 0001 1101 -- 相当于把29的第一位,变成了1,其他都没变。因为
private static int RESIZE_STAMP_BITS = 16; private static final int RESIZE_STAMP_SHIFT = 32 - RESIZE_STAMP_BITS;所以,RESIZE_STAMP_SHIFT 为16.
0000 0000 0000 0000 1000 0000 0001 1101 -- 相当于把29的第一位,变成了1,其他都没变。 1000 0000 0001 1101 0000 0000 0000 0000 --- 左移16位,即 rs << RESIZE_STAMP_SHIFT 1000 0000 0001 1101 0000 0000 0000 0010 -- (rs << RESIZE_STAMP_SHIFT) + 2)最终,这个数,第一位是 1,说明了,这个数,肯定是负数。
大家如果看过其他人写的资料,也就知道,当sizeCtl为负数时,表示正在扩容。
所以,这里
if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2))这句话就是,如果当前线程成功地,利用cas,将sizeCtl从正数,变成负数,就可以进行扩容。
扩容时,其他线程怎么执行
// 1 if (bContinue) { int rs = resizeStamp(n); // 2 if (sc < 0) { // 2.1 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; // 2.2 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } // 3 else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); newBaseCount = sumCount(); } else { break; }此时,因为上面的线程触发了扩容,sc已经变成了负数了,此时,新的线程进来,会判断2处。
2处是满足的,会进入2.1处判断,这里的部分条件看不懂,大概是:扩容已经结束,就不再执行,直接break
否则,进入2.2处,辅助扩容,同时,把sc变成sc + 1,增加扩容线程数。
总结
时间仓促,如有问题,欢迎指出。