计算机图形学第五章---基本图形生成算法

 

第五章 基本图形生成算法

如何在指定的输出设备上根据坐标描述构造基本二维几何图形（点、直线、圆、椭圆、多边形域、字符串及其相关属性等）。

 

图形生成的概念

图形的生成：是在指定的输出设备上，根据坐标描述构造二维几何图形。

图形的扫描转换：在光栅显示器等数字设备上确定一个最佳逼近于图形的象素集的过程。

 

直线段的扫描转换

直线的绘制要求

  （1）直线要直；

  （2）直线的端点要准确，无定向性无断裂；

  （3）直线的亮度、色泽要均匀；

  （4）画线的速度要快；

  （5）具有不同的色泽、亮度、线型等。

解决的问题：给定直线两端点P0(x0,y0)和P1(x1,y1)，画出该直线。

 

数值微分法(DDA法):

增量算法

直观、易实现

不利于用硬件实现

 

 

中点Bresenhan算法:

算法原理：根据直线的斜率确定或选择变量在x或y方向上每次递增一个单位，而另一方向的增量为1或0，它取决于实际直线与相邻象素点的距离，这一距离称为误差项。

 

中点Bresenham算法——算法步骤

输入直线的两端点P0(x0,y0)和P1(x1,y1)。

计算初始值△x、△y、D=△x-2△y、x=x0、y=y0。

绘制点(x,y)。判断D的符号。若D<0，则(x,y)更新为(x+1,y+1)，D更新为D+2△x-2△y；否则(x,y)更新为(x+1,y), D更新为D-2△y。

当直线没有画完时，重复上一步骤，否则结束。

 

改进的Bresenhan算法——算法步骤

1.输入直线的两端点P0(x0,y0)和P1(x1,y1)。

2.计算初始值△x、△y、e=-△x、x=x0、y=y0。

3.绘制点(x,y)。

4.e更新为e+2△y，判断e的符号。若e>0，则(x,y)更新为(x+1,y+1)，同时将e更新为e-2△x；否则(x,y)更新为(x+1,y)。

5.当直线没有画完时，重复步骤3和4。否则结束。

 

圆的扫描转换

解决的问题：绘出圆心在原点，半径为整数R的圆x2+y2=R2。

 

简单方程产生圆弧:

算法原理：利用其函数方程，直接离散计算。

 

中点Bresenham画圆——算法步骤

1.输入圆的半径R。

2.计算初始值d=1-R、x=0、y=R。

3.绘制点(x,y)及其在八分圆中的另外七个对称点。

4.判断d的符号。若d<0，则先将d更新为d+2x+3，再将(x,y)更新为(x+1,y)；否则先将d更新为d+2(x-y)+5，再将(x,y)更新为(x+1,y-1)。

5.当x时，重复步骤3和4。否则结束。

 

多边形的扫描转换与区域填充:

多边形的扫描转换主要是通过确定穿越区域的扫描线的覆盖区间来填充。

区域填充是从给定的位置开始涂描直到指定的边界条件为止。

 

 

多边形的扫描转换:

顶点表示用多边形的顶点序列来刻划多边形。

点阵表示是用位于多边形内的象素的集合来刻划多边形。

扫描转换多边形：从多边形的顶点信息出发，求出位于其内部的各个象素，并将其颜色值写入帧缓存中相应单元的过程。

 

X－扫描线算法——原理

基本思想：按扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的所有象素。

 

X－扫描线算法——算法步骤

1.确定多边形所占有的最大扫描线数，得到多边形顶点的最小和最大y值（ymin和ymax）。

2.从y=ymin到y=ymax，每次用一条扫描线进行填充。

3.对一条扫描线填充的过程可分为四个步骤：

       求交；排序；交点配对；区间填色。

 

X－扫描线算法——取整规则

交点的取整规则：使生成的像素全部位于多边形之内。（用于直线等图元扫描转换的四舍五入原则可能导致部分像素位于多边形之外，从而不可用）。

假定非水平边与扫描线y=e相交，交点的横坐标为x，规则如下：

 规则1：X为小数，即交点落于扫描线上两个相邻像素之间时：

交点位于左边界之上，向右取整；

交点位于右边界之上，向左取整；

 规则2：边界上象素的取舍问题，避免填充扩大化。规定落在右边边界上的像素不予填充。（具体实现时，只要对扫描线与多边形的相交区间左闭右开）

规则3：当扫描线与多边形顶点相交时，交点的取舍，保证交点正确配对。

解决方法：

    当扫描线与多边形的顶点相交时，

若共享顶点的两条边分别落在扫描线的两边，交点只算一个；

若共享顶点的两条边在扫描线的同一边，这时交点作为零个或两个。

实际处理：只要检查顶点的两条边的另外两个端点的Y值，两个Y值中大于交点Y值的个数是0，1，2，来决定取0，1，2个交点。

 

 

改进的有效边表算法:

改进原理：

处理一条扫描线时，仅对有效边求交。

利用扫描线的连贯性。

利用多边形边的连贯性。

 

改进的有效边表算法（Y连贯性算法）

有效边（Active Edge）：指与当前扫描线相交的多边形的边，也称为活性边。

有效边表（Active Edge Table, AET）：把有效边按与扫描线交点x坐标递增的顺序存放在一个链表中，此链表称为有效边表。

有效边表的每个结点：

            x  ymax  1/k  next

 

改进的有效边表算法——构造边表

首先构造一个纵向链表，链表的长度为多边形所占有的最大扫描线数，链表的每个结点，称为一个桶，则对应多边形覆盖的每一条扫描线

 

。

将每条边的信息链入与该边最小y坐标（ymin ）相对应的桶处。也就是说，若某边的较低端点为ymin，则该边就放在相应的扫描线桶中。

每条边的数据形成一个结点，内容包括：该扫描线与该边的初始交点x（即较低端点的x值），1/k，以及该边的最大y值ymax。

x|ymin   ymax  1/k   NEXT

同一桶中若干条边按X|ymin由小到大排序，若X|ymax 相等，则按照1/k由小到大排序。

 

改进的有效边表算法——算法步骤

(1)初始化：构造边表，AET表置空；

(2)将第一个不空的ET表中的边与AET表合并；

(3)由AET表中取出交点对进行填充。填充之后删除y=ymax的边；

(4)yi+1=yi+1,根据xi+1=xi+1/k计算并修改AET表，同时合并ET表中y=yi+1桶中的边，按次序插入到AET表中，形成新的AET表；

(5)AET表不为空则转(3)，否则结束。

 

 

 

边缘填充算法:

基本思想：按任意顺序处理多边形的每条边。处理时，先求出该边与扫描线的交点，再对扫描线上交点右方的所有象素取反。

算法简单，但对于复杂图型，每一象素可能被访问多次

 

栅栏填充算法:

栅栏指的是一条过多边形顶点且与扫描线垂直的直线。它把多边形分为两半。

基本思想：按任意顺序处理多边形的每一条边，但处理每条边与扫描线的交点时，将交点与栅栏之间的象素取反。

这种算法尽管减少了被重复访问象素的数目，但仍有一些象素被重复访问。

 

边标志算法:

基本思想：先用特殊的颜色在帧缓存中将多边形的边界勾画出来，然后将着色的象素点依x坐标递增的顺序配对，再把每一对象素构成的区间置为填充色。

分为两个步骤：打标记；填充。

当用软件实现本算法时，速度与改进的有效边表算法相当，但本算法用硬件实现后速度会有很大提高。

 

 

区域填充

基本概念:

区域填充是指从区域内的某一个象素点（种子点）开始，由内向外将填充色扩展到整个区域内的过程。

区域是指已经表示成点阵形式的填充图形，它是相互连通的一组像素的集合。

 

区域的表示方法:

边界表示法：把位于给定区域的边界上的象素一一列举出来的方法。

边界表示法中，由于边界由特殊颜色指定，填充算法可以逐个象素地向外处理，直到遇到边界颜色为止，这种方法称为边界填充算法（Boundary-fill Algorithm）。

 内点表示法：枚举出给定区域内所有象素的表示方法。以内点表示法为基础的区域填充算法称为泛填充算法（Flood-fill Algorithm）。

 

区域的分类:

4-连通区域：从区域上的一点出发，通过访问已知点的4-邻接点，在不越出区域的前提下，遍历区域内的所有象素点。

8-连通区域：从区域上的一点出发，通过访问已知点的8-邻接点，在不越出区域的前提下，遍历区域内的所有象素点。

 

4连通与8连通区域的区别:

连通性： 4连通可看作8连通区域，但对边界有要求。

对边界的要求。

 

区域填充算法:

区域填充算法（边界填充算法和泛填充算法）是根据区域内的一个已知象素点（种子点）出发，找到区域内其他象素点的过程，所以把这一类算法也成为种子填充算法。

 

算法的输入：种子点坐标(x,y)，填充色以及边界颜色。

利用堆栈实现简单的种子填充算法

      算法从种子点开始检测相邻位置是否是边界颜色，若不是就用填充色着色，并检测该像素点的相邻位置，直到检测完区域边界颜色范围内的所有像素为止。

 

栈结构实现4-连通边界填充算法的算法步骤为：

    种子象素入栈；当栈非空时重复执行如下三步操作：

    (a)栈顶象素出栈；

    (b)将出栈象素置成填充色；

    (c)检查出栈象素的4-邻接点，若其中某个象素点不是边界色且未置成多边形色，则把该象素入栈。

 

栈结构实现8-连通边界填充算法的算法步骤为：

           种子象素入栈；当栈非空时重复执行如下三步操作：

          (a)栈顶象素出栈；

          (b)将出栈象素置成填充色；

          (c)检查出栈象素的8-邻接点，若其中某个像素点不是边界色且未置成多边形色，则把该像素入栈。可以用于填充带有内孔的平面区域。

把太多的像素压入堆栈，降低了效率，同时需要较大的存储空间。

递归执行，算法简单，但效率不高，区域内每一像素都引起一次递归，进/出栈费时费内存。

通过沿扫描线填充水平象素段，来代替处理4-邻接点和8-邻接点。

 

扫描线种子填充算法：扫描线通过在任意不间断扫描线区间中只取一个种子像素的方法使堆栈的尺寸极小化。不间断区间是指在一条扫描线上的一组相邻像素。

 

基本过程：当给定种子点时，首先填充种子点所在的扫描线上的位于给定区域的一个区段，然后确定与这一区段相通的上下两条扫描线上位于给定区域内的区段，并依次保存下来。反复这个过程，直到填充结束。

 

区域填充算法——泛填充算法

算法的输入：种子点坐标(x,y)，填充色和内部点的颜色。

算法原理：算法从指定的种子(x,y)开始，用所希望的填充颜色赋给所有当前为给定内部颜色的象素点。种子象素入栈；栈非空时重复执行如下三步操作：

     (1)栈顶象素出栈；

     (2)将出栈象素置成填充色；

     (3)检查出栈象素的8-邻接点，若其中某个象素点不是给定内部点的颜色且未置成新的填充色，则把该象素入栈。

 

当以边界表示时，4-连通边界填充算法只能填充4-连通区域，8-连通边界填充算法也只能填充8-连通区域。

当以内点表示时，8-连通泛填充算法可以填充8-连通区域也可以填充4-连通区域，当然4-连通泛填充算法还是只能填充4-连通区域。

 

相关概念

相关概念——内外测试

奇-偶规则（Odd-even Rule）

          从任意位置p作一条射线，若与该射线相交的多边形边的数目为奇数，则p是多边形内部点，否则是外部点。

非零环绕数规则（Nonzero Winding Number Rule）

首先使多边形的边变为矢量。

将环绕数初始化为零。

再从任意位置p作一条射线。当从p点沿射线方向移动时，对在每个方向上穿过射线的边计数，每当多边形的边从右到左穿过射线时，环绕

 

数加1，从左到右时，环绕数减1。

处理完多边形的所有相关边之后，若环绕数为非零，则p为内部点，否则，p是外部点。

 

相关概念——曲线边界区域填充

相交计算中包含了非线性边界。

对于简单曲线：

       （1）计算曲线相对两侧的两个扫描线交点

       （2）简单填充在曲线两侧上的边界点间的水平象素区间。

 

 

属性处理

图素或图段的外观由其属性决定。

图形软件中实现属性选择的方法是提供一张系统当前属性值表，通过调用标准函数提供属性值表的设置和修改。进行扫描转换时，系统使用属性值表中的当前属性值进行显示和输出。

 

线型的显示可用象素段方法实现：针对不同的线型，画线程序沿路径输出一些连续象素段，在每两个实心段之间有一段中间空白段，他们的长度（象素数目）可用象素模板(pixel mask)指定。

存在问题：如何保持任何方向的划线长度近似地相等。

 

 

反走样技术:

用离散量表示连续量引起的失真，就叫做走样（Aliasing）。

产生原因：

    数学意义上的图形是由无线多个连续的、面积为零的点构成；但在光栅显示器上，用有限多个离散的，具有一定面积的象素来近似地表示他们。

走样现象：

一是光栅图形产生的阶梯形。

一是图形中包含相对微小的物体时，这些物体在静态图形中容易被丢弃或忽略，在动画序列中时隐时现，产生闪烁。

 

用于减少或消除这种效果的技术，称为反走样（antialiasing，图形保真）。

 

过取样：在高于显示分辨率的较高分辨率下用点取样方法计算，然后对几个象素的属性进行平均得到较低分辨率下的象素属性。

 

简单过取样

    在x，y方向把分辨率都提高一倍，使每个象素对应4个子象素，然后扫描转换求得各子象素的颜色亮度，再对4个象素的颜色亮度进行平均，得到较低分辨率下的象素颜色亮度。

 

重叠过取样：为了得到更好的效果，在对一个像素点进行着色处理时，不仅仅只对其本身的子像素进行采样，同时对其周围的多个像素的子像素进行采样，来计算该点的颜色属性。

 

 

基于加权模板的过取样：前面在确定像素的亮度时，仅仅是对所有子像素的亮度进行简单的平均。更常见的做法是给接近像素中心的子像素赋予较大的权值，即对所有子像素的亮度进行加权平均。

 

反走样——简单的区域取样:

在整个像素区域内进行采样，这种技术称为区域取样。又由于像素的亮度是作为一个整体被确定的，不需要划分子像素，故也被称为前置滤波。

 

可以利用一种求相交区域的近似面积的离散计算方法：

        (1)将屏幕像素分割成n个更小的子像素，

        (2)计算中心落在直线段内的子像素的个数m，

        (3)m/n为线段与像素相交区域面积的近似值。

直线段对一个像素亮度的贡献与两者重叠区域的面积成正比。

相同面积的重叠区域对像素的贡献相同。

 

反走样——加权区域取样

过取样中，我们对所有子像素的亮度进行简单平均或加权平均来确定像素的亮度。

在区域取样中，我们使用覆盖像素的连续的加权函数（Weighting Function）或滤波函数(Filtering Function)来确定像素的亮度。

 

加权区域取样原理:

       加权函数W(x,y)是定义在二维显示平面上的函数。对于位置为(x,y)的小区域dA来说，函数值W(x,y)（也称为在(x,y)处的高度）表示小区域dA的权值。将加权函数在整个二维显示图形上积分，得到具有一定体积的滤波器（Filter），该滤波器的体积为1。将加权函数在显示图形上进行积分，得到滤波器的一个子体，该子体的体积介于0到1之间。用它来表示像素的亮度。

 

特点：

接近理想直线的象素将被分配更多的灰度值；

相邻两个象素的滤波器相交，有利于缩小直线条上相邻象素的灰度差。

 

 

 

在OpenGL中绘制图形

点的绘制:

         glBegin(GL_POINTS)；

             glVertex3f(0.0f, 0.0f, 0.0f);

             glVertex3f(10.0f, 0.0f, 0.0f);

         glEnd()；

点的属性（大小）

         void glPointSize(GLfloat size)；

 

直线的绘制:

直线的绘制模式

GL_LINES

GL_LINE_STRIP

GL_LINE_LOOP

直线的属性

线宽

        void glLineWidth(GLfloat width)

线型

        glEnable(GL_LINE_STIPPLE)；

        glLineStipple(GLint factor，GLushort pattern)；

 

多边形面的绘制:

GL_TRIANGLES

GL_TRIANGLE_STRIP

GL_TRIANGLE_FAN

四边形面的绘制

GL_QUADS

GL_QUADS_STRIP

多边形面的绘制（GL_POLYGON）

 

多边形面的绘制规则:

所有多边形都必须是平面的。

多边形的边缘决不能相交，而且多边形必须是凸的。

解决：对于非凸多边形，可以把它分割成几个凸多边形（通常是三角形），再将它绘制出来。

 

问题：轮廓图形状态会看到组成大表面的所有小三角形。处理OpenGL提供了一个特殊标记来处理这些边缘，称为边缘标记。

                     glEdgeFlag（True）

                     glEdgeFlag（False）

 

多边形面的正反属性（绕法）

            指定顶点时顺序和方向的组合称为“绕法”。绕法是任何多边形图元的一个重要特性。一般默认情况下，OpenGL认为逆时针绕法的多边形是正对着的。

            glFrontFace(GL_CW)；

 

多边形面的颜色:

 glShadeModel(GL_FLAT) 用指定多边形最后一个顶点时的当前颜色作为填充多边形的纯色，唯一例外是GL_POLYGON图元，它采用的是第一个顶点的颜色。

 glShadeModel(GL_SMOOTH) 从各个顶点给三角形投上光滑的阴影，为各个顶点指定的颜色之间进行插值。

 

多边形面的显示模式:

            glPolygonMode(GLenum face，GLenum mode)；

参数face用于指定多边形的哪一个面受到模式改变的影响。

参数mode用于指定新的绘图模式。

 

 

多边形面的填充:

         多边形面既可以用纯色填充，也可以用32×32的模板位图来填充。

            void glPolygonStipple(const GLubyte *mask);

            glEnable(GL_POLYGON_STIPPLE);

 

多边形面的法向量:

法向量是垂直于面的方向上点的向量，它确定了几何对象在空间中的方向。

在OpenGL中，可以为每个顶点指定法向量。

        void glNormal3{bsidf} ( TYPE nx, TYPE ny, TYPE nz);

        void glNormal3{bsidf}v (const TYPE* v);

 

OpenGL中的字符函数:

GLUT位图字符

          void glutBitmapCharacter(void *font, int character);

GLUT矢量字符

           void glutStrokeCharacter(void *font, int character);

 

OpenGL中的反走样:

启用反走样

        glEnable(primitiveType);

启用OpenGL颜色混和并指定颜色混合函数

         glEnable(GL_BLEND);

         glBlendFunc(GL_SCR_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

 

 

颜色混和函数用于计算两个相互重叠的对象的颜色。

在RGBA颜色模式（A表示透明度）中，已知源像素的颜色值为（Sr，Sg，Sb，Sa），目标像素的颜色值为（Dr，Dg，Db，Da），颜色混合后像素的颜色为：

        （RS·Sr +RD·Dr，GS·Sg +GD·Dg，BS·Sb +BD·Db，AS·Sa +AD·Da）

 

 

定义混合因子

          void glBlendFunc(GLenum srcfactor, GLenum destfactor);

常量	RGB混合因子	Alpha混合因子
GL_ZERO	(0，0，0)	0
GL_ONE	(1，1，1)	1
GL_SRC_COLOR	（RS，GS，BS）	AS
GL_ONE_MINUS_SRC_COLOR	(1，1，1)－（RS，GS，BS）	1－AS
GL_DST_COLOR	（RD，GD，BD）	AD
GL_ONE_MINUS_DST_COLOR	(1，1，1)－（RD，GD，BD）	1－AD
GL_SCR_ALPHA	(AS，AS，AS)	AS
GL_ONE_MINUS_SRC_ ALPHA	(1，1，1)－(AS，AS，AS)	1－AS
GL_DST_ALPHA	(AD，AD，AD)	AD
GL_ONE_MINUS_DST_ ALPHA	(1，1，1)－(AD，AD，AD)	1－AD

 

 

#include
GLuint lineList; //指定显示列表ID
void Initial()
{
 glClearColor(1.0f, 1.0f, 1.0f, 0.0f);
 glLineWidth(12.0f);
 glColor4f (0.0, 0.6, 1.0, 1.0);
 lineList = glGenLists(1);
 glNewList(lineList, GL_COMPILE);  //定义显示列表
  glBegin(GL_LINE_LOOP);
   glVertex2f(1.0f, 1.0f);
   glVertex2f(4.0f, 2.0f);
   glVertex2f(2.0f, 5.0f);
  glEnd();
 glEndList();
}

void ChangeSize(GLsizei w, GLsizei h)
{
 if(h == 0)  h = 1;
    glViewport(0, 0, w, h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 if(w<=h)
  gluOrtho2D(0.0, 5.0, 0.0, 6.0*(GLfloat)h/(GLfloat)w);
 else
  gluOrtho2D(0.0, 5.0*(GLfloat)w/(GLfloat)h, 0.0, 6.0);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
}

void Displayt(void)
{ 
 glClear(GL_COLOR_BUFFER_BIT);
 glCallList(lineList);
    glFlush();
}

void Displayw(void)
{
 glClear(GL_COLOR_BUFFER_BIT);
 glEnable(GL_LINE_SMOOTH);      //使用反走样
 glEnable (GL_BLEND);             //启用混合函数
 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);  //指定混合函数
 glCallList(lineList);
    glFlush();
}

void main(void)
{
 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
 glutInitWindowSize(300, 300);
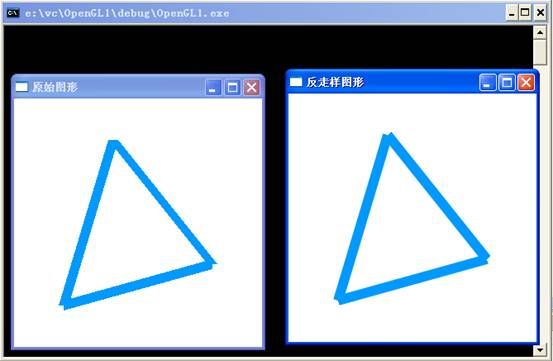
 glutCreateWindow("原始图形");
 glutDisplayFunc(Displayt);
    glutReshapeFunc(ChangeSize);
    Initial();

 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
 glutInitWindowPosition(300, 300);
 glutInitWindowSize(300, 300);
 glutCreateWindow("反走样图形");
 glutDisplayFunc(Displayw);
    glutReshapeFunc(ChangeSize);
 Initial();
 glutMainLoop();
}