第六章 图
一、内容小结
p.s.在数据结构之前,在离散数学课上也接触了图,当时接触的不深,但在DS课上加深了对图的应用的了解。
1.图的基本术语
①子图:相当于图是集合的话,子图就相当于是它的子集。其中有向图的也可以是无向图的子图。
②无向完全图:具有n(n-1)/2条边的无向图。有向完全图就是具有n(n-1)条弧的有向图。
③稀疏图和稠密图:少边或少弧则为稀疏图,反之则为稠密图。
④权和网:每条边上的权值为权。带权的图即为网。 ⑤入度和出度:与顶点相关联的边指向该结点则算一条入度,反向则算为一条出度。
⑥路径及路径长度:按着顶点的边顺序往下走为一条路径(可有向可序列),经过的弧或边的长度总和算该条路径长度。
⑦回路:第一个顶点和最后一个顶点重复的路径。 ⑧连通图:图中任意两个顶点均为连通的 ⑨连通分量:无向图中的极大连通子图。
2.查询算法
p.s.在迷宫案例中对DFS和BFS有了一定了解,而且在之后的区分也比较熟练了。
(1)DFS——深度优先算法:看了视频的案例,更快地理解了这个算法的原理。DFS是将一个一个顶点地进行遍历,若以下无可继续遍历,须原路返回再对顶点进行递归遍历,直至遍历完成。适合找所有路径(远一些)。
(2)BFS——广度优先算法:在每个顶点处往外画弧的形式遍历,效率较高。适合求最短路径。
二、学习心得
在增加“个人小测”的学习形式后,感觉自己对课堂内容的记忆更深刻了,应用起来也比较有思路,也能及时得到老师的指正,所以对我而言是比较有效的一种习题形式。
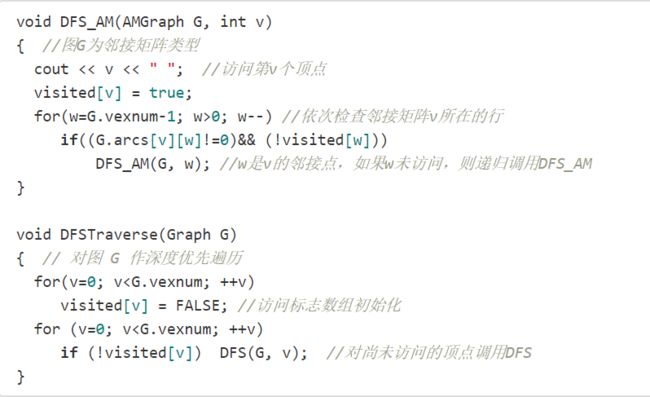
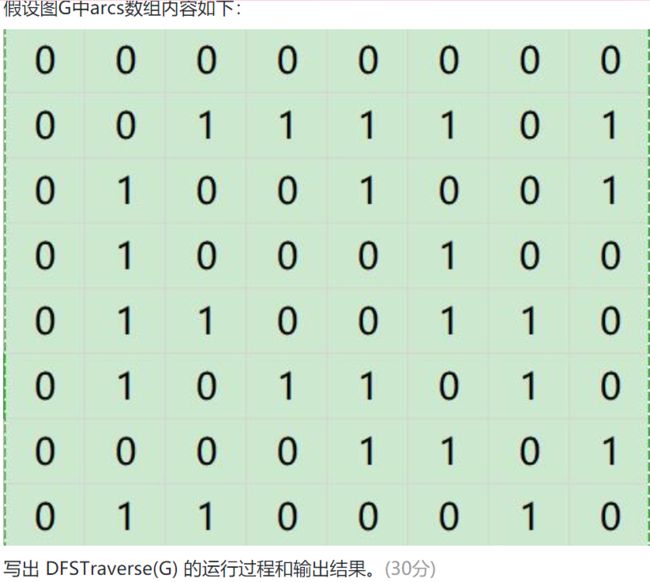
还有最近对于算法又接触了一层——写出流程。刚开始阅读DFS算法代码和数组内容:
由于时间比较赶,也就没太看清代码中的“陷阱”,导致自己从左向右的顺序来遍历导致出了错,下次会更细心些。
同时在这次算法练习中,学习到了大概的运行过程就是:在邻接矩阵中,递归调用DFS_AM的同时,使用了辅助数组visited[n]对访问结点不断进行更新赋值记录。就如以下:
①如果w(遍历的结点)未访问,则递归调用DFS_AM ,将visited数组中对应成员下标的visited值更新赋值为1;
②如果w已经访问,则不做变化,继续更新。
三、目标完成情况
上次目标完成情况:上次提到的认真学习课本内容,紧跟老师思路的方面上有在跟进中,虽然不是完全以优异的成绩完成各样测试,但在测试中都有得到不小的收获。虽然本章内容确实也如树一般知识点比较多,但在各种自主练习中逐渐找到了自己适应的学习方向,这一点还是让自己比较开心的。
本次目标:临近考试,各样知识点也需要重新回忆起来,掌握要点。所以希望自己能好好平衡好各科复习时间,将数据结构所学的关键代码题仔仔细细研究好敲一遍,增强自己的代码应用能力!更重要的,还是需要耐心和细心,尽量不要有畏难心理!