李航《统计学习方法》——第四章 朴素贝叶斯法

由于网上资料很多，这里就不再对算法原理进行推导，仅给出博主用Python实现的代码，供大家参考

适用问题：多类分类

基于贝叶斯定理和特征条件独立假设

常用的三个模型有：
- 高斯模型：处理特征是连续型变量的情况
- 多项式模型：最常见，要求特征是离散数据
- 伯努利模型：要求特征是离散的，且为布尔类型，即true和false，或者1和0

测试数据集：train.csv

实现代码（基于多项式模型）：

# encoding=utf-8

import pandas as pd
import numpy as np
import cv2
import time

from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score

# 二值化处理
def binaryzation(img):
    cv_img = img.astype(np.uint8)  # 类型转化成Numpy中的uint8型
    cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img)  # 大于50的值赋值为0,不然赋值为1
    return cv_img

# 训练，计算出先验概率和条件概率
def Train(trainset, train_labels):
    prior_probability = np.zeros(class_num)                         # 先验概率
    conditional_probability = np.zeros((class_num, feature_len, 2))   # 条件概率

    #  计算
    for i in range(len(train_labels)):
        img = binaryzation(trainset[i])     # 图片二值化，让每一个特征都只有0，1两种取值
        label = train_labels[i]

        prior_probability[label] += 1

        for j in range(feature_len):
            conditional_probability[label][j][img[j]] += 1

    # 将条件概率归到[1,10001]
    for i in range(class_num):
        for j in range(feature_len):

            # 经过二值化后图像只有0，1两种取值
            pix_0 = conditional_probability[i][j][0]
            pix_1 = conditional_probability[i][j][1]

            # 计算0，1像素点对应的条件概率
            probalility_0 = (float(pix_0)/float(pix_0+pix_1))*10000 + 1
            probalility_1 = (float(pix_1)/float(pix_0+pix_1))*10000 + 1

            conditional_probability[i][j][0] = probalility_0
            conditional_probability[i][j][1] = probalility_1

    return prior_probability, conditional_probability

# 计算概率
def calculate_probability(img, label):
    probability = int(prior_probability[label])

    for j in range(feature_len):
        probability *= int(conditional_probability[label][j][img[j]])

    return probability

# 预测
def Predict(testset, prior_probability, conditional_probability):
    predict = []

    # 对每个输入的x，将后验概率最大的类作为x的类输出
    for img in testset:

        img = binaryzation(img)  # 图像二值化

        max_label = 0
        max_probability = calculate_probability(img, 0)

        for j in range(1, class_num):
            probability = calculate_probability(img, j)

            if max_probability < probability:
                max_label = j
                max_probability = probability

        predict.append(max_label)

    return np.array(predict)


class_num = 10  # MINST数据集有10种labels，分别是“0,1,2,3,4,5,6,7,8,9”
feature_len = 784  # MINST数据集每个image有28*28=784个特征（pixels）

if __name__ == '__main__':

    print("Start read data")
    time_1 = time.time()

    raw_data = pd.read_csv('../data/train.csv', header=0)  # 读取csv数据
    data = raw_data.values

    features = data[::, 1::]
    labels = data[::, 0]

    # 避免过拟合，采用交叉验证，随机选取33%数据作为测试集，剩余为训练集
    train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)

    time_2 = time.time()
    print('read data cost %f seconds' % (time_2 - time_1))


    print('Start training')
    prior_probability, conditional_probability = Train(train_features, train_labels)
    time_3 = time.time()
    print('training cost %f seconds' % (time_3 - time_2))


    print('Start predicting')
    test_predict = Predict(test_features, prior_probability, conditional_probability)
    time_4 = time.time()
    print('predicting cost %f seconds' % (time_4 - time_3))


    score = accuracy_score(test_labels, test_predict)
print("The accruacy score is %f" % score)

代码可从这里naive_bayes/naive_bayes.py获取

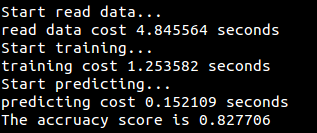
运行结果：




实现代码（基于多项式模型，用sklearn实现）：

# encoding=utf-8

import pandas as pd
import numpy as np
import time

from sklearn.naive_bayes import MultinomialNB

from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score


if __name__ == '__main__':

    print("Start read data...")
    time_1 = time.time()

    raw_data = pd.read_csv('../data/train.csv', header=0)  # 读取csv数据
    data = raw_data.values

    features = data[::, 1::]
    labels = data[::, 0]

    # 随机选取33%数据作为测试集，剩余为训练集
    train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)

    time_2 = time.time()
    print('read data cost %f seconds' % (time_2 - time_1))


    print('Start training...')
    clf = MultinomialNB(alpha=1.0) # 加入laplace平滑
    clf.fit(train_features, train_labels)
    time_3 = time.time()
    print('training cost %f seconds' % (time_3 - time_2))


    print('Start predicting...')
    test_predict = clf.predict(test_features)
    time_4 = time.time()
    print('predicting cost %f seconds' % (time_4 - time_3))


    score = accuracy_score(test_labels, test_predict)
print("The accruacy score is %f" % score)

代码可从这里naive_bayes/naive_bayes_sklearn.py获取

运行结果：