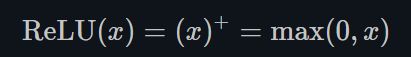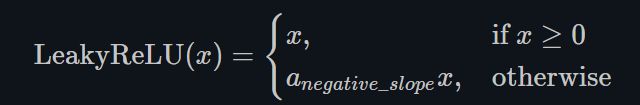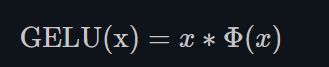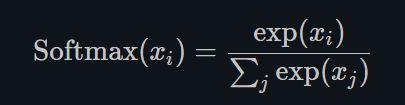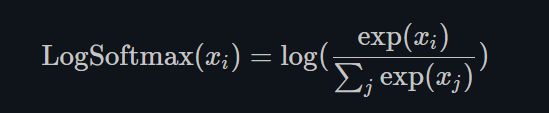PyTorch学习笔记(20) ——激活函数
0. 前言
本博客内容翻译自纽约大学数据科学中心在2020发布的《Deep Learning》课程的Activation Functions and Loss Functions部分.
废话不多说,下面直接开始吧 ^ . ^
1. 激活函数
本内容将回顾一些重要的激活函数以及其在PyTorch中的实现,它们来自各种各样的论文,并在一些任务上有着优异的表现~
- RReLU
torch.nn.RReLU()
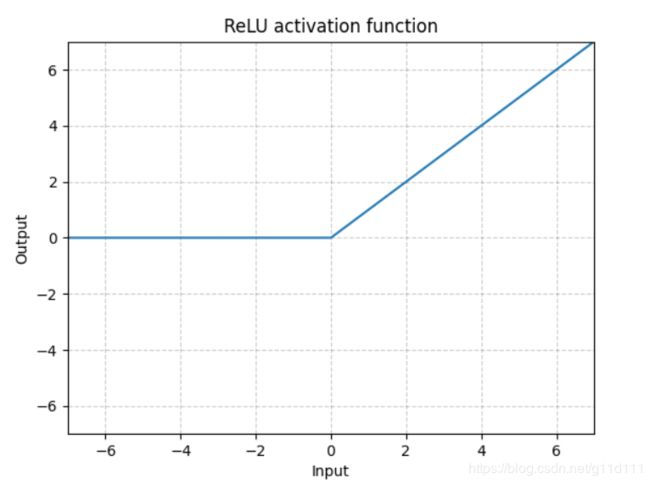
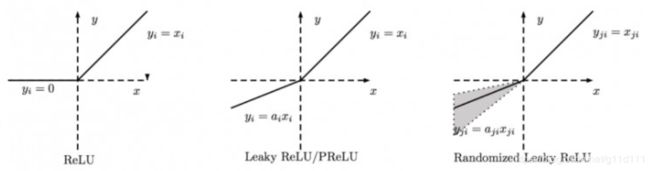
ReLU有很多变种, RReLU是Random ReLU的意思,定义如下:

对RReLU而言, a 是一个在给定范围内的随机变量(训练), 在推理时保持不变。同LeakyReLU不同的是,RReLU的a是可以learnable的参数,而LeakyReLU的a是固定的。
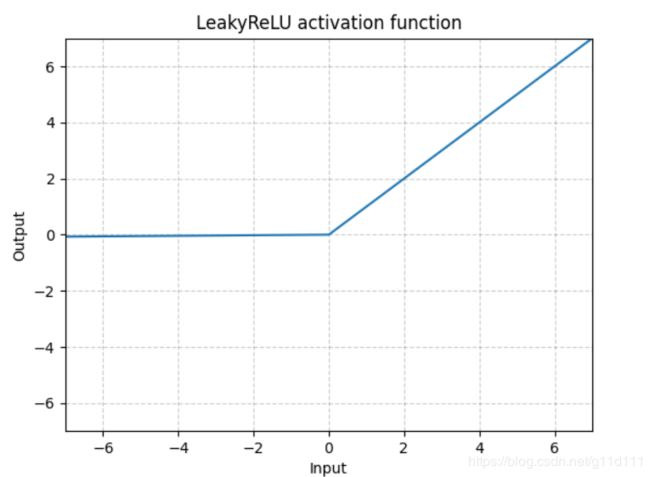
- LeakyReLU
torch.nn.LeakyReLU()
这里a是固定值,LeakyReLU的目的是为了避免激活函数不处理负值(小于0的部分梯度为0),通过使用negative slope,其使得网络可以在传递负值部分的梯度,让网络可以学习更多的信息,在一些应用中确实有较大的益处。
-
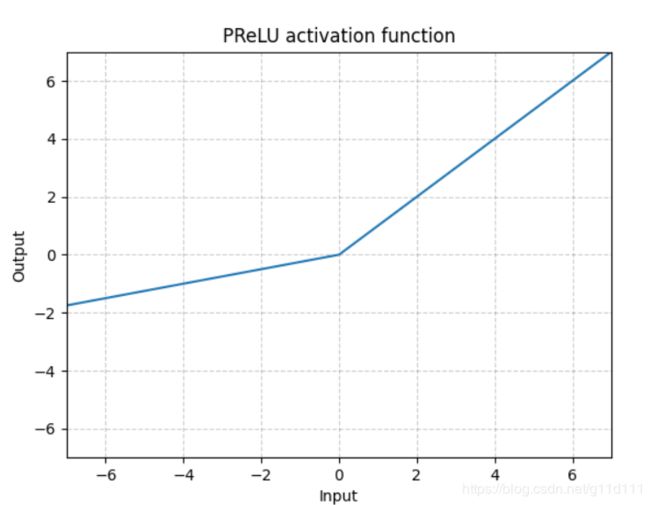
PReLU
torch.nn.PReLU()

不同于RReLU的a可以是随机的,PReLU中的a就是一个learnable的参数。
需要注意的是: 上述激活函数(即ReLU、LeakyReLU、PReLU)是 尺度不变(scale-invariant) 的。 -
Softplus
torch.nn.Softplus()
Sofrplus作为损失函数在StyleGAN1和2中都得到了使用,下面分别是其表达式和图解。
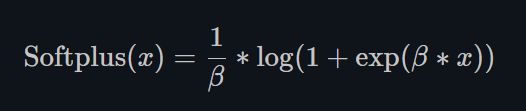

Softplus 是ReLU的光滑近似,可以有效的对输出都为正值的网络进行约束。
随着 β \beta β的增加,Softplus与ReLU越来越接近。
-
ELU
torch.nn.ELU()
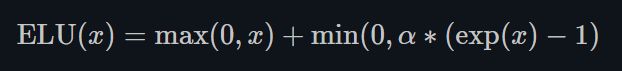
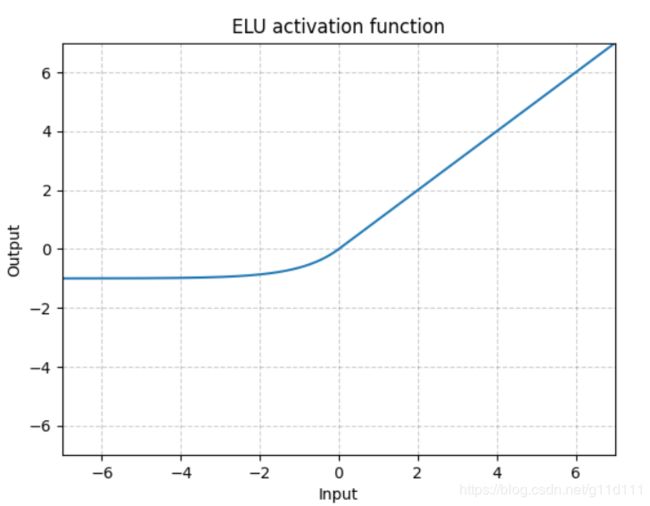
ELU不同于ReLU的点是,它可以输出小于0的值,使得系统的平均输出为0. 因此,ELU会使得模型收敛的更加快速,其变种(CELU, SELU)只是不同参数组合ELU。 -
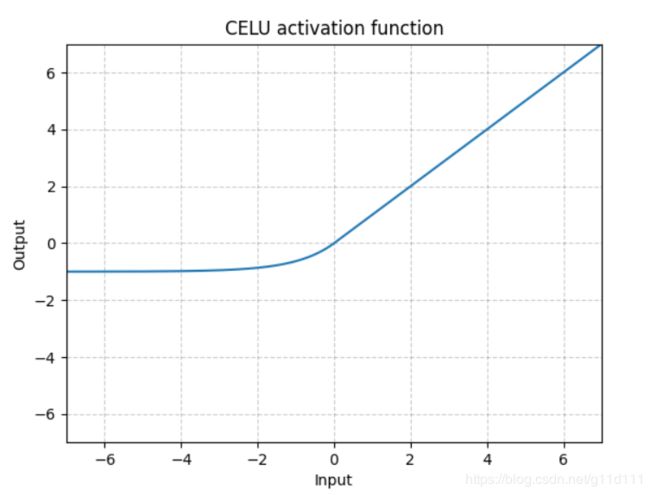
CELU
torch.nn.CELU()
跟ELU相比,CELU是将ELU中的 e x p ( x ) exp(x) exp(x)变为 e x p ( x / α ) exp(x/\alpha) exp(x/α).
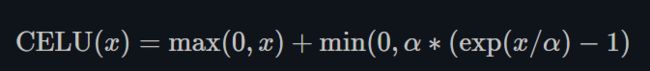
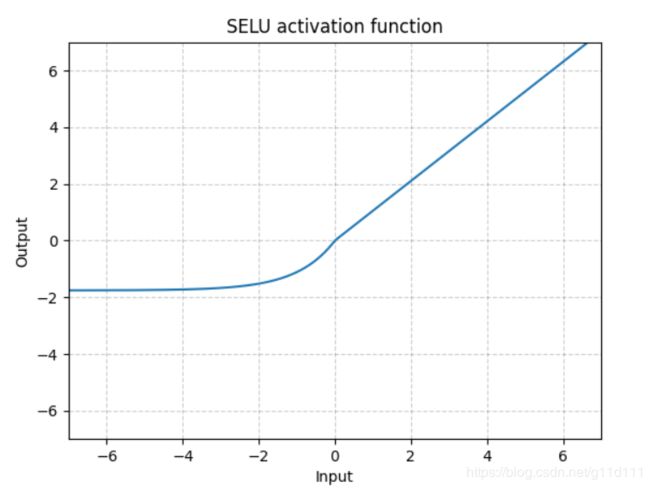
- SELU
torch.nn.SELU()
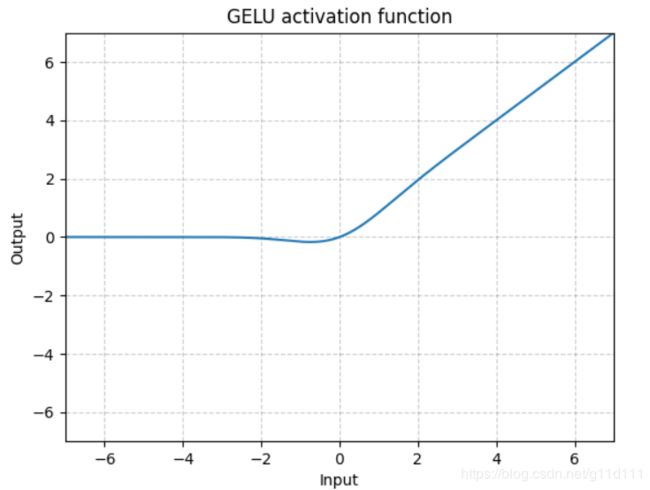
- GELU
torch.nn.GELU()
其中, Φ ( x ) \Phi(x) Φ(x)是高斯分布的累积分布函数 (Cumulative Distribution Function for Gaussian Distribution).
- ReLU6
torch.nn.ReLU6()
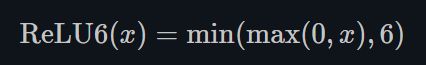

ReLU6是在ReLU的基础上,限制正值的上限为6. one-stage的目标检测网络SSD中用到这个激活函数啦~
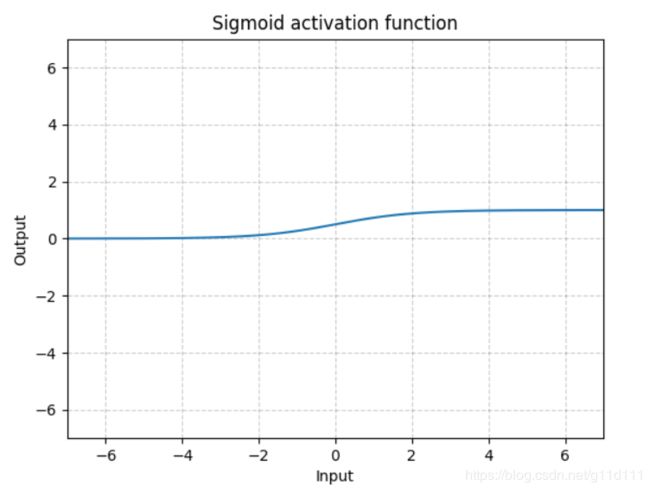
- Sigmoid
torch.nn.Sigmoid()
Sigmoid是将数据限制在0到1之间。而且,由于Sigmoid的最大的梯度为0.25,随着使用sigmoid的层越来越多,网络就变得很难收敛啦~
因此,对深度学习,ReLU及其变种被广泛使用来避免收敛困难的问题。
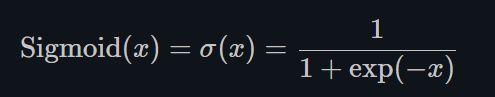
- Tanh
torch.nn.Tanh()
Tanh就是双曲正切,其输出的数值范围为-1到1. 其计算可以由三角函数计算,也可以由如下的表达式来得出:
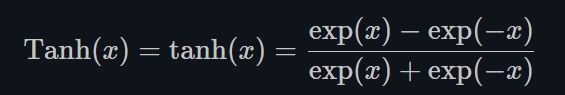

Tanh除了居中(-1到1)外,基本上与Sigmoid相同。这个函数的输出的均值大约为0。因此,模型收敛速度更快。注意,如果每个输入变量的平均值接近于0,那么收敛速度通常会更快,原理同Batch Norm。
-
Softsign
torch.nn.Softsign()
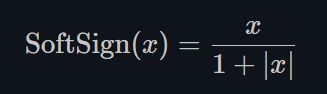

同Sigmoid有点类似,但是它比Sigmoid达到渐进线(asymptot n. [数] 渐近线)的速度更慢,有效的缓解了梯度消失的问题(gradient vanishing problem (to some extent).)。 -
Hardtanh
torch.nn.Hardtanh()
如下图所示,Hardtanh就是1个线性分段函数[-1, 1],但是用户可以调整下限min_val和上限max_val,使其范围扩大/缩小。

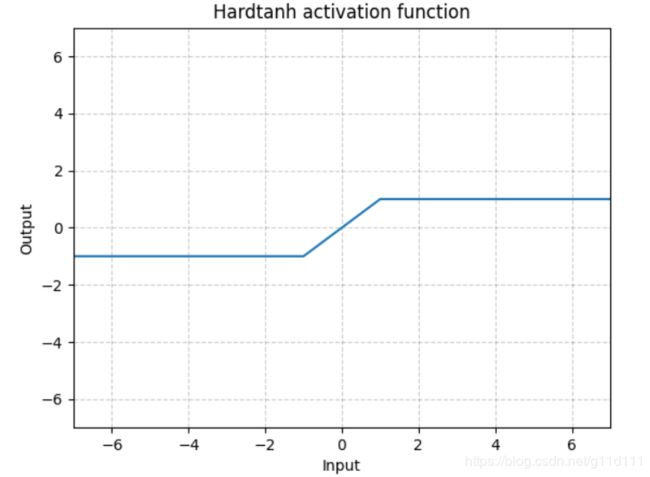
当权值保持在较小的范围内时,Hardtanh的工作效果出奇的好。
- Threshold
torch.nn.Threshold()
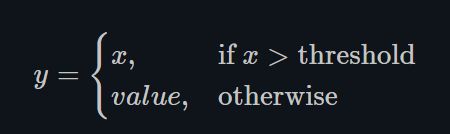
这种Threshold的方式现在很少使用,因为网络将不能传播梯度回来。这也是在60年代和70年代阻止人们使用反向传播的原因,因为当时的科研人员主要使用的是Binary的神经元,即输出只有0和1,脉冲信号。
-
Tanhshrink
torch.nn.Tanhshrink()

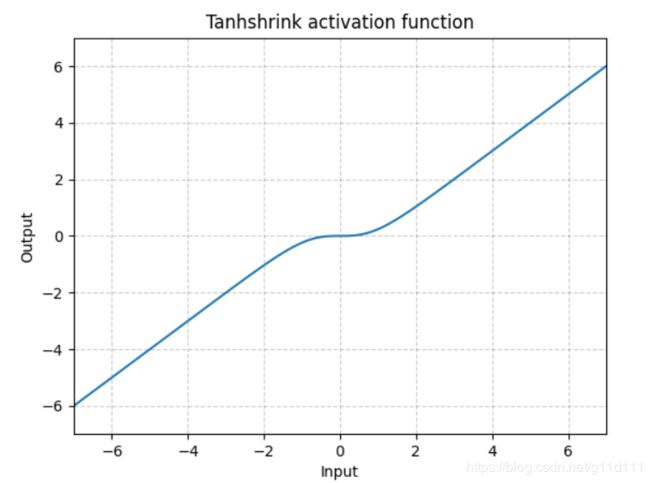
除了稀疏编码外,很少使用它来计算潜在变量(latent variable)的值。 -
Softshrink
torch.nn.Softshrink()
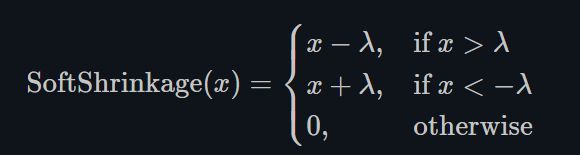
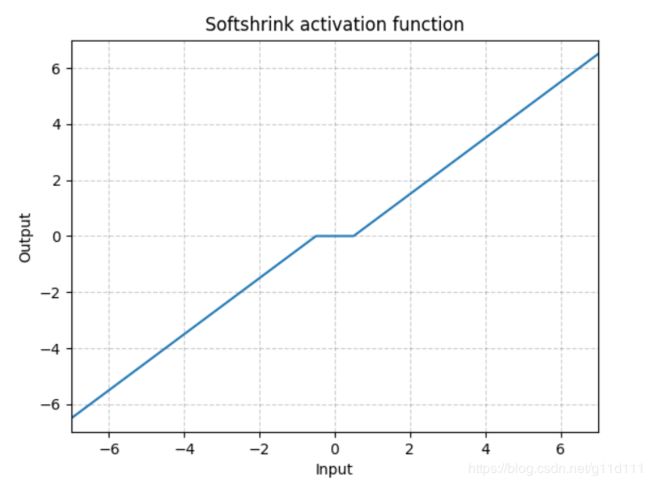
这种方式目前也不怎么常用,其目的是通过设置 λ \lambda λ,将靠近0的值直接强制归0,由于这种方式对小于0的部分没有约束,所以效果不太好~ -
Hardshrink
torch.nn.Hardshrink()
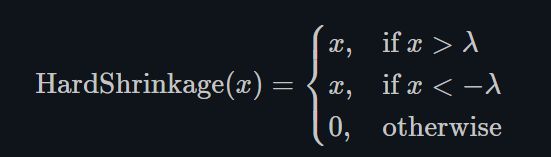

同Softshrink类似,除了稀疏编码以外,很少被使用。 -
LogSigmoid
torch.nn.LogSigmoid()
LogSigmoid是在Sigmoid基础上,wrap了一个对数函数。
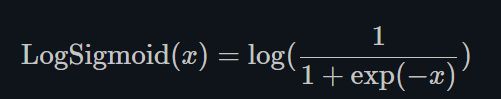
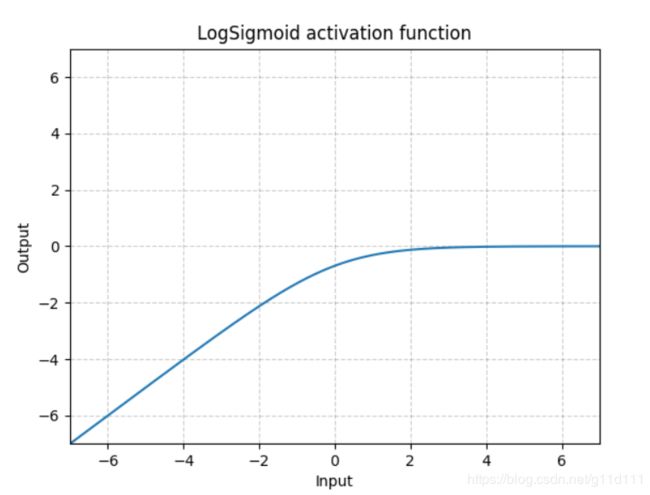
这种方式用作损失函数比较多,而几乎没人用它来做激活函数。
2. Q&A
① 对PReLU, RReLU这种变种来说,a是可学习或者固定的,有什么差别呢?
答: 固定a表示对负值区域,激活函数依然可以传递给网络固定的梯度。而让a是1个可学习的参数,意味着系统的非线性转换为线性映射。这可能对一些应用很有帮助: 比如实现一个不考虑边缘极性(regardless of the edge polarity)的边缘检测器。
② 想要的non-linearity的程度?
答: 理论上,我们可以将整个非线性函数以非常复杂的方式进行参数化: 如切比雪夫多项式ChebyShev等。参数化可以视为学习过程的一部分。在某种程度上,复杂程度取决于ChebyShev展开式的项数。
③ 与系统中有更多的单元相比,参数化的优点是什么?
答: 这主要取决于任务类型, 当你在做低维空间的回归任务时,参数化可能有用。但是,当你想要做类似image recognition这种高维空间的任务时,单调非线性的效果会更好。
简而言之,你可以参数任何你想要参数化的方程,但是这可能并不会带来很大收益,甚至有反效果。
④ 1 kink vs 2 kink
答: double kink (2 kink)表示当你放大输入为原来的2倍,那么你的输出将会与之前完全不同(不是原来的输出的2倍的关系)。这意味着网络具有很大的非线性。
而 one kink意味着输入你放大输入为原来的2倍,那么你的输出也会是原来的2倍,即非线性没有double kink那么强。
⑤ 带kinks和带光滑非线性的激活函数,哪个更好?
答: 这与规模等变有关。如果带有hard kinks,这意味着当你对输入数据乘以2,那么你得到的输出应该也会等比放大2倍。而如果你有个光滑的变换过程(通过激活函数赋予),当你对输入乘以100,那么你的输出看起来会有个hard kink,这是因为平滑的部分缩小了100倍。
而当你对输入除以100,那么kink就变得非常光滑了。因此,通过对输入的scale进行缩小或者放大,你可以修正激活单元的行为。