PyTorch学习笔记(21) ——损失函数

0. 前言

本博客内容翻译自纽约大学数据科学中心在2020发布的《Deep Learning》课程的Activation Functions and Loss Functions
部分.

废话不多说，下面直接开始吧 ^ . ^

1. 损失函数

本文是PyTorch学习笔记(20)——激活函数的姊妹篇。

PyTorch实现了许多损失函数，这些我们将介绍其中的一些。

• nn.MSELoss()

MSELoss也叫做L2 loss, 这个函数的作用是: 对输入x和目标y进行element-wise的计算均方误差(mean squared error).

$$(x_n-y_n{)}^2$$

在PyTorch中，MSELoss有2种方式: 一种是reduce，另一种是unreduce。

其中，unreduce的含义是将mini-batch中的每个样本的loss分别保存，即以一个 向量(Vector) 的方式保存；而reduce是指将mini-batch的每个样本的loss按照一定的方式进行平均，最后只保存一个标量(Scalar)。

① reduction=‘None’ (对batch中的每个样本保存其自己的loss)

② reduction=‘mean’ or ‘sum’ (求平均或者求和)

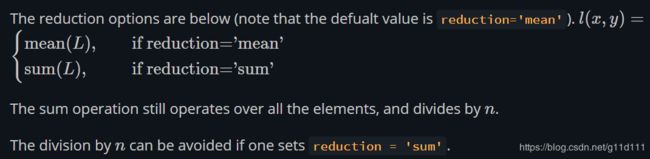
如果我们在计算机视觉任务中使用reduce的MSE (L2 Loss), 这通常意味着我们最后得到的结果会有或多或少的模糊：因为你对每一项的loss都进行求和或者求平均了，那么loss将很难反映出图像/视频中的每个部分对结果的影响。

而我们如果在计算机视觉任务中使用L1 Loss，通常会得到更锐利的结果。

• nn.L1Loss()
  This measures the mean absolute error (MAE) betwen each element in the input xx and target yy (or the actual output and desired output).
  L1Loss衡量的是输入x和目标y（或者实际输出和理想输出）的平均绝对值误差(mean absolute error, MAE)。

$$|x_n-y_n|$$

同MSELoss类似，L1Loss也有unreduce和reduce2种，其方式与MSELoss无差别。

在实际使用中，L1 loss相比L2 loss对离群点(outliers)和噪声(noise)有着更强的鲁棒性(L1 loss is more robust against outliers and noise compared to L2 loss)。这是因为L2 loss对离群点和噪声计算平方，所以使得损失函数对于这些离群点和噪声更加的敏感。

但是，L1 loss的问题是其在一些地方不可微分，这使得一些部分的导数为0，所以为了避免L1 loss的hard margin问题，Smoot和L1Loss被提出，用于缓解梯度问题。

• nn.SmoothL1Loss()

这个函数根据目标输出和给定输出的相差情况(<1, >=1)来分别使用不同的损失函数计算公式:

$$z_i=\{\begin{array}{l}0.5(x_i-y_i{)}^2,if|x_i-y_i|<1\\ |x_i-y_i|-0.5,otherwise\end{array}$$

该损失函数在FAIR的大神Ross Girshick的目标检测经典网络: Fast R-CNN中大放异彩，这种光滑的L1 Loss也被称作Huber Loss。

相对MSELoss(L2 Loss), Smooth L1 Loss对于离群点和噪声没有那么敏感。这个损失函数经常用于一些计算机视觉中一些需要避免/有效防止离群点的应用。

当然，Smooth L1 Loss也有一些问题：它对损失函数进行了缩放, 缩放系数为0.5.

• nn.NLLLoss()

NLLLoss被用于训练N分类任务，其含义是负对数似然损失函数（negative log likelihood loss）。

$$-w_{y_n}\ast x_{n,y_n}$$
需要注意的是，在数学上，NLLLoss的输入应该是log似然估计，但是PyTorch并没有强制用户这样做。

同样的，NLLLoss也分为reduce和unreduce，其形似分别如下：

① unreduce

② reduce

注意，$w_{n,y_n}$表示第n个样本对应于$y_n$类的权值，这是1个标量。

NLLLoss有一个optional的参数weight, 这个参数是1个1D Tensor，其长度与类别数一致。传入weight的方式对处理不平衡的训练集有很大的好处。

• nn.CrossEntropyLoss()

CrossEntropyLoss是将nn.LogSoftmax和nn.NLLLoss合二为一的损失函数。这种结合使得正确类的得分变得尽可能的高。

将二者合并为一个新的损失函数的原因是为了梯度计算的数值稳定性(numerical stability of gradient computation). 因为当数据过softmax后，其靠近0或者1的值的梯度就几乎不存在了。而Softmax后靠近0的值，在LogSoftmax里接近负无穷；Softmax后靠近1的值，在LogSoftmax里接近0. 这会造成数值问题。

但是当这两个函数结合在一起时，我们可以得到饱和的梯度，所以我们在最后能够得到一个合理的梯度。

每个类的输入应该是unnormalized。

损失函数可以定义为:

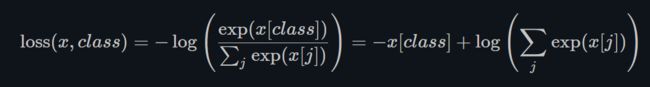
如果指定了weight参数，其形式为:

注意，这里不再分reduce和unreduce了，损失函数的计算是reduce的(reduction==‘mean’).

交叉熵的物理含义与KL散度（Kullback-Leibler Divergence）有关, KL散度常常被用于衡量2个分布的相似性。

这里，我们有目标分布(one-hot) $q$和神经网络预测分布$p$, 那么数学上, $$H(p,q)=-\sum _{i}p(x_i)log(q(x_i))$$ 其解析表达式为:
$$H(p,q)=H(p)+D_{KL}(p||q)$$

这里，$H(p,q)$就是2个分布的交叉熵，$H(p)=-{\sum }_{i}p(x_i)log(p(x_i))$是熵(Entropy)，而$D_{KL}(p||q)={\sum }_{i}p(x_i)log\frac{p(x_i)}{q(x_i)}$就是KL散度。

• nn.AdaptiveLogSoftmaxWithLoss()

这个是对有非常多的类(比如上百万个类)的Softmax的高效实现。它被用于提升计算的效率。详细的细节请参考FAIR的Edouard Grave, Armand Joulin等人于2016年写的论文Efficient softmax approximation for GPUs

• Binary Cross Entropy (BCE) Lossnn.BCELoss()

二分类的交叉熵，是交叉熵的特殊情况。BCE经常被用于衡量重建误差: 比如auto-encoder。需要注意的是，因为这里我们认为$x$和$y$都是概率，所以BCE用到数据需要规则化到[0, 1]之间。

• Kullback-Leibler Divergence Loss nn.KLDivLoss()

KLDivLoss对one-hot label的情况比较常用。它与BCELoss一样，也把$x$和$y$视为概率分布。它的缺点是没有与Softmax或LogSoftmax合并，因此会存在数值稳定性问题。

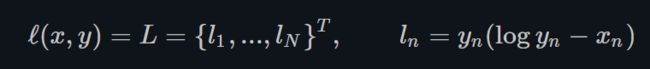
• BCE Loss with Logitsnn.BCEWithLogitsLoss()

可以看出，相比BCE Loss，我们对log里的$x$加上了一个激活函数$\sigma$ = Sigmoid. 其目的是确保输入到BCE 里面的数据都被归一化到0和1之间。

• Margin Ranking Loss nn.MarginRankingLoss()

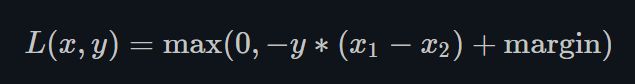
Margin loss是1类非常重要的损失函数。如果你有2个输入，那么Margin loss的目的是让其中的1个输入至少比另1个输入大margin (margin是个标量)。

如上面的式子, $y$只取 $-1,1$. 让我们想象$x_1$和$x_2$是两个类别的分数。你的目的是想让正确类别的得分比错误类别的得分至少高出margin。

与Hinge Loss类似，如果$y\ast (x_1-x_2)$大于margin，那么根据Margin Loss的定义，loss的值为0. 而如果小于margin，那么随着$y\ast (x_1-x_2)$的减小，Margin Loss线性增加。

以分类任务为例，$x_1$应该是正确答案的得分而$x_2$是得分最高的错误答案，$y=1$.

• Triplet Margin Loss nn.TripletMarginLoss()
  
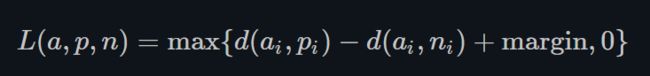
  Triplet margin loss是用于度量样本之间的相似性的指标。
  举个例子，你把同属1类的2张不同图片喂入神经网络中(如同属花类的月季，海棠)来得到2个feature vector。你想让同一类的feature vector尽可能的接近。

类似地，当你将不同类的图片喂入神经网络，得到的feature vector，你想让这2个feature vector的距离越远越好。

而Triplet Margin Loss的目的就是让 “类内距离最小，类间距离最大”。

Triplet Margin Loss公式中的$a$表示anchor, $p$表示positive, 表示与anchor同类的样本；$n$表示negtive，表示与anchor不同类的样本。

TripleLet Loss的应用我知道的是FaceNet，用于人脸识别的网络，大概是16年的样子发出来的。

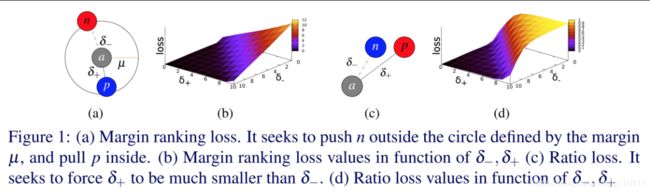
Triplet Margin Loss最初被用于谷歌的image search系统。其原理很简单:

At that time, you would type a query into Google and it would encode that query into a vector. It would then compare that vector to a bunch of vectors from images that were previously indexed. Google would then
retrieve the images that were the closest to your vector.

• Soft Margin Loss nn.SoftMarginLoss()
  
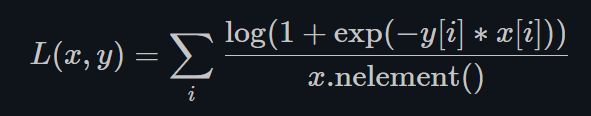
  Soft Margin Loss创建了优化2分类逻辑损失的标准（在输入Tensor $x$ 和 目标Tensor $y$之间），$y$的取值同Margin，也是-1和1。

其特点是:

① Margin Loss的softmax版本. 损失函数的目的是让$exp(-y[i]\ast x[i])$在$x[i]$和$y[i]$对应上的时候(同属1类)的情况下loss更小。因为指数函数的性质:

② Soft Margin Loss的目的与Margin Loss一样，即让类内距离变近，类间距离变远。但不同于Hard Margin，Soft Margin Loss在损失函数中加入了连续性，指数衰减的特征，使得损失函数变得更加光滑，因此其对应的梯度范围也比Hard Margin的Loss更大。理论上会使得模型收敛更加容易。

• Multi-Class Hinge Loss nn.MultiLabelMarginLoss()

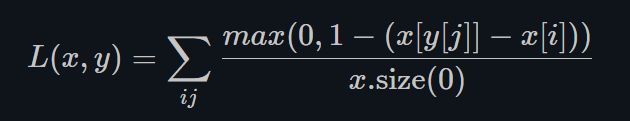
多分类Hinge Loss也是基于margin的loss，它允许输入拥有不同数量的target。

$x[y[j]]$表示正确的类得分，$x[i]$表示错误的类的得分，损失函数的设计目的是让2者相差越大越好（即损失函数会越来越小）。

• Hinge Embedding Loss nn.HingeEmbeddingLoss()

Hinge Embedding Loss被用于在半监督学习(semi-supervised learning)中度量输入的相似性。

它将相似的输入拉近(pull together)，将不相似的输入拉远(pull away). 标签$y$表明得分是否需要向某个特定方向发展（The $y$ variable indicates whether the pair of scores need to go in a certain direction）。

• Cosine Embedding Loss nn.CosineEmbeddingLoss()

Cosine Embedding Loss的目的是用cosine distance来衡量输入的相似性。在学习非线性embeddings或半监督学习中被广泛使用。

① 首先，我们用1减去2个向量的夹角的余弦来表示规则化的欧式距离(normalized Euclidean distance)。

② 这样做的好处是，无论何时你有两个向量你想让它们的距离尽可能大，很容易让网络通过让向量很长来实现这一点。而这不是最优的。你不希望使向量变大/长，而是应该通过让向量向正确的方向旋转，这样就可以对向量进行标准化，并计算出标准化的欧几里得距离。

③ 理想情况下，Cosine Embedding Loss可以使得向量Vector尽可能的对齐。而Cosine Embedding Loss也可能会使得余弦值小于特定的margin（margin通常是一个small positive value）。

④ 以地球为例，在赤道附近的区域要远大于高纬度地区的区域。我们对地球上的点进行归一化，你想保证的是语义上相近的样本依然相近，而语义上不相近的样本相互正交。注意，你不想让不相近的样本相反，这是因为只有2个完全相反点存在（极点）。而因为赤道上有很大的取值范围，所以你要让Margin为正这样你就能利用所有这些面积。

• Connectionist Temporal Classification (CTC) Loss nn.CTCLoss()

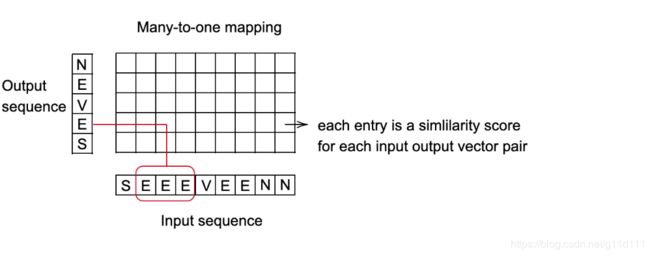
CTC Loss在音频处理中得到非常广泛的使用，其目的是度量连续的时间序列和目标序列的差异。

① CTC Loss对输入的可能排列和target的概率求和，输出1个loss值，这个值对任何输入节点都是可微的。

② 这种输入和目标align的方式被称为"mang-to-one", 这限制了target sequence的长度，使得target sequence的长度必须小于等于input length。

③ 当网络的输出是对应于类别的分数的向量序列时，它非常有用。

应用案例: 语音识别

• 目标：每10毫秒预测一个单词的发音。
• 每个单词都由一连串的声音表示。
• 根据说话人的语速，不同长度的声音可能会映射到同一个单词上。
• 找到输入sequence和输出sequence的最佳映射关系。一个比较好的方法是使用动态规划来找到最优代价路径。

语音识别的CTC Loss

Many-to-one 映射过程示意图